Конспект по темі: "Чотирикутники"

Підсумковий урок
по темі: "Чотирикутники

Мета: повторити і узагальнити знання учнів з теми "Чотирикутники, розвивати логічне мислення, просторову уяву, вміння знаходити вихід із нестандартної ситуації, виховувати увагу, акуратність, самостійність, потяг до знань.

Хід уроку:

1. Перевірка домашньої роботи.

Фронтально перевіряю д/з, учні - консультанти доповідають про
виконання д/з у класі.

2. Актуалізація опорних знань.

Учні класу об'єднані в домашні групи, кожна з яких захищає
певний вид чотирикутника.                                                           

Вчитель: Сьогодні ми проведемо підсумковий урок із теми
"Чотирикутники".Спочатку повторимо всі види опуклих
чотирикутників, їхні властивості і ознаки.
(Повторення проводимо у формі "Мікрофон")

Вчитель: У Математики - цариці є дві доньки яснолиці.

І красиві, і вродливі, і розумні, й справедливі.
Ой, забула, як їх звуть ...
Що робити, як тут буть?
Ви мені допоможіть і швиденько підкажіть!

Учні: Алгебра і Геометрія.

Вчитель: У геометрії сестриці

Завжди лад був у світлиці.
Але якось (ах! та ох!)
Стався там переполох.

Паралелограм:

Тихіше!

Розбалакалися як!

І Я у царстві чотирикутників не будяк.

Учень:

Бачимо що ти не будяк!
Та ж ти нам знайомий!
Підкажіть колеги:
Як він зветься і чому?
Дать означення йому.

Учні: Це - паралелограм.

1. Паралелограм - це чотирикутник, протилежні сторони
   попарно паралельні.
2. У паралелограма протилежні сторони рівні.
3. Протилежні кути рівні.
4. Діагоналі точкою перетину діляться пополам.

Паралелограм:

Паралельних маю більше,
Тож від чотирикутників
Я не гірший!

Прямокутник:

А про мене ви забули?
Чи, можливо, і не чули?

Учні: Це - прямокутник.

1. Прямокутник - це паралелограм, у якого всі кути прямі.
2. У прямокутника діагоналі рівні.
3. Діагоналі точкою перетину діляться пополам.
4. Протилежні кути рівні.
5. Протилежні сторони рівні.
6.                              Його площа - 8 = ахЬ
7. Його периметр - Р — 2 х (а + Ь)

Ромб: Незвичайну маю форму
Та вкладаюся у норму!

Учні: Це - ромб.

1. Ромб - це паралелограм, у якого всі сторони рівні.
2. У ромба протилежні кути рівні.
3. Діагоналі перпендикулярні.
4. Діагоналі точкою перетину діляться пополам.
5. Діагоналі ділять кути пополам
6. Його периметр - Р = 4 X а

Квадрат: Я для всіх вас старший брат. Знаєте хто я?

Учні: Квадрат.

Вчитель: Дайте шану і йому.

Старший зве себе. Чому?

Учні:

1. Квадрат - це прямокутник, у якого всі сторони рівнв.
2. Квадрат - це ромб, у якого всі кути рівні.
3. Квадрат - це паралелограм, у якого всі сторони рівні і всі кути
   прямі.
4. У квадрата діагоналі перпендикулярні.
5. Всі кути рівні.
6. Діагоналі рівні.
7. Діагоналі точкою перетину діляться пополам.
8. Його площа - 8 — а"
9. Його периметр - Р = 4а
   3. Робота "експертних груп".

( Учні однієї групи задають питання учням інших груп.)
1 .Довести властивість діагоналей ромба. (Діагоналі перпендикулярні)

2.Довести, що діагоналі прямокутника рівні.

3.Довести, що діагоналі паралелограма точкою перетину діляться
пополам.

4.Діагоналі квадрата є бісектрисами його кутів.

4.   Розв'язування задач і вправ.

Ви, фігури, не сваріться
А швиденько помиріться
Йде війною на нас цар -

чужоземний господар.
І таку він має вдачу;
Любить всім давать задачі.
Хто розв'яже - тих милує,
А хто ні - той пожалкує.
Роздаю кожній групі завдання для роботи в групі.

І група.

Периметр прямокутника дорівнює 32 см, а одна із його сторін
на 8см довша за іншу. Знайти площу прямокутника.

1. Дано: АВСБ - ромб; ^ СОК = 70°.
   Знайти: АВС.

8

2. група:

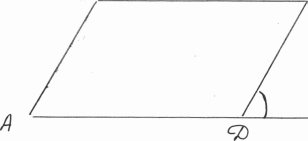
1.Діагональ паралелограма утворює з його сторонами кути 35° і
45°. Знайти кути паралелограма.

1.Сторони прямокутника відносяться, як 7 : 3, а його периметр
дорівнює 60см. Знайти площу прямокутника.

3. група:

І.Одна із сторін паралелограма втричі довша за іншу. Знайти
сторони паралелограма, якщо відомо, що його периметр дорівнює
48см.

2.Сума двох кутів ромба дорівнює 240°. Знайти кути ромба.

IV група:

1. Одна із сторін прямокутника на Зсм коротша за другу. Знайти
   сторони прямокутника, якщо його периметр дорівнює 26см.
2. У ромбі АВСО точка О - точка перетину діагоналей. Відомо,
   що кут АВО дорівнює 40°. Знайти кути ромба

(Розв'язок однієї із задач учні коментують.)

Вчитель: Впоралися, як годиться,
Та цареві не сидиться.
Таку погану має вдачу,
Що прислав ще нам задачу.

Задача:

1. Бісектриса тупого кута паралелограма ділить протилежну
сторону навпіл. Менша сторона паралелограма дорівнює 4см. Знайти
периметр паралелограма.
(Колективне розв'язування задачі.)

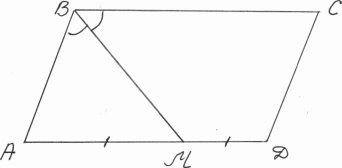
а) Що скажете про АВМ?

и А = х°, то /АВМ = 90° - §-)

б) Як знайти АМВ?

(180°-(х + 90°-!)= ¹⁸⁰°- І - 90° - 90° - §)

в) Який вид а АВМ?
(рівнобедрений)

г) Який висновок з цього випливає?
(АВ = АМ = 4см.)

д) Чому дорівнює сторона АО?
(АО = 2x4 = 8см.)

е) Чому дорівнює периметр паралелограма?
(Р= 2 (4 + 8) = 24см.)

Відповідь: 24см.

Домашнє завдання.

1. Вправа: 128, 129*, 1116; ст.38 - 39
2. Зобразити себе за допомогою геометричних фігури.

Підсумок уроку.

Про ваш емоційний стан я можу судити з виразу вашого
обличчя. А тепер хочу почути, що вам сподобалося на
сьогоднішньому уроці, а що можна змінити на краще.

•      Що ми робили на уроці?
•      Що нового навчилися?
•      Навіщо це робили?

•      Чи досягли очікуваних результатів?
•      Чи сподобався вам спосіб проведення сьогоднішнього уроку?
•      Що сподобалось особливо під час уроку? Що не сподобалось?
•      Що могло бути організовано краще, корисніше?