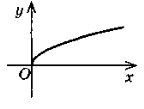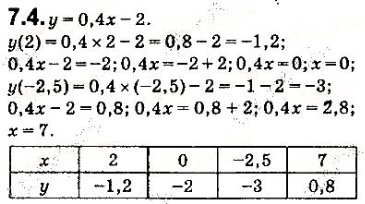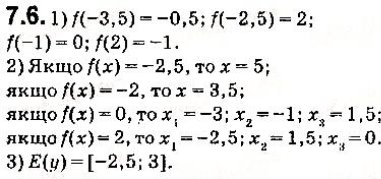Конспект року 24. "Функція". Тема "Квадратична функція"
Розширити поняття «функція», систематизувати знання учнів про зміст понять: функція, аргумент, область визначення та область значень. Розвивати вміння відтворювати означення вивчених понять, а також розв'язувати задачі на знаходження значень функції за значенням аргументу, область визначення та область значень заданих функцій.
Урок № 24
Алгебра 9 клас
Дата:
За підручником «Алгебра», 9 клас авторів А.Г. Мерзляк, В.Б.Полонська,
М.С. Якір, «Гімназія», 2017 рік.
Тема уроку. Функція.
Мета уроку:
Навчальна: Розширити поняття «функція», систематизувати знання учнів про зміст понять: функція, аргумент, область визначення та область значень. Розвивати вміння відтворювати означення вивчених понять, а також розв'язувати задачі на знаходження значень функції за значенням аргументу, область визначення та область значень заданих функцій.
Розвивальна: Розвивати вміння побудови та читання графіків функцій, математичну мову.
Виховна: Виховувати потяг до нових знань, самостійність, повагу до думки іншого, охайність у записах, побудові графіків.
Тип уроку. Формування знань та вмінь.
Обладнання. Підручник, конспект, презентація, проектор, екран, комп’ютер.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу, перевіряє наявність креслярських приладів, при потребі надає їх учням.
II. Перевірка домашнього завдання
Учитель перевіряє правильність виконання і наявність домашнього завдання в учнів.
III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності
Поняття функції виникло в математиці порівняно недавно. Первинною математичною моделлю є функція, тому функції, їх властивості та графіки, як у явній, так і в неявній формі, складають одну із основних понять шкільного курсу математики, тому ми в 9 класі продовжимо вивчати функцію. Починаючи з XVII століття одним із найважливіших понять є поняття функції. Воно відіграло і понині грає велику роль у пізнанні реального світу. Шлях до появи поняття функції заклали в 17 столітті французькі вчені Франсуа Вієт і Рене Декарт; вони розробили єдину буквену математичну символіку, яка незабаром отримала загальне визнання. Поняття функція було введено в кінці XVII ст.(functio в перекладі «виконання»). Термін «функція» ввів Лейбніц в 1694р. На сторінках 65 – 68 підручника ви можете прочитати «З історії виникнення функції».
IV. Актуалізація опорних знань та вмінь
Усні вправи
- Виконайте дії:
1) -1,73 – 2,77; 2) -4,5 ∙ 0,4; 3) 43 : 23;
4) -0,6 ∙ (-0,3) - 0,2; 5) (3,1 + 0,09)0 : ![]() ; 6) (-7 + 2,5) : 1,5.
; 6) (-7 + 2,5) : 1,5.
- Знайдіть значення виразу:
1) 3 – 2а при а = -3; 2) 2х - 5 при х = 3;
3) ![]() х +
х + ![]() у при x = 24, y = -16.
у при x = 24, y = -16.
-
При яких значеннях змінної існує вираз:
1) х + 9; 2)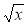 + 9; 3)
+ 9; 3) 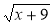 ; 4)
; 4) 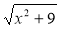 ;
;
5)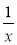 + 9; 6)
+ 9; 6) 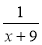 ; 7)
; 7) 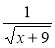 ?
?
V. Систематизація та доповнення знань
|
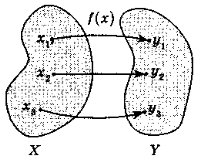
Функція — це правило, за допомогою якого за кожним значенням незалежної змінної з множини Х можна знайти єдине значення залежної змінної з множиниY. |
||||||||||||||||||||||||||||||||||||||
|
|
Позначається: y = f(x), де х — аргумент (незалежна змінна); у — функція, значення функції (залежна змінна); f(x0) — значення функції в точці х0. |
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
Функцію можна задати одним із способів:
|
||||||||||||||||||||||||||||||||||||||
|
|
Область визначення функції D(f) або D(у) — це множина всіх значень, яких набуває аргумент. |
|||||||||||||||||||||||||||||||||||||
|
|
Як знайти область визначення функції y = f(x)
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
VI. Відпрацювання навичок. Удосконалення вмінь Усні вправи
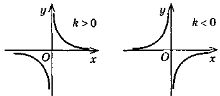
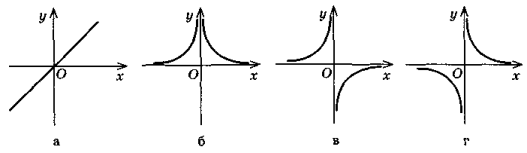
Функція задана формулою f (x) = 1) Що означають записи f (2) і f (-8)? 2) Чому дорівнюють значення виразів f (2) і f (-8) ? 3) Яка область визначення функції? 4) Який із даних графіків є графіком цієї функції?
Письмові вправи Колективно
Робота в парі
Пара, яка справилася першою презентує розв'язок № 7.4 виконати самостійно. Звіритись за презентацією
Робота в групі
VII. Підсумки уроку Вправа «Вільний мікрофон». Відповідають бажаючі, підходять до мікрофона і говорять. 1. Що таке функція? 2. Як позначають той факт, що змінна y функціонально залежить від змінної x? 3. Що називають аргументом функції? 4. Що називають областю визначення функції? 5. Що називають значенням функції? 6. Що називають областю значень функції? 7. Що треба вказати, щоб функція вважалася заданою? 8. Які способи задання функції ви знаєте? 9. Що вважають областю визначення функції, якщо її задано формулою та при цьому не вказано область визначення? Тестові завдання
а) рівнянням у = f(x); б) областю визначення; в) аргументом; г) графіком.
а) аргумент; б) область визначення; в) функція; г) область значення функції.
3. Знайти область визначення функції у =
а) [8; +
в) (8; +
4. Обчислити значення функції f (х) = а) 25 ; б) 1 ; в) 0 ; г) інша відповідь 5.Множина всіх точок з координатами (x; f(x)), де y = f(x) — задана функція, це: а) точка; б) лінія; в) f(x); г) графік функції y = f(x). Відповіді:
Звіритись за слайдом VIII. Рефлексія На уроці я
§ 2, п. 7 - опрацювати, правила повторити; №№ 7.2; 7.5; 7.7 - письмово.Ст. 65 – 68 – відомості з історії функції прочитати. |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||


про публікацію авторської розробки
Додати розробку