Конспект учня на час карантину з теми:" Скалярний добуток"

Число за розкладом

Класна робота

[все письмово]

№41.19

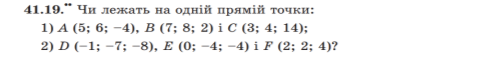
Розв’язання до 1:

Якщо вектори АВ і АС колінеарні ( обов’язково, щоб одна з точок у векторів була спільною) , то точки лежать на одній прямій.

АВ( 7-5; 8-6; 2+4) = АВ(2;2;6)

АС(3 - 1; 4 – 6; 14 +4) = АС (2; -2; 6)

Якщо , то вектори колінеарні.

Перевіряємо  . Оскільки рівності не рівні, то вектори не колінеарні. Отже точки не лежать на одній прямій.

Завдання 2 самостійно! (д.з)

Тема: Скалярний добуток векторів

Скалярним добутком векторів і називають число .

Приклад 1. Знайти скалярний добуток векторів та .

Розв’язання:

Знайдемо скалярний добуток рівних векторів. Нехай дано вектор . Тоді:

Добуток записують  і називають скалярним квадратом вектора.

Скалярний квадрат вектора дорівнює квадрату його модуля:

.

Властивості скалярного добутку:

Для будь-яких векторів і будь-якого числа :

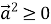1. , до того ж 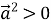, якщо .
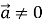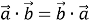2. -- переставна властивість.
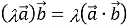3. -- сполучна властивість.
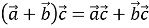4. -- розподільна властивість.

Кутом між двома ненульовими векторами, що не мають спільного початку називають кут між векторами, що дорівнюють даним і мають спільний початок.

 Кут між співнапрямленими векторами = 0⁰,

кут між протилежно напрямленими векторами = 180.

Скалярним добутком двох ненульових векторів називається число, яке дорівнює добутку числових значень довжин цих векторів і косинус кута між векторами:

, де =.

Наслідок 1. Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.

Наслідок 2. Якщо скалярний добуток векторів дорівнює нулю, то вони перпендикулярні.

Кут між ненульовими векторами можна визначити за формулою

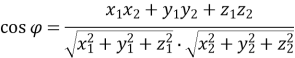
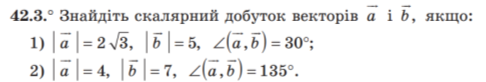
1. Самостійно (д.з)
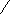
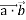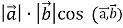2. = = 4 * 7 * cos135⁰= 28 * 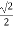= 14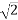

За формулою cos(

cos135⁰  = cos (180⁰ – 45⁰) = - cos 45⁰

1.За формулою = 1*2 + (-2)*(-4) + 3*3 = 2+8+9 = 19

2. Самостійно (д.з)

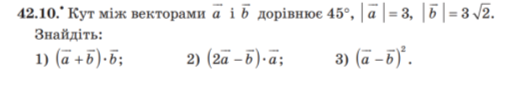
1)(=

2) самостійно (д.з)

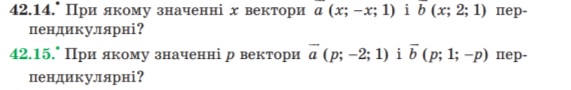
42.14. Вектори перпендикулярні якщо їх скалярний добуток = 0, отже

Підставляємо: х*х+2*(-х)+1*1 = 0

х²-2х+1=0

х₁*х₂ = 1                   

х₁+х₂ = 2

х₁ = 1; х₂= 2

Перевірка 1*1 -2*1 +1 =0 +

2*2-2*2 +1

В-дь: х = 1.

№ 42.15 – самостійно (д.з)