конспект уроку алгебри у 8 класі "Квадратні рівняння. Неповні квадратні рівняння та їх розв'язування."

8 клас

Алгебра

 

Тема уроку: Квадратні рівняння. Неповні квадратні рівняння та їх розв'язування.

Мета уроку: домогтися свідомого розуміння учнями означення квадратного рівняння, зведеного квадратного рівняння, неповного квадратного рівняння, назви коефіцієнтів квадратного рівняння: сформувати первинні вміння формулювати означення квадратного рівняння та його видів (зведеного та неповного), визначати коефіцієнти квадратного рівняння та за ними визначати вид квадратного рівняння; підготувати учнів до сприйняття наступного матеріалу (розв'язування неповних квадратних рівнянь); розвивати   вміння   вільно   висловлюватися  з теми,   відпрацьовувати   вміння  говорити коротко,    але   по   суті й переконливо: виховна: виховувати   активність, увагу,   інтерес   до нових знань і прагнення   їх   набути.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Квадратні рівняння», презентація, ноутбук, опорна схема, таблиця.

Хід уроку

І. Організаційний етап. Формулювання мети і завдань уроку. 

Добрий день.

Запишіть сьогоднішню дату та тему уроку. Сьогодні ми розпочинаємо вивчення нового розділу підручника «Квадратні рівняння»,  ознайомимося з різними  видами цих рівнянь, навчимося розв’язувати неповні квадратні рівняння, але перш ніж ми перейдемо до їх вивчення, давайте згадаємо, що ми знаємо про рівняння.

ІІ. Актуалізація опорних знань та вмінь.

1. Закінчіть речення:

1. Рівність, яка містить невідомі числа, позначені буквами – це … рівняння.
2. Число, яке при підстановці в рівняння дає істинну рівність  - це … корінь або розв’язок рівняння.
3. Розв’язати рівняння – це означає…  знайти всі його розв’язки (корені) або довести, що їх не існує.
4.  Рівняння, що мають ті самі корені (розв’язки) називаються…  рівносильними. Рівняння, які не мають коренів …  також рівносильні.
5. Рівняння виду ах=в, де а і в – довільні числа, а х – змінна,  … називається лінійним.
6. Лінійне рівняння може мати…

один корінь або безліч коренів або не  мати жодного кореня.

7. Корінь рівняння – це…

число, яке при підстановці в рівняння дає істинну рівність.

 

2. Усний рахунок

Чи є рівносильними рівняння?

а) 4х – 2 = х + 4                           і      3х – 6 = 0;

б) 5х – 1 = 3х – х2                        і      х2 + 2х – 1 = 0;

в) 5х2 – 10х + 25 = 0                   і      х2 – 2х + 5 = 0.

      2) Розв’яжіть рівняння.

а) у – 8 = 0 ;               б) х + 0,3 = 0 ;                в) 7х = 0 ;

 г) 2х -  4= 0;                 д) у +   = 0 ;               е) х ( х – 3 ) = 0

3. Математичний диктант. (Взаємоперевірка)

ІІІ. Засвоєння знань

План вивчення нового матеріалу

1. Мотивація навчальної діяльності.
2. Історична довідка.
3. Означення квадратного рівняння. Коефіцієнти квадратного рівняння.
4. Зведене квадратне рівняння.
5. Неповне квадратне рівняння. Види неповних квадратних рівнянь.

1. Мотивація навчальної діяльності

Завдання : розв’язати задачу -   Площа ділянки прямокутної форми дорівнює 600 м². Довжина ділянки на 10 м  більша від ширини. Знайти ширину ділянки.

(Для розв’язку задачі учні складають рівняння  х(х+10)=600, тобто х² +10х - 600=0  і не можуть його розв’язати)

- Одержане рівняння називається квадратним, і на наступному уроці ми навчимося розв’язувати такі рівняння.

2. Історична довідка: Розв’язувати квадратні рівняння вміли ще у Стародавньому Вавилоні  4 тис. років тому. Згодом розв’язували їх також у Китаї та Греції. Займались вивченням квадратних рівнянь такі видатні математики як Евклід і Діофант, Омар Хайям і Франсуа Вієт, Рене Декарт і Нільс Абель.

              Особливу увагу квадратним рівнянням приділяв Мухаммед аль-Хорезмі (ІХ ст.). Він показав, як знаходити додатні корені рівнянь.

             Індійські вчені у вирішені цього питання пішли далі. Математик Бхаскара (1114-1178), розв’язуючи рівняння знаходив і відֹ’ємні корені, зауважуючи при цьому, що їх « не слід брати, бо люди не схвалюють від’ємних абстрактних чисел».

             Французького математика Франсуа Вієта називають «батьком» алгебри. Він першим почав у рівняннях позначати буквами не тільки змінні, а й коефіцієнти, що дало можливість узагальнити способи розв’язування рівнянь.

3,   З деякими квадратними рівняннями ви теж вже зустрічались і можете їх розв’язати:  х² = 0,   х² – 4 = 0,   х² + 3х = 0,   та   х² – 4х + 4 = 0.

Усі вони мають вигляд   ах² + вх + с = 0.

Означення: Рівняння виду   ах² + вх + с = 0, де х – змінна,  а, в, с – числа, причому  а ≠ 0   називається квадратним.

       Назва такого рівняння походить від відповідного степеня  многочлена лівої частини рівняння.

       Число  а  називають першим або старшим коефіцієнтом, в – другим коефіцієнтом, с – вільним членом.

 Наприклад: Рівняння  2х² + 3х – 7 = 0  має такі коефіцієнти: а=2,  в=3, с= -7.

За дошкою таблиця, яку треба заповнити.

Рівняння	а	в	с
5х2+5х - 3=0
3х2+2х - 4=0
х2+4х + 3=0
-2х2 + х - 1=0
4х 2- 16х +4=0

 

3. Квадратне рівняння, перший коефіцієнт якого дорівнює 1, називається зведеним.

Наприклад:  останнє рівняння 4х²-16х+4=0 можна зробити зведеним, розділивши всі коефіцієнти на спільний дільник 4, отримаємо х ²- 4х +1=0.

          Квадратне рівняння, в якому, хоча б один із коефіцієнтів в або с дорівнює нулю, називають неповним квадратним рівнянням.

    

           Існують три види неповних квадратних рівнянь.

1. при    в = с = 0  маємо:   ах² = 0;
2. при    с = 0   і   в ≠ 0    маємо:    ах² + вх = 0;
3. при    в =0    і   с ≠ 0    маємо:     ах² + с = 0.

Розв’яжемо неповне рівняння кожного виду.

1. Рівняння    ах² = 0

                    х = 0        - єдиний корінь;

2. Рівняння     ах² + вх = 0

                     х ( ах + в ) = 0

                     х = 0   або   ах + в = 0

                                          ах = - в

                                          х = -             - два корені;

3. Рівняння    ах² + с = 0

                   ах² = - с

                   х² = -

при        х = √ -      або   х = - √ -        - два корені;    

при         - коренів немає.

Результати підсумовує така таблиця.

Класифікація видів квадратного рівняння

Назва рівняння	Числові коефіцієнти			Загальний вигляд рівняння	Схема розв’язку рівняння
	а	в	с
Повне				ах2+вх+с =0	D=b2- 4ac, якщо D>0, то х1,2 ; якщо D=0, то  х = - b/2а;  якщо D<0, то коренів немає.
Зведене	1			х2 + рх+q =0	х1 +х2 = - р;           х1 х2  =  q,
Неповне		0	0	ах2 =0	х2 =0; х = 0 – один корінь.
		0		ах2+с =0	ax2= - c; x2= - , якщо - с/а >0,  то х1= √ - с/а, х2 = - √  - с/а, два корені; якщо - с/а<0,  то коренів немає
			0	ах2+вх =0	х(ах +в) =0;  х1 = 0,    х2 =  - b/а

 

*Хвилинка релаксації

«Цифри»

Хід вправи: стоячи, за інструкціями вчителя виконуємо вправу: «Зараз ми будемо писати цифри у незвичний спосіб.

Цифру 1 «пишемо» носом (кажемо і виконуємо),

цифру 2 – підборіддям,

цифру 3 – правим плечем,

цифру 4 – лівим плечем,

цифру 5 – «пишемо» правим ліктем,

цифру 6  – лівим ліктем,

цифру 7  –  правим коліном,

цифру 8  –  лівим коліном,

цифру 9  – правою ногою,

а десяточку – «хвостиком».

IV. Розв’язування завдань, формування вмінь та навичок 

а) Усні вправи

1. Які з рівнянь є квадратними:

1) 5х² – 8 = 0;            2)  х² – х + 4 = 0;           3)   0,8х = 0;

4)   х² – 7 = 0;         5)   6х³ – 3х = 0;              6)   5х² = 0.

Для квадратних рівнянь знайдіть значення їх коефіцієнтів.

Виберіть серед них:

1) зведені;

2)  неповні квадратні.

2. Складіть квадратне рівняння,  у якому:

1)  Старший коефіцієнт дорівнює 6, другий коефіцієнт дорівнює   7, вільний член дорівнює  - 2.

2)  а =1     в = -  2      с = 3,5.

*Фізкультхвилинка                                           

Руки вгору підніміть,

Пряму лінію зобразіть, 

Потягніться і замріть,

Через боки опустіть.

Спинки ми тримаємо рівно,

І малюємо очима,

трикутник вершиною догори,

  а тепер вершиною донизу.

А тепер ми цифру вісім намалюєм вертикально,

 а тепер покладемо ми її горизонтально,

 в її центрі зупинись,

 зажмур очі – не лінись,

І по колу ти пройдись.

А тепер очі відкрили,

Поблимали,  закінчили.

 

 

V. Самостійна робота. (Самоперевірка)

1. Розв’язати рівняння :  1)                 2)

                                          3)          4)

VI. Повторення.   

VIІ. Підведення підсумків уроку.

• Яке рівняння називається квадратним?
• Чому а ≠ 0 ?
• Як називаються числа а, в, с?
• Скільки видів неповних квадратних рівнянь ви знаєте?
• Які рівняння ми називаємо зведеними?

 

 

VIІІ. Домашнє завдання

1. Вивчити зміст теоретичного матеріалу уроку. §20 Істер

2. Розв'язати вправи на закріплення вивченого матеріалу (аналогічних за змістом до вправ класної роботи). №781, 785, 796

3. На повторення: №804, 805

 

 

Додаткові матеріали до уроку

Класифікація видів квадратного рівняння

Назва рівняння	Числові коефіцієнти			Загальний вигляд рівняння	Схема розв’язку рівняння
	а	в	с
Повне				ах2+вх+с =0	D=b2- 4ac, якщо D>0, то х1,2 ; якщо D=0, то  х = - b/2а;  якщо D<0, то коренів немає.
Зведене	1			х2 + рх+q =0	х1 +х2 = - р;           х1 х2  =  q,
Неповне		0		ах2+с =0	ax2= - c; x2= - , х1= √ - с/а, х2 = - √  - с/а, якщо - с/а<0,  то коренів немає
			0	ах2+вх =0	х1 = 0,    х2 =  - b/а
		0	0	ах2 =0	х = 0

 

 

 

 

Опорна схема            Існують три види неповних квадратних рівнянь. при    в = с = 0  маємо:   ах2 = 0; при    с = 0   і   в ≠ 0    маємо:    ах2 + вх = 0; при    в =0    і   с ≠ 0    маємо:     ах2 + с = 0. Розв’яжемо неповне рівняння кожного виду. Рівняння    ах2 = 0                    х = 0        - єдиний корінь; Рівняння     ах2 + вх = 0                      х ( ах + в ) = 0                      х = 0   або   ах + в = 0                                           ах = - в                                           х = -             - два корені; Рівняння    ах2 + с = 0                    ах2 = - с                    х2 = - при     х = √ -    або   х = - √ -      - два корені;     при   < 0     - коренів немає.

 

 

 

 

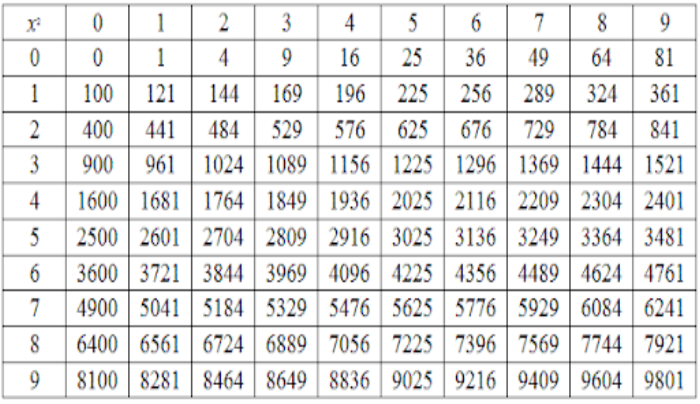
Таблиця квадратів до 99