Конспект уроку алгебри з теми "Числова функція. Способи задання функції"

КОНСПЕКТ УРОКУ АЛГЕБРИ

З ТЕМИ «ЧИСЛОВА ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ ФУНКЦІЇ»

10 клас, підручник: Математика (алгебра і початки аналізу та геометрія), Істер О.С.

Виконала: учитель Миколаївської ЗОШ

Босак Людмила Михайлівна

Тема уроку: «ЧИСЛОВА ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ

ФУНКЦІЇ»

Мета:  

1)      Освітня - узагальнення і систематизація знань і вмінь учнів про числові функції (означення, область визначення і область значень функції, способі задання); формування умінь знаходити область визначення і область значень функції, які задані аналітично.

2)      Розвиваюча - сприяти розвитку мислення й мови, уваги, формуванню умінь перенесення знань у нову ситуацію.

3)      Виховна - сприяти вихованню інтересу до математики, активності, мобільності, вміння спілкуватися, загальної культури.

Форми організації уроку: індивідуальна, групова.

Обладнання: дошка, крейда, указка, інтерактивна дошка, проектор, комп'ютер, картки із завданнями, фломастери, альбомні листи з системою координат.

Очікувані результати: учні повинні формулювати означення числової функції; знаходити значення функцій при заданих значеннях аргументу і значення аргументу, за яких функція набуває даного значення; користуватися різними способами задання функцій; знаходити область визначення і область значень функції, які задані аналітично.

Основні поняття: аргумент (незалежна змінна), функція (залежна змінна), значення функції  у точці , графік функції область визначення і множина значень функції, найбільше та найменше значення функції.

Компетентності, що формуються: математична – уміння оперувати числовою інформацією, знаходити значення функцій при заданих значеннях аргументу і значення аргументу, за яких функція набуває даного значення; користуватися різними способами задання функцій; установлювати за графіком функції її властивості; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; уміння вчитися впродовж життя.

Тип уроку: засвоєння нових знань і умінь.

Хід уроку

I.                Організаційний етап

II.            Мотивація та актуалізація навчальної діяльності

Процеси реального світу тісно пов'язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв'язок величин настільки тісний, що, знаючи значення однієї з них, можна визначити значення другої величини.

Наприклад, знаючи сторону квадрата, можна знайти його площу або периметр.

Залежність змінної у від змінної х, при якій кожному значенню x відповідає єдине значення у, називається функцією.

З поняттям функції ви познайомилися в курсі алгебри. Поняття функції є важливим поняттям курсу алгебри і початків аналізу, отже, ми повинні згадати і узагальнити відомості про функції. Крім того, досліджуючи властивості функцій, ми має­мо можливості ґрунтовніше пізнати реальний світ.

Парабола в природі

Парабола в архітектурі

III.    Сприймання та усвідомлення нового матеріалу

План вивчення матеріалу

1. Поняття функції, її області визначення і множини значень.

З функцією ми почали знайомитися в курсі алгебри основної школи.

Нагадаємо означення функції.

Числовою функцією (або функціональною залежністю) називають таку залежність між двома змінними, при якій кожному значенню незалежної змінної з деякої множини відповідає за певним правилом єдине значення залежної змінної.

Нагадаємо, що функції, зазвичай, позначають латинськи ми (інколи грецькими) літерами.

Розглянемо функцію f, у якої кожному натуральному значенню х від 1 до 5 відповідає число y, удвічі більше за x (мал. 1.1). Стрілка вказує на число y, яке відповідає числу х. Число у називають значенням функції f у точці х і позначають через f(x). На малюнку 1.1, зокрема, f(3) = 6.

Нагадаємо, що незалежну змінну x

ще  називають аргументом функції, а про залежну змінну у кажуть, що вона є функцією від цього аргументу.

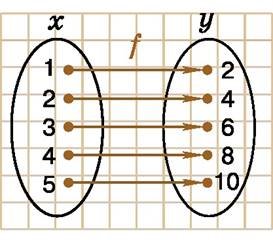
Мал. 1.1

Областю визначення функції y = f(x) називають множину всіх значень, яких може набувати аргумент х.

Позначають область визначення символом D(f) або D(y). Наприклад, областю визначення функції, яку ми розглянули вище, є множина, що складається із чисел 1, 2, 3, 4, 5, тобто D(f) = {1; 2; 3; 4; 5}, а областю визначення функції у = х² - 2х + 3 є множина всіх дійсних чисел, що можна записати так: D(y) = R.

Задача 1. Знайти область визначення функції:

1)           ; 2) .

Розв'язання. 1) Оскільки знаменник дробу не може дорівнювати нулю, то областю визначення функції є множина усіх значень х, для яких х +1≠0, тобто х ≠ -1. Отже, D(y) = (-∞;-1) U (-1; +∞).

2)           Оскільки підкореневий вираз має бути невід'ємним, то областю визначення функції є множина всіх тих значень х, для яких х – 2 ≥ 0, тобто х ≥ 2. Отже, D(y) = [2; +∞). Відповідь. 1) D(y) = (-∞; -1) U (-1; +∞); 2) D(y) = [2; +∞).

Множиною (або областю) значень функції y = f(x) називають множину, що складається з усіх чисел f(x), де х є D(f).

Позначають множину значень символом E(f) або E(y). Для функції на малюнку 1.1 маємо: E(f) = {2; 4; 6; 8; 10}. Щоб знайти множину значень функції у = х² - 2х + 3, перетворимо вираз, який записано у формулі функції:

x² - 2х + 3 = х² - 2х + 1 + 2 = (х - 1)² + 2.

Отже, функцію можна записати у вигляді: у = (х - 1)² + 2. Оскільки  (х-1)² ≥ 0, то (х - 1)² + 2 ≥ 2. Тому E(y) = [2; +∞).

Задача 2.

Знайти область значень функції у = 3 - √х. Розв'язання. За означенням арифметичного квадратного кореня: √х ≥ 0. Тоді: -√х ≤ 0. Далі додамо до обох частин цієї нерівності число 3, отримаємо: 3 - √х ≤ 3, тобто у ≤ 3. Тому E(y) = (-∞; 3].

Відповідь. E(y) = (-∞; 3].

Як відомо, функції є математичними моделями реальних процесів і явищ навколишнього світу. Тому їх часто застосовують під час дослідження різноманітних проблем у фізиці, економіці, біології тощо.

Задача 3.

Записати формулу для обчислення кінетичної енергії кульки масою 50 г. З'ясувати, чи задає ця формула функцію, i, якщо так, вказати ii аргумент.

Розв'язання. Як відомо, кінетичну енергію  обчислюють за

формулою . Тому маємо: , тобто  

Відповідь:  є функцією від аргументу v, де v ≥ 0.

2. Способи задання функцій

Нагадаємо, що функцію можна задавати різними способами:

формулою, графіком, таблицею, словесно тощо.

Наприклад, кожну з функцій, які ми розглянули вище,

P(t) = 200 000 * 0,95

t, задано формулою. Цей спосіб задання функції є

досить зручним, адже дає змогу для довільного значення аргументу з області визначення функції знайти відповідне йому значення функції, а часто розв'язати й обернену задачу.

Словесний спосіб задання функції полягає в тому, що функціональну залежність формулюють словами. Наприклад, «кожному числу x ставимо у відповідність квадрат цього числа, зменшений на 10». Якщо сказане задати формулою, то вона виглядатиме так: y = x² - 10.

Словесний спосіб задання функції використовують дуже рідко.

Задача 4.

Функцію задано формулою

1)      Знайти значення функції для x = 4.

2)      Порівняти y(0) і y(1).

3)      Знайти, при якому значенні аргументу значення функції дорівнює 0.

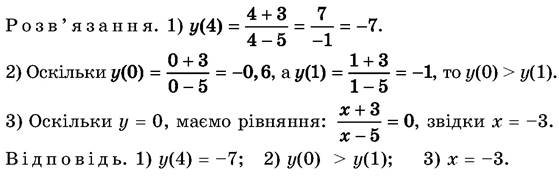
3. Графік функції

Графіком функції називають множину всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним їм значенням функції.

Раніше ми вже працювали з функціями вигляду y = kx + b,

у = x, у = ax² + bx + c. Використовуючи довідкову

літературу та комп'ютерні програми для побудови графіків функцій, пригадайте властивості цих функцій та вигляд їх графіків.

Побудуємо графіки деяких функцій за допомогою комп’ютерної програми GeoGebra (мал 1.2, мал 1.3).

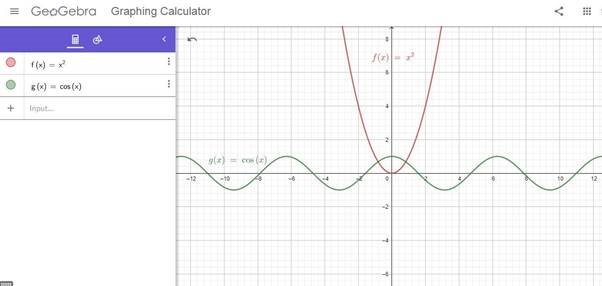
Мал. 1.2. Вигляд середи побудови графіків GeoGebra

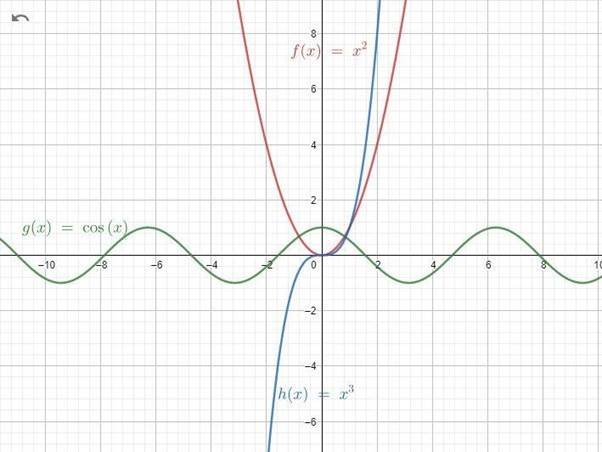
Мал. 1.3. Графіки функцій, побудованих в програмі GeoGebra IV.          Осмислення нового матеріалу.

1) Відповісти на питання:

-         Що називають числовою функцією? 

-         Що називають областю визначення функції і що множиною значень функції? 

-         Назвіть способи задання функцій, до кожного наведіть приклади. Що називають графіком функції? 

-         Пригадайте, як будувати графіки за допомогою перетворень графіків функцій.

2) Виконання вправ.

Вправа 1.

Початкова вартість деякого обладнання складає 200 000 грн. Щороку вона зменшується на 5 %. Знайти:

1)                функцію P залежності вартості обладнання від терміну експлуатації t (років);

2)                використовуючи функцію P, вартість обладнання через 4 роки. Розв'язання. 1) За умовою щороку вартість обладнання становитиме 100 % - 5 % = 95 % від вартості обладнання за минулий рік. Тому вартість обладнання складатиме:

через рік - 200 000 * 0,95,

через 2 роки – 200 000 * 0,95 * 0,95 = 200 000 * 0,95², ...,

t через t років - 200 000 * 0,95 .

Маємо функцію:

t

P(t) = 200 000 * 0,95 , де t є N.

2) Якщо t = 4, то P(4) = 200 000 * 0,95⁴ = 16 2 901,25 (грн). 

Відповідь. 

t

1)               P(t) = 200 000 * 0,95 ; 2) 162 901,25 грн.

Вправа 2.

Формула описує зміну температури води в баку (у °С) залежно від часу t (у хв):

                 Знайти: 1) p(10); 2) p(45);      3) p(80).

Розв'язання. 1) Оскільки 0 < 10 < 40, то p(10) обчислюємо за формулою p(t) = 2t + 20. Отже, p(10) = 2 * 10 + 20 = 40.

2)               Оскільки 40 < 45 < 50, то p(45) = 100.

3)               Оскільки 50 < 80 < 120, то p(80) обчислюємо за формулою р =  0,8t + 140. Отже, р(80) = -0,8 * 80 +140 = 76. 

Відповідь. 1) 40; 2) 100; 3) 76.

Функцію також можна задавати таблицею. Табличний спосіб задання дозволяє безпосередньо вказати значення функції, але лише для скінченного набору значень аргументу.

Припустимо, щогодини, починаючи з дев'ятої ранку і до п'ятнадцятої, вимірювали атмосферний тиск і результат заносили в таблицю:

У результаті отримали функцію, область визначення якої складається із чисел 9; 10; 11; 12; 13; 14; 15 (числа першого рядка таблиці), а множина значень - із чисел 753; 754; 755; 757 (числа другого рядка таблиці).

Часто функцію задають за допомогою графіка. Графічний спосіб задання дає можливість унаочнити властивості функції.

На малюнку 1.4 зображено вольт-амперні характеристики деяких електричних елементів, тобто залежність сили струму від напруги задано графічно. Цю залежність отримано не за допомогою формули, а експериментальним шляхом.

На малюнку 1.5 зображено кардіограму людини. Кардіограму можна вважати графіком зміни електричного потенціалу на волокнах серцевого м'яза під час його скорочень.

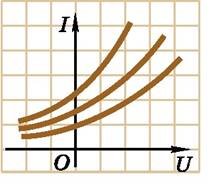
Мал. 1.4.

Мал. 1.5.

Вправа 3.

За графіком функції y = f(x) на малюнку 1.6 знайти: 1) область визначення функції; 2) множину значень функції; 3) значення функції для x = -1; x = 2; 4) значення аргументу, при яких у = -1; у = 3.

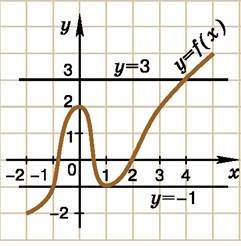
Мал. 1.6.

Розв'язання. 1) Спроектуємо всі точки графіка на вісь x. Отримаємо проміжок [-2; 5]. Отже, D(y) = [-2; 5].

2)      Спроектуємо всі точки графіка на вісь y. Отримаємо проміжок

[-2; 4].

Отже, E(y) = [-2; 4].

3)      За графіком: y(-1) = -1; y(2) = 0.

4)      Оскільки пряма y = -1 перетинає графік у точках з абсцисами x = -1 і x = 1, то f(x) = -1 для x = -1 або x = 1. Пряма y = 3 перетинає графік у точці з абсцисою 4. Отже, f(x) = 3, якщо x = 4.

Відповідь. 1) D(y) = [-2; 5]; 2) E(y) = [-2; 4]; 3) у(-1) = -1; y(2) = 0; 3) f(x) = -1, якщо x = -1 або x = 1; f(x) = 3, якщо x = 4.

Виконання тестових завдань.

Варіант 1

1.     Обчислити значення функції  f (х) = ⁵   в точці   х₀ = ¹ х        5

          а) 25 ;                                                б) 1 ;

          в) 0 ;                                                г) інша відповідь.

2.     Знайти область визначення функції у = ⁸

х8

           а) [8; +_);                                         б) (-_;8);

           в) (8; +_);                                        г) інша відповідь.

3.     Знайти координати точок перетину графіків функцій        у = х+2 ,  у = ⁸  не виконуючи побудови х

          а) (2; 4) ;                                           б) (-4; -2) ;

          в) (2; 4) ; (-4;-2);                              г) інша відповідь.

4.     Знайдіть область визначення функції  у =   ^х2      + х6 208хх²

Варіант 2

1.   Обчислити значення функції  f (х) = ⁶   в точці   х₀ = ¹ х    6

          а) 36 ;                                                б) 1 ;

          в) 0 ;                                                г) інша відповідь.

2.   Знайти область визначення функції у = х9

           а) (-9; +_);                                        б) (-9; 9);

          в) [-9; +_);                                      г) інша відповідь.

3.   Знайти координати точок перетину графіків функцій  у = х+3, у = ⁴ не виконуючи побудови

х

          а) (0; 3),  (-3; 0);                                б) (-4; 3) ;

          в) (1; 4) ; (-4; -1)                              г) інша відповідь.

4.   Знайдіть область визначення функції  у =          ^х1       х1 103хх²

Відповіді до тесту

V.            Підбиття підсумків уроку

VI.         Домашнє завдання 1) Опрацювати параграф 1.

2) Виконати вправи: