Конспект уроку "Частота та ймовірність випадкової події". Алгебра, 9 клас
|
|
Алгебра |
|||||
|
Урок |
Урок № 52 |
Урок № 51 |
Урок № 75 |
Урок № 75 |
Урок № 75 |
|
|
Клас |
9-А |
9-Б |
9-В |
9-Г |
9-Д |
|
|
Дата проведення уроку |
09.04.2019 |
08.04.2019 |
05.04.2019 |
05.04.2019 |
05.04.2019 |
|
|
Тема уроку |
Частота та ймовірність випадкової події |
|||||
|
Мета уроку |
Формування предметних компетентностей:
Формування ключових компетентностей:
|
|||||
|
Тип уроку |
Засвоєння нових знань і вмінь учнів |
|||||
|
Форма проведення |
Фронтальна бесіда, практичний метод розв’язування завдань, колективна та індивідуальна робота |
|||||
|
Наочність та обладнання |
опорний конспект, збірник завдань для ДПА, презентація |
|||||
|
Перебіг уроку |
||||||
|
№ з/п |
Етапи уроку |
Методи та прийоми. На що звернути увагу |
||||
|
І |
Організаційний |
Перевірити готовність учнів до уроку та налаштувати їх на роботу |
||||
|
ІІ |
Перевірка домашнього завдання
|
Перевірити наявність та якість виконання домашнього завдання та відповісти на запитання учнів, які виникли під час виконання завдань. В індивідуальному порядку перевірити роботи учнів, які потребують додаткової педагогічної уваги. |
||||
|
ІІІ |
Мотивація нав-чальної діяль-ності |
Нам часто доводиться проводити різні спостереження, досліди, брати участь у експериментах або випробуваннях. Часто такі експерименти завершуються результатами, які заздалегідь передбачити неможливо. Наприклад, ми купуємо лотерейний квиток і не знаємо, виграємо чи ні. Чи можна якимось чином оцінити шанс появи результату, який нас цікавить? Відповідь на це питання дає розділ математики, що називається теорія ймовірностей. Доповнення знань учнів про способи обчислення ймовірності випадкової події
|
||||
|
ІV |
Формулювання мети й завдан- ня уроку |
Основна мета - ознайомити учнів з областю задач комбінаторики; сформувати вміння знаходити ймовірність випадкової події |
||||
|
V |
Актуалізація опорних знань учнів |
Розв’яжи задачу: 1. У коробці лежать 5 червоних та 7 зелених олівців. Скільки існує способів вибору з коробки одного зеленого або одного червоного олівця? (12 способів) 2. У їдальні пропонують чотири види тістечок та три види напоїв: молоко, компот, чай. Скільки існує способів вибору сніданку, що складається з одного тістечка та одного виду напоїв? (12 способів) Які правила використовували при розв’язуванні цих задач? |
||||
|
VІ |
Вивчення нового матеріалу:
|
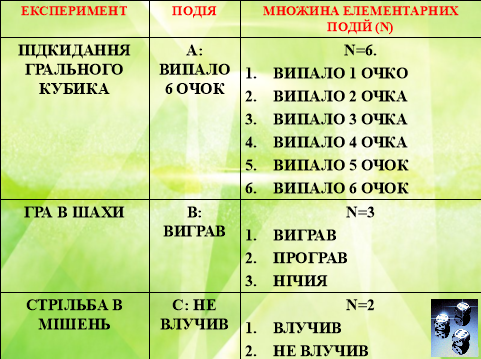
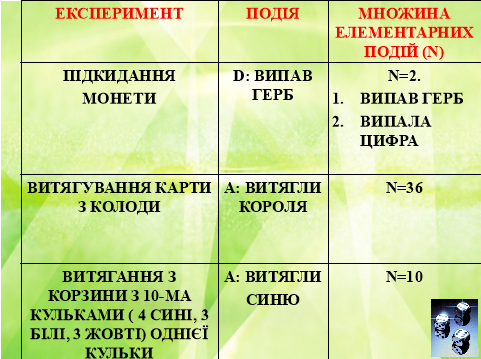
І. Основні поняття теорії ймовірностей: 1. Експеримент 2. Випадкова подія
Властивості елементарних подій:
|
||||
|
VІІ |
Удосконалення знань та вмінь учнів |
Виконати письмово:
ІІ. Класичне означення ймовірності
А – випадкова подія Р(А) – ймовірність випадкової події m – кількість сприятливих подій n – загальна кількість подій
Якщо подія А вірогідна, то Р(А) = 1. Якщо подія А неможлива, то Р(А) = 0. Якщо подія А випадкова, то 0 < Р(А) < 1.
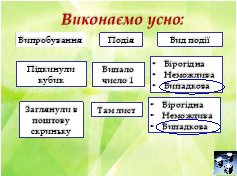
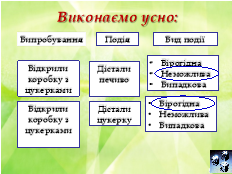
Виконаємо усно: 1. Знайти ймовірність того, що під час підкидання грального кубика випаде 9 очок Р(А) = 0 2. Знайти ймовірність того, що під час підкидання грального кубика випаде менше ніж 7 очок Р(А) = 1 3. Знайти ймовірність того, що під час нагрівання вода перетвориться на лід Р(А) = 0 4. Знайти ймовірність того, що після ночі настане день Р(А) = 1 Виконаємо письмово (парна робота): № 1. Яка ймовірність того, що при одному киданні грального кубика випаде число очок, що дорівнює:
2) П'яти; 3) Парному числу; 4) Числу, яке кратне 6?
Відповідь:
1) № 2. У гральній колоді 36 карт. Навмання вибирається одна карта. Яка ймовірність того, що ця карта:
2) Бубновий туз?
Відповідь:
1)
№ 3. В ящику знаходиться 45 кульок, з яких 17 білих. Загубили дві не білих кульки. Яка ймовірність того, що вибрана навмання одна кулька буде білою?
№ 5. У коробці 4 сині, 3 білі та 2 жовті кульки. Яка ймовірність того, що витягнута навмання кулька: а) біла; б) жовта; в) синя?
№ 6. Одночасно кидають два кубика. Яка ймовірність того, що сума очок, які випали на обох з них, дорівнює восьми?
№ 7. Із слова ІСПИТ випадково обирають одну букву. Яка ймовірність того, що вона буде: а) голосною; б) приголосною ? Відповідь:
№ 8. Знайти ймовірність випадання більше чотирьох очок при підкиданні грального кубика
Перевір себе (індивідуальна робота учнів): 1. Яка ймовірність того, що при падінні грального кубика випаде 5 очок? 2. Яка ймовірність того, що під час підкидання монети випаде герб? 3. Яка ймовірність того, що назване навмання трицифрове число виявиться меншим за 1000? 4. В коробці є 3 блакитних і 8 жовтих куль. Яка ймовірність того, що витягнута кулька блакитна ? 5. Яка ймовірність того, що витягнута навмання карта з колоди виявиться королем? Відповідь:
1) ; 2) ; 3) 1 ; 4) ; 5)
|
||||
|
VІІІ |
Робота з учня-ми, що мають почат-ковий рівень навч. досягнень |
Індивідуальні консультації
|
||||
|
ІХ |
Підсумки уроку |
|
||||
|
Х |
Рефлексія |
Кожен учень у зошиті ставить один із знаків |
||||
|
ХІ |
Домашнє завдання |
Вивчити: п. 22 Виконати: № 22.4, № 22.10, № 22.15, № 23.13, № 23.16, № 23.18, № 23.23 Повторити: п.18 |
||||
|
ХІІ |
Підготовка до ДПА |
В – 66, В – 67 ДПА |
||||
Домашнє завдання:
Відповіді:
№ 22.10
![]()
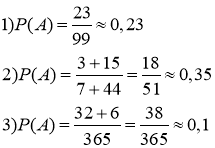 № 22.15
№ 22.15
№ 23.13
![]()
№ 23.16
![]()
№ 23.18
![]()
№ 23.23
Нехай у коробці х червоних кульок, тоді усього у коробці (4 + х) кульок.
![]() Подія А: вибрана кулька – синя.
Подія А: вибрана кулька – синя.
За умовою
Маємо рівняння:
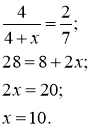
Відповідь: 10 червоних кульок.


про публікацію авторської розробки
Додати розробку





-

Дуборез Альона Василівна
12.10.2021 в 18:46
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Голубек Олена Анатоліївна
14.04.2021 в 20:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
05.04.2021 в 12:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рамазанова Ганна Олексвївна
02.03.2021 в 23:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сема Наталя
06.04.2020 в 19:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука