Конспект уроку " Додавання та віднімання раціональних чисел" у 6 класі

 

 

 

 

по темі:

 

 

 

 

 

 

 

 

 

 

 

Очікувані результати

Після цього уроку учні зможуть:

• Додавати і віднімати раціональні числа;
• Аналізувати свою роботу та роботу своїх товаришів;
• Застосовувати набуті знання при розв’язуванні різноманітних задач в подальшому.
• Логічно мислити над математичними задачами та вправами;
• Нетрадиційно підходити до розв’язування деяких математичних задач.

 

Орієнтовний план і методи проведення уроку:

1. Організаційний етап.
2. Мотивація навчальної діяльності.
3. Повідомлення теми, мети уроку.
4. Актуалізація опорних знань.
5. Розв’язування вправ:

•     додавання двох від’ємних чисел;
•     додавання двох чисел з різними знаками;
•     віднімання чисел з різними знаками.

6. Підсумки уроку.
7. Домашнє завдання.

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА:Додавання та віднімання раціональних чисел.

 

МЕТА:

освітня:систематизувати знання учнів про раціональні числа, модуль числа додавання і віднімання раціональних чисел;

розвиваюча:розвивати логічне мислення, культуру математичної мови і записів;

виховна: виховувати самостійність, інтерес до математики, взаємодовіру.

 

ТИП УРОКУ:узагальнення та систематизація знань, умінь та навичок.

 

НАОЧНІСТЬ ТА ОБЛАДНАННЯ:девіз уроку, табличка «ДОВІДКОВЕ БЮРО», сигнальні картки, картки самоконтролю, картки завдання; підручник для 6 класу: Математика, Бевз Г.П., Бевз В.Г.

 

ДЕВІЗ:Розум полягає не лише в знаннях,

але й у вмінні застосовувати ці знання.

Аристотель

 

 

 

 

 

 

 

 

 

 

 

 

 

І. Організаційний етап.

- Доброго ранку, друзі мої! Сьогодні гарний день, то ж посміхнімося і подаруймо чарівну посмішку один одному  і присутнім гостям на уроці.

Вона триває мить, а в пам’яті, часом, залишається назавжди. Від неї добре, тепло, стає гарним настрій. От з таким настроєм ми й будемо працювати упродовж усього уроку.

Девізом якого є слова відомого математика Аристотеля «Розум полягає не лише в знаннях, але й у вмінні застосовувати ці знання».

 

ІІ. Мотивація навчальної діяльності

Сьогодні на уроці ми узагальнимо та систематизуємо знання з теми «Додавання та віднімання раціональних чисел», повторимо правила порівняння, додавання та віднімання раціональних чисел, перевіримо, чи навчились ви розкривати дужки, закріпимо виконання відповідних дій та вдосконалимо їх.

 

ІІІ. Повідомлення теми, мети уроку.

А проведемо наш урок у вигляді історичної мандрівки  стрічкою часу.Здійснювати цю подорож ми будемо чарівним «Математичним експресом», який буде переносити нас у минуле, у часи виникнення раціональних чисел. А свою  роботу  на різних етапах  ви будете оцінювати у картці самоконтролю, яка лежить на ваших партах.

 Тож запишемо у зошити тему уроку «Додавання та віднімання раціональних чисел».

Тож до роботи. Давайте на практиці використовувати наш девіз і починати нашу подорож. СТАРТ!!!

 

 

ІV. Актуалізація опорних знань.

Інтерактивна вправа «Мікрофон»

На цьому етапі потрібно привести «М.Е» в повний порядок: перевірити роботу усіх частин поїзда, розкласти все по своїх місцях, щоб нічого не заважало в подорожі. Для цього потрібно дати відповіді на запитання. Кожен, хто відповідає, звичайно, якщо відповідь є правильною, у картці самоконтролю ставить собі знак «+».

1. Які числа називаються цілими?

(Натуральні числа, протилежні їм і число 0 разом називаються цілими числами)

2. Які числа називаються раціональними?

(Цілі і дробові числа разом називаються раціональними числами)

3. Додатне чи від’ємне число нуль?

(Число 0 – ні додатне, ні від’ємне)

4. Що таке модуль раціонального числа?

(Модулем раціонального числа називається це саме число,  якщо воно не від’ємне, або протилежне йому число, якщо воно від’ємне)

5. Як називаються компоненти дії додавання?

(Компоненти дії додавання називаються: доданок, доданок і сума)

6. Як додати два від’ємні числа?

(Щоб додати два від’ємні числа, треба додати їх модулі і перед результатом поставити знак мінус)

7. Як знайти суму додатного та від’ємного числа?

(Щоб додати додатне і від’ємне число, треба знайти різницю їх модулів і перед результатом поставити знак числа з більшим модулем)

8. Чому дорівнює сума двох протилежних чисел?

(Сума двох протилежних чисел дорівнює нулю)

9. Як називаються компоненти дії віднімання?

(компоненти дії віднімання називаються: зменшуване, від’ємник і різниця)

10.   Як від одного раціонального числа відняти друге?

(Щоб від одного числа відняти друге, треба до зменшуваного додати число, протилежне від’ємнику)

11.   Як розкрити дужки, перед якими стоїть знак плюс?

(Щоб розкрити дужки у виразі, перед яким стоїть знак «+», досить опустити дужки і знак перед ними)

12.   Як розкрити дужки, перед якими стоїть знак мінус?

(Щоб розкрити дужки у виразі, перед яким стоїть знак «-», досить опустити дужки і знак перед ними, а знаки доданків, які були в дужках, змінити на пролежні)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V століття до нашої ери

V. Розв’язування вправ.

Отже клас добре підготувався до уроку, всі повторили теоретичний матеріал, тож розпочнемо нашу мандрівку. А все почалося із V століття до нашої ери. А що означає ця дата? із цим питанням ми звернемось до ДОВІДКОВОГО БЮРО

ДОВІДКОВЕ БЮРО.На ранніх ступенях розвитку люди знали тільки натуральні числа, але з розвитком цивілізації перед людством постає питання: як відняти більше число від меншого? Назва раціональні числа походить від латинського слова ratio, яке означає відношення. Бо кожне раціональне число дорівнює відношенню деяких двох цілих чисел. Латинські слова plus i minus означають відповідно більше і менше.

V століття до нашої ери – це час появи від’ємних чисел. А саме – їх розглядами китайські математики. Додатні числа вони писали червоною фарбою, а від’ємні – чорною.  Однак від’ємними числами користувалися тільки деякі вчені.

Інтерактивна вправа «Мозковий штурм»

Робота в групах. Три групи отримують картки із завданнями: рівняння з модулями. Для пошуку розв’язання учні працюють у групах, висуваючи та обговорюючи різні ідеї.

1)

2)

3)

 

 

 

 

Нуль

ДОВІДКОВЕ БЮРО.Своєрідною координатною прямою є стрічка часу, на якій зображують роки і століття. Християни за початок відліку часу приймають день народження Ісуса Христа – Різдво Христове. Час після цього дня називають новою ерою, а до того – до нової ери. Ось цією стрічкою ми сьогодні і мандруємо.

Гра «Естафета»

Гравці команд по черзі розв’язують завдання, що записані на дошці.

А	12	-5	0	-2	-8	12
В	18	3	4	-1	-6	-10
А+В	30	-2	4	-3	-14	2
А-В	-6	-8	-4	-1	-2	22

А	6	-2	0	-6	9	3
В	15	-1	-5	-7	-9	-3
А+В	21	-3	-5	-13	0	0
А-В	-9	-1	5	1	18	6

 

А	13	-3	0	-5	9	5
В	8	-4	-6	7	-10	-5
А+В	21	-7	-6	2	-1	0
А-В	5	1	6	-12	19	10

 

 

 

 

 

 

 

 

VІІ століття нашої ери

ДОВІДКОВЕ БЮРО.VІІ ст. н. е. - поява від’ємних чисел в Індії, де їх пов’язували з боргом, а додатні – з майном. Правила дій над додатними і від’ємними числами формулювали так: «сума двох боргів є борг», «сума майна і боргу дорівнює їх різниці», «добуток двох боргів є майном».

Цікава задача-ілюстрація.

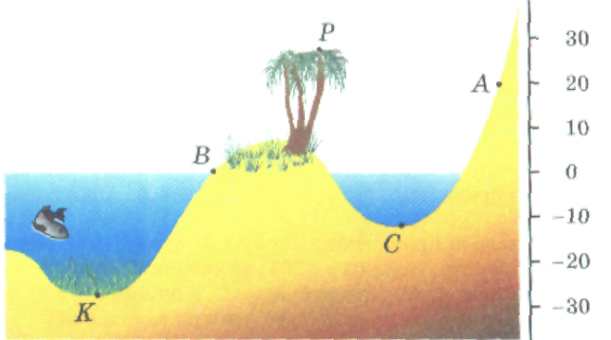
Визначте, як розташовані точки А, В, С, К і Р:

а) відносно рівня моря;

б) відносно одна одної.

 

 

 

 

 

 

 

 

 

 

 

ХV століття

ДОВІДКОВЕ БЮРО.ХV ст. - це час, коли від’ємні числа стали відомими у Європі. Користувались ними дуже рідко. Більшість європейських математиків називали їх «несправжніми», «вигаданими», «абсурдними», «хибними» числами. Тільки починаючи з XVІІ ст., коли вчені все частіше використовували координати точок, вони поступово звикли до від’ємних чисел. Тепер математика, фізика та інші науки не можуть обійтися без від’ємних чисел.

Тести з сигнальними картками

На дошці записано два числа -11 та 3. Учні відповідають на питання:

1. Чому дорівнює модуль першого числа?

А) 11                               Б) -11                              В) 0

     2. Яке з чисел більше?

А) -11Б) 3                              В) неможл. визн

3. Чому дорівнює сума цих двох чисел?

А) 8Б)-8                               В) -14

4. Чому дорівнює сума цих двох чисел?

А) -14                               Б) -8                              В) 8

5. Сума першого числа і числа, протилежного другому числу?

А) -8                               Б) 14В) -14

6. Які числа лежать на координатній прямі між даними?

А) -9, 4, -1Б) 0, -8, 1В) 16, -1, 0

7. Чи правильна рівність ?

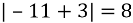А) так                               Б) ніВ) не знаю

8. Чи правильна рівність ?

А) такБ) ніВ) не знаю

 

 

 

ХVІ століття

ДОВІДКОВЕ БЮРО.  16 ст.Сучасні позначення додатних і від’ємних чисел із знаками «плюс» і «мінус» ввів німецький математик Відман. Однак ще і 16 столітті багато математиків не визнавали від’ємних чисел.

VІ. Підсумки уроку

- Опрацюйте картку самоконтролю і виставте собі оцінку

Картка самоконтролю
Прізвище, ім'я _______________________________________
Вид діяльності на уроці								найвищий бал		бал за роботу
"Мікрофон"								1
"Мозковий штурм"								3
Гра "Естафета"								1
Задача-ілюстрація								3
Тести з сигнальними картками
1	2	3	4	5	6	7	8	0,5
Всього балів								12

Учні працюють з відкритими реченнями, продовжуючи  їх:

«На сьогоднішньому уроці ми дізналися …»

«Найбільше мені сподобалось…»

«Найважливішим відкриттям для мене було …»

«Я тепер знаю…»

 

VІІ. Домашнє завдання

Впр. 1057, 1060, 1061, 1461- (для учасників конкурсу «Кенгуру»).