Конспект уроку на тему "Дії над векторами, що задані координатами. "
Урок № 40-41
Тема: Дії над векторами., що задані координатами. Формули для обчислення довжини вектора, кута між векторами, відстані між двома точками.
Мета: Узагальнити та систематизувати вміння студентів з теми:”Вектори і координати в просторі”. Реалізувати поняття скалярного добутку між векторами, довжини вектора, кута між векторами, що задані коордитнатами. Формувати вміння та навички студентів застосовувати вивчений матеріал до розв’язування задач.
Виховувати культуру мови в ході бесіди, математичну культуру, навики самостійно приймати рішення; створювати передумови формування загальнолюдських вмінь та навиків студентів, формувати творчий та естетичний потенціал студентів.
Тип уроку: Заняття узагальнення та систематизації знань, умінь, навичок.
Методи навчання:
- Проблемної бесіди
- Поясненнювально-ілюстративний
- Тренувальні вправи
Види діяльності:
- Самостійна робота
- Фронтальна робота
- Індивідуальна робота
Обладнання: комп’ютер, екран, проектор
Дидактичні матеріали: Варіанти завдань для тестового опитування, таблиця ”Вектори і координати в просторі”.
План уроку
1. Формула для обчислення довжини вектора. Приклади.
2. Скалярний добуток векторів. Приклади.
3. Кут між векторами, що задані своїми координатами. Умова ортогональності векторів. Приклади.
4. Тестове опитування.
Хід роботи
І. Організаційний момент
ІІ. Перевірка домашнього завдання.
ІІІ. Актуалізація знань.
Самостійна робота.
І рівень (2 бали)
1. Координати вектора ![]() , якщо
, якщо ![]() дорівнюють …
дорівнюють …
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Який вектор дорівнює сумі векторів ![]() і
і ![]() ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
ІІ рівень (4 бали)
3.Якщо А(-2;4;1), В(3;-7;1), то координати вектора ![]() …
…![]()
а) ![]() ; б)
; б)![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
4. Знайдіть довжину вектора ![]() ?
?
а)![]() ; б)
; б)![]() ; в)14; г)
; в)14; г)![]() ;
;
ІІІ рівень (6 балів)
5. Дано вектори ![]() і
і ![]() . Знайти абсолютну величину вектора
. Знайти абсолютну величину вектора ![]() .
.
ІV рівень (9 балів)
6.Знайти число х, якщо модуль вектора ![]() дорівнює 3,
дорівнює 3, ![]() (1;0;1),
(1;0;1), ![]() (1;2;0).
(1;2;0).
Відповідь: 1 б); 2 в); 3 в); 4 а); 5) ![]() ; 6) х1=1, х2=-2
; 6) х1=1, х2=-2
IV. Мотивація пізнавальної діяльності

Безпосереднє відношення до введення координатного методу в математиці має Рене Декарт. Математичні праці Декарта випливали з його філософських поглядів. Природою матерії, учив Декарт, є її тривимірювана об'ємність (довжина, ширина і висота), а найважливішою особливістю — ділимість і рухомість. Ці особливості і властивості матерії і повинна досліджувати математика. Тому математику як науку необхідно побудувати за єдиним аналітичним методом, який відображав би кількісні зміни вічно рухомої матерії.
Ці прогресивні наукові ідеї Декарт втілив у виданому в 1637 р. знаменитому творі «Міркування про метод». У ньому він показав, як аналітичний метод можна застосувати до дослідження деяких питань фізики і математики. У пізнішій своїй праці «Числення пана Декарта» учений докладніше показав, як його аналітичний метод можна застосувати, пов'язавши алгебру з геометрією.



V. Вивчення нового матеріалу
1. Формула для обчислення довжини вектора. Приклади.
На попередньому занятті ми з вами з’ясували, що довжиною вектора є довжина відповідного йому відрізка. Отже, якщо вектор визначено початком і кінцем в точках відповідно: ![]() і
і ![]() , то довжиною вектора буде величина, що дорівнює:
, то довжиною вектора буде величина, що дорівнює:
![]() (1)
(1)
Якщо ж координати вектора відомі: ![]() , то його довжина відповідно буде дорівнювати:
, то його довжина відповідно буде дорівнювати:
![]() . (2)
. (2)
Для закріплення нових формул пропоную наступні приклади:
№1. Дано точки ![]() і
і ![]() . Знайти довжину вектора
. Знайти довжину вектора ![]() .
.
Розв’язування.
За формулою (1): ![]() =
= ![]() =
=
=![]() .
.
№2. Знайти довжину вектора ![]() .
.
Розв’язування.
За формулою (2): ![]() =
=![]() =
=![]()
№3. Знайти довжину вектора ![]() , якщо
, якщо ![]() ;
; ![]() .
.
Розв’язування.
![]() , тоді
, тоді ![]()
№4. Знайдіть довжину діагоналі АС паралелограма ABCD, якщо А (2; - 6; 0), В (-4; 8; 2), D (0;-12;0).
Розв'язування
Оскільки ![]() (- 6; 14; 2),
(- 6; 14; 2), ![]() (-2; -6; 0), то
(-2; -6; 0), то ![]() =
= ![]() +
+ ![]() , AC (-8; 8; 2)
, AC (-8; 8; 2)
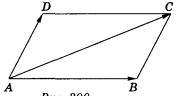 (рис. 300).
(рис. 300).
Тоді ![]() =
= ![]() =
= ![]() = 2
= 2![]() (лін. од. )
(лін. од. )
2. Скалярний добуток векторів. Приклади.
Скалярним добутком векторів ![]() (
(![]() ) ) ∙
) ) ∙ ![]() (
(![]() ) називається число (скаляр)
) називається число (скаляр)
![]() ·
· ![]() =
= ![]() . (3)
. (3)
№5. Знайдіть ![]() ·
· ![]() , якщо
, якщо ![]() (-2; 3; 1),
(-2; 3; 1), ![]() (-4; -5; 2).
(-4; -5; 2).
Розв’язування.
![]() ·
· ![]() =-2
=-2![]()
№6. Дано вектори ![]() (2; -1; 4),
(2; -1; 4), ![]() (5; 3; n). При якому значенні п скалярний добуток векторів дорівнює -3?
(5; 3; n). При якому значенні п скалярний добуток векторів дорівнює -3?
 Розв’язування.
Розв’язування.
![]() ·
· ![]() =2
=2![]() ;
;
10-3+4n=-3;
4n= -10;
n= -2, 5
Із означення скалярного добутку двох векторів ![]() і
і ![]() випливають його властивості:
випливають його властивості:
1) ![]() ·
· ![]() =
= ![]() ·
· ![]() .
.
2) (![]() +
+ ![]() ) ·
) · ![]() =
= ![]() ·
· ![]() +
+ ![]() ·
· ![]() .
.
3) Скалярний добуток векторів ![]() і
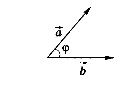
і ![]() дорівнює добутку їх абсолютних величин на косинус кута між ними (рис. 297):
дорівнює добутку їх абсолютних величин на косинус кута між ними (рис. 297):
![]() ·
· ![]() =
= ![]() ·
· ![]() cos φ (4)
cos φ (4)
Наслідки із властивості 3:
1) 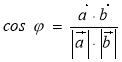
2) Два відмінні від нуля вектори ![]() і
і ![]() перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
3. Кут між векторами, що задані своїми координатами. Умова ортогональності векторів. Приклади.
Як видно було із наслідка з властивості 3 скалярного добутку: 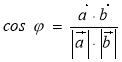
Якщо дану рівність записати у координатному вигляді, то:
![]()
![]() (5)
(5)
№7. Знайдіть ![]() ·
· ![]() , якщо
, якщо ![]() = 5,
= 5, ![]() = 4, а кут між векторами дорівнює 120°.
= 4, а кут між векторами дорівнює 120°.
№8. Чи перпендикулярні вектори ![]() (2; 3; 6) і
(2; 3; 6) і ![]() (3; 2; -1)?
(3; 2; -1)?
№9. При якому значенні m вектори ![]() (6; 0; 12) і
(6; 0; 12) і ![]() (-8; 13; m) перпендикулярні?
(-8; 13; m) перпендикулярні?
№10. Чи є серед векторів ![]() (2; 3; 1),
(2; 3; 1), ![]() (5; 9; 2),
(5; 9; 2), ![]() (-3, 1; 3) ортогональні вектори?
(-3, 1; 3) ортогональні вектори?
№11. Знайдіть кут між векторами ![]() (1; 1; 0) і
(1; 1; 0) і ![]() (1; 0; 1).
(1; 0; 1).
№12. Знайдіть cos ABC, якщо А(1; -3; 4), В(2; -2; 6), С(3; 1; 3).
VI. Узагальнення та систематизація знань, умінь та навичок студентів.
Бесіда за матеріалами заняття.
1) Як визначається довжина вектора в координатному вигляді?
2) Чому дорівнює скалярний добуток векторів, які задано координатами?
3) Як можна обчислити скалярний добуток векторів, якщо відомі їх довжини і кут між ними?
4) Як можна визначити косинус кута між двома ненульовими векторами?
5) Сформулюйте ознаку перпендикулярності двох ненульових векторів.
6) У просторі дано вектори ![]() (1; 1; 0),
(1; 1; 0), ![]() (0; 1; 1). Укажіть, які з вказаних тверджень правильні, а які — неправильні:
(0; 1; 1). Укажіть, які з вказаних тверджень правильні, а які — неправильні:
а) довжини векторів ![]() і
і ![]() рівні;
рівні;
б) скалярний добуток векторів ![]() і
і ![]() дорівнює 2;
дорівнює 2;
в) кут між векторами ![]() і
і ![]() дорівнює 120°;
дорівнює 120°;
г) (![]() +
+ ![]() )(
)(![]() –
– ![]() ) = 0;
) = 0;
д) вектори ![]() +
+ ![]() і
і ![]() –
– ![]() перпендикулярні.
перпендикулярні.
Робота з підручником
VІI. Рефлексія Оцінювання
VII. Домашнє завдання
1.Скласти кросворд до теми ”Координати та вектори” (для всіх бажаючих покращити оцінку за тему).
2. Виконати вправи:
№1. Дано точки А (1; 0; - 2), В (-2; 1; 3) і вектор ![]() (1; 0; - 2) . Знайдіть:
(1; 0; - 2) . Знайдіть:
а) координати вектора ![]()
б) абсолютну величину вектора ![]()
в) координати суми векторів ![]() і
і ![]() .
.
№2. Знайдіть довжину вектора 2![]() +3
+3![]() , якщо
, якщо ![]() (3; 1; 0),
(3; 1; 0), ![]() (0; 1; -1).
(0; 1; -1).
№3. Знайдіть косинус кута С трикутника АВС, якщо А(0; 1; - 1), В (1; - 1; 2),
С (3; 1; 0).
3.Повторити все про рівняння прямої на площині.




про публікацію авторської розробки
Додати розробку
