Конспект уроку на тему "Графічний спосіб задання функції. Графік функції"

Урок №47        Дата ___________

Тема: Графічний спосіб задання функції. Графік функції

Мета:

Навчальна: домогтися засвоєння знань про функцію та методи її задання, поглибити знання учнів про графічний метод задання функції, навчити розв’язувати завдання користуючись графіком функції.

розвинути просторову уяву, логічне мислення.

виховувати зібраність, комунікативність, вміння концентрувати свою увагу, розуміння ролі математики в житті, розуміння важливості математичних знань.

Обладнання: Підручник з математики 7 клас (Мерзляк), Збірник задач і контрольних робіт з алгебри 7 клас (Мерзляк

Тип уроку: засвоєння нових знань.

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

3. Формулювання мети й завдань уроку, мотивація навчальної діяльності

На попередніх уроках ми розглядали таке поняття як функція та деякі способи її задання. Сьогодні ми удосконалимо свої знання з даної теми та детально розглянемо ще один спосіб задання функції.

4. Актуалізація опорних знань

Бліц опитування.

1. Що таке функція?
2. У записі y=2x+3 вказати залежну і незалежну змінні.
3. Що таке область визначень функції?
4. Що таке область значень функції?
5. Які способи задання функцій ви знаєте?
6. Що таке координатна площина?

5. Засвоєння нових знань

Розглянемо функцію y=x²–4x, де −1≤x≤4. Складемо таблицю значень цієї функції при цілих значеннях аргументу:

Розглянемо пари чисел, записаних у кожному стовпці цієї таблиці, як координати (x; y) точок координатної площини. При цьому значення аргументу є абсцисою точки, а відповідне значення функції — її ординатою. Зобразимо ці точки на рисунку.

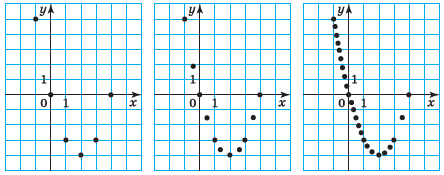
Якщо х надавати інших значень із нашого відрізка, то можна отримати більше точок на координатній площині. З’єднавши ці точки отримаємо графік функції.

О. Графіком функції f називають геометричну фігуру, що складається з усіх тих і тільки тих точок координатної площини абсциси яких = значенню аргументу, а ординати – відповідним значенням функції f.

Даний процес є досить тривалим і не точним, адже точок які необхідно нанести на координатну площину безліч, тому при з’єднанні знайдених точок побудова є не точною. Зараз існує безліч програм та онлайн-сервісів які будують графіки функцій з великою точністю. Вашим домашнім завданням на наступний урок буде обрати один із цих сервісів та побудувати в ньому графік функції y=x², зробити скріншот та роздрукувати, побудувати за допомогою таблички даний графік вручну. Порівняти отримані результати.

Графік функції не обов’язково має бути лінією.

Маємо функцію задано таблично

Графік даної функції складається з 2 точок

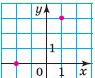
Розглянемо приклад побудови графіка функції, заданої описом. Нехай область визначення даної функції — усі числа. Для кожного додатного аргументу значення функції дорівнює 1; для кожного від’ємного аргументу значення функції дорівнює –1; якщо аргумент дорівнює нулю, то значення функції дорівнює нулю. Графік цієї функції зображено на дошці. Він складається з трьох частин: точки O (0; 0) і двох променів, у кожного з яких «виколото» початок.

Не будь-яка фігура, зображена на координатній площині, може слугувати графіком функції. Наприклад, коло не може бути графіком функції, оскільки за заданим значенням змінної x не завжди однозначно знаходиться значення змінної y.

Фігура, зображена на координатній площині, може бути графіком функції, якщо будь-яка пряма, перпендикулярна до осі абсцис, має із цією фігурою не більше ніж одну спільну точку. Можна говорити, що ця фігура задає деяку функцію. Такий спосіб задання функції називають графічним. Абсциси й ординати всіх точок цієї фігури утворюють відповідно область визначення та область значень функції.

Якщо функцію задано графічно, то значення функції за заданим значенням x₀ аргументу можна знайти за таким правилом:

через точку (x₀; 0) провести пряму, перпендикулярну до осі абсцис, а потім знайти ординату точки перетину цієї прямої з графіком. Знайдена ордината дорівнює f (x₀)

Вивчаючи графік можна, наприклад, знайти:

1) область визначення функції

2) область значень функції

3) значення аргументу, при яких значення функції дорівнює нулю

4) значення аргументу, при яких функція набуває додатних значень

5) значення аргументу, при яких функція набуває від’ємних значень.

Після вивчення цього  стає зрозумілим, чому в техніці, медицині, економіці та багатьох інших сферах людської діяльності так широко використовують комп’ютерні програми, які дозволяють будувати графіки різноманітних функціональних залежностей.

Розглянемо приклади.

Приклад 1. Чи належить графіку функції y=x²+1 точка А(0;1). В(2;15)

х=0
y=0²+1
Точка А належить графіку функції.

x=2
y=2²+15=19
Точку В не належить графіку функції

Методичний коментар: Якщо т належить графіку ф то її координати при підставлені у формулу, що задає функцію утворюють правильну числову рівність. Тому у функцію замість х підставляємо абсцису т і шукаємо у. далі порівнюємо знайдений у із ординатою т, якщо вони рівні то точка належить графіку, якщо ні – не належить.

Приклад 2. Не виконуючи побудови, знайдіть координати точок перетину графіка функції y=x²–4 з осями координат.

x=0
y=0²-4=-4
(0;-4) - точка перетину з віссю Оу

у=0
х²-4=0
х²=4

х=+-2

(-2; 0), (2; 0) – т перетину з віссю Ох.

Методичний коментар: Якщо графік ф перетинає осі координат, то одна з координат точок перетину – 0. Якщо графік перетинає вісь Оу то координата по х=0, якщо графік ф перетинає вісь Ох то координати по у=0. Щоб знайти точки перетину слід замість х/у підставити 0 і розв’язавши рівняння знайти у/х, потім записати утворені т.

6. Вправи для закріплення

Індивідуальна робота біля дошки.

№ 822 (Алгебра 7 клас Мерзляк)

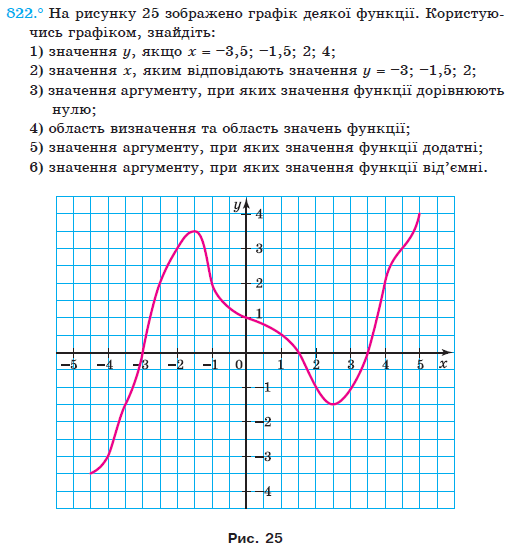
Розв'язання:

1. y=-1,5; 3,5; -1; 2.
2. х=-4; -3,5 і 2,5; -2,5 і -1 і 4.
3. -3; 1,5; 3,5
4. -4,5 – 5
   -3,5 – 3,5
5. -3 – 1,5 і 3,5 – 5.
6. -4,5 - -3 і 1,5 – 3,5.

Методичний коментар: 1) для того щоб знайти значення у якщо відомо х через точку з координатою (х; 0) на осі Ох проводимо пряму перпендикулярну до осі Ох, шукаємо її перетин із графіком функції, знаходимо ординату отриманої точки.

2) для того щоб знайти значення х якщо відомо у через точку з координатою (0; у) на осі Оу проводимо пряму перпендикулярну до осі Оу, шукаємо її перетин із графіком функції, знаходимо абсцису отриманої точки.

3) якщо значеннч функції = 0, то графік функції перетинає вісь Ох, тому шукаємо абсциси т перетину графіку функції з віссю Ох.

4) Область визначень – всі значення х при яких функція існує.
Область значень – всі значення у при яких функція існує.

5) Додатні значення ф відповідають додатнім значенням на осі Оу. Тому слід знайти всі х при яких графік функції знаходиться над віссю Ох.

6) Від'ємні значення ф відповідають відємним значенням на осі Оу. Тому слід знайти всі х при яких графік функції знаходиться під віссю Ох.

№ 157 (Збірник задач 7 клас Мерзляк)

1. x=0
   y=0²-0+1=1
   Точка А не належить графіку функції
2. x=0
   y=0²-0+1=1
   Точка В належить графіку функції.

(3-5 аналогічно)

Методичний коментар: Якщо т належить графіку ф то її координати при підставлені у формулу, що задає функцію утворюють правильну числову рівність. Тому у функцію замість х підставляємо абсцису т і шукаємо у. далі порівнюємо знайдений у із ординатою т, якщо вони рівні то точка належить графіку, якщо ні – не належить.

№ 825 (Алгебра 7 клас Мерзляк)

1. (0; -4), (1; 3)
2. (0; 1), (1; 2)
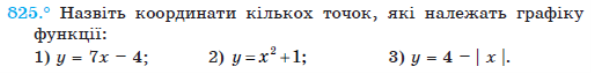
3. (0; 4), (1; 3)

Методичний коментар: Якщо т належить графіку ф то її координати при підставлені у формулу, що задає функцію утворюють правильну числову рівність. Тому обираємо довільний х, підставляємо його у функцію, знаходимо у, отримані х та у і є координатами точки на графіку даної ф.

7. Підбиття підсумків уроку

• Що нового ви дізналися сьогодні на уроці?
• Що було для вас уже відомим?
• Що було цікавим на уроці?
• Над чим ще варто попрацювати?

8. Домашнє завдання

§ 22 № 823, 824, 828.