конспект уроку на тему "Лінійна функція"
1
Мета:
Навчальна: Удосконалити знання означення та властивостей лінійної функції; розглянути залежність розміщення графіка лінійної функції в системі координат від значень коефіцієнтів та взаємне розміщення графіків двох лінійних функцій.
Розвиваюча: Розвивати навчальні інтереси, здібності на основі розумових дій; формувати навички аналізу, систематизації, узагальнення.
Виховна: Виховувати активну позицію в навчанні і житті; сприяти розвитку математичної культури учнів; формувати навички спільної діяльності.
Тип уроку: удосконалення знань і вмінь.
Обладнання: Роздатковий матеріал, сигнальні картки, проектор, мультимедійний екран.
Структура уроку;
|
№з/п |
Етапи уроку |
Час, хв |
|
1 |
Організаційний |
2 |
|
2 |
Перевірка виконання домашнього завдання |
5 |
|
3 |
Оголошення теми і мети уроку |
1 |
|
4 |
Актуалізація опорних знань |
7 |
|
5 |
Удосконалення знань |
6 |
|
6 |
Удосконалення вмінь |
13 |
|
7 |
Домашнє завдання |
3 |
|
8 |
Підсумок уроку |
3 |
Хід уроку
1.Організаційний
Вітаюся. Перевіряю готовність учнів до уроку, налаштовую їх на роботу.
2.Перевірка домашнього завдання
А зараз ми подивимося яких успіхів ви досягли, виконуючи домашнє завдання. Виберіть правильну на вашу думку відповідь.
1.Яка з поданих функцій є лінійною?
а)
; б)
; в) 
; г) 
.
2.Чому дорівнює коефіцієнт k у функції, яка задана формулою 
?
a) 
; б) 
; в) 
; г) 
3.Графіком будь-якої лінійної функції є:
а) замкнена лінія; б) пряма; в) коло; г) довільна крива.
4.Областю визначення лінійної функції є:
а) усі додатні числа; б) усі від’ємні числа;
в) усі числа; г) усі числа, крім нуля.
5.Областю значень лінійної функції є:
а) усі додатні числа; б) усі від’ємні числа;
в) усі числа; г) усі числа, крім нуля.
6.Учень мав у грн. За ці кошти він придбав х олівців по 1,5 грн кожен, після чого в нього залишилося 30 грн. Задайте формулою залежність у від х.
а) 
; б) 
; в) 
; г)
7.Дано лінійну функцію 
. Знайдіть значення у, якщо х=
4.
а) у=5; б)у=11; в)у=3; г)у=9.
8.Дано лінійну функцію . Знайдіть значення х, при якому у
а) 
; б) 
; в) 
; г) 
.
9.Яка з точок належить графіку функції 
а) (0;-4); б) (2;3); в) (2;6); г) (-2;3).
10.Знайдіть область визначення функції 
а) усі числа; б) усі числа, крім нуля;
в) усі числа, крім 5; г) усі додатні числа.
11.Знайдіть область значень функції
а) усі числа; б) усі числа, крім нуля;
в) усі числа, крім 5; г) усі додатні числа.
12.Дано функцію 
. Знайти нулі функції.
а) 
; б) 
; в) 
; г)
;
3.Оголошення теми та мети уроку:
На попередніх уроках ми з вами розглянули загальні відомості про функцію, її властивості та графік, почали знайомство з лінійною функцією. Сьогодні на уроці ми продовжуємо вивчати лінійну функцію і:
- узагальнимо наші знання про лінійну функцію;
- будемо вчитися читати її графік, будувати графік лінійної функції;
- визначатимемо взаємне розміщення графіків двох лінійних функцій, побудованих в одній системі координат;
4.Актуалізація опорних знань:
а) Давайте всі разом розшифруємо народну мудрість, зашифровану на дошці. У кожного з вас є картка, на якій вказано координати точок. Знайдіть її в координатній площині і дізнаєтесь літеру (Букви в координатній площині українські). Назвіть номер своєї картки і літеру, що ви знайшли.
Перед розв’язком:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
|
12 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Після розв’язку:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
|
12 |
13 |
|
М |
У |
Д |
Р |
И |
М |
Н |
І |
Х |
Т |
О |
Н |
Е |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
В |
Р |
О |
Д |
И |
В |
С |
Я |
А |
Н |
А |
В |
Ч |
И |
В |
С |
Я |
б) Інтерактивна вправа «Світлофор». Використати сигнальні картки. Сформулювати питання так, щоб були тільки відповіді «так»- зелені або «ні» - червоні картки.
Задані функції:
1)
; 2) 
; 3) 
; 4) 
; 5) 
- Чи дана функція є лінійною?
- Коефіцієнт заданої функції дорівнює 2?
- Область визначення даної функції множина дійсних чисел?
- Графік функції проходить через початок координат?
5.Удосконалення знань
Розглянемо кілька функцій і охарактеризуємо розташування їх графіків у системі координат: 
, 
, 
, 
, 
.
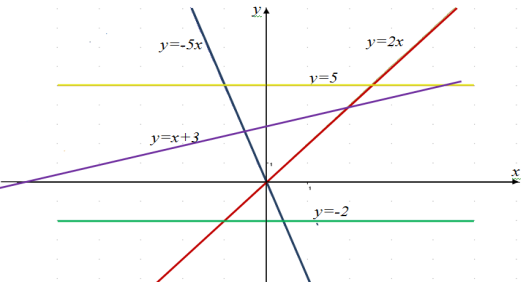
Зробимо загальний висновок:
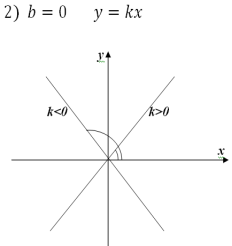
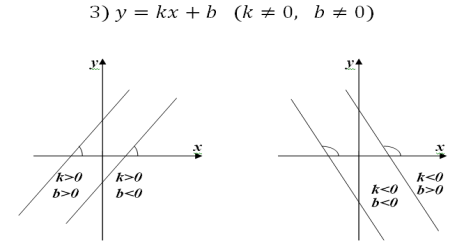
Залежність між розташуванням прямої y=kx+b
та значеннями k і b
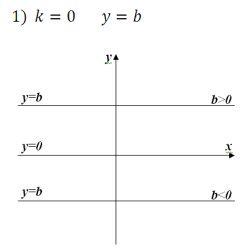
Давайте побудуємо графіки лінійних функцій, у яких є однакові коефіцієнти.
Наприклад, 
.
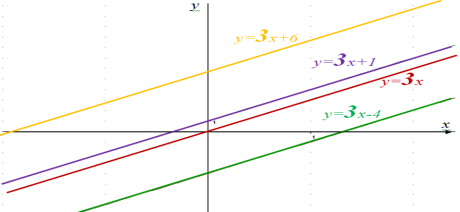
Бачимо, що графіки цих функцій – паралельні прямі.
Побудуємо графіки наступних функцій:
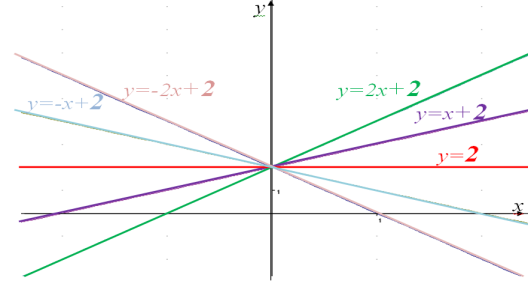
Бачимо, що всі графіки перетинаються в одній точці.
Якщо ж коефіцієнти у функцій різні, то дві прямі перетинатимуться в одній точці.
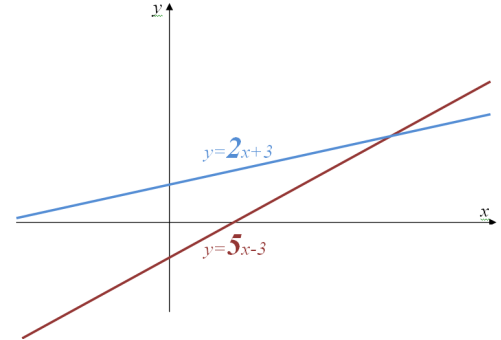
6.Удосконалення вмінь
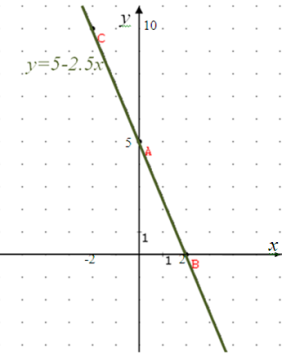
796.Накресліть графік функції y=5-2.5x. За графіком знайдіть:
а) значення функції, якщо значення аргументу дорівнює 2;
б) значення аргументу, якщо значення функції дорівнює 10;
в) значення аргументу, при яких функція набуває додатних значень;
г) нулі функції;
д) точки перетину графіка з осями координат.
Розв’язання
а) Якщо х=2, то у=0. г) у=0 при х=2.
б) Якщо у=10, то х=-2. д) В (2;0), А(0;5)
в) у>0 при х<2
798.Знайдіть значення k, якщо графік функції y=kx-2 проходить через точку (6;-11).
Розв’язання
-11=6k-2; 6k=-11+2; 6k=-9; k=-9:6; k=-1.5
Відповідь: -1,5.
800.Не виконуючи побудови, знайдіть координати точок перетину графіка функції з осями координат 
Розв’язання
1,5х-20=0, 1,5х=20, х=20:1,5, х=
Відповідь: (0;-20) і (;0).
Відповідь: (0;5) і (20;0).
809.Установіть відповідність між формулами функцій y=3x; y=-3x; y=x+3 та їх графіками 1-3, зображеними на малюнку.
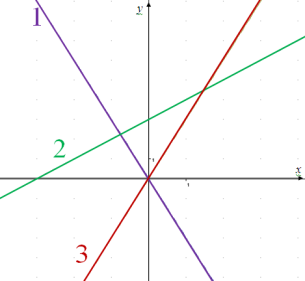
Розв’язання
1- y=-3x;
2- y=x+3
3- y=3x
Задайте формулою функцію, графік якої проходить через точку А(1;4) паралельно графіку функції y=3x-1.
Розв’язання
Запишемо загальний вигляд лінійної функції 
Якщо графіки паралельні, то k=3. Отже, маємо рівняння: 4=3*1+b, b=4-3, b=1. Отже, функція задана формулою 
.
7.Домашнє завдання
Опрацювати §21
Виконати завдання: №797, 799, 801
8.Підсумок уроку
Узагальнення результатів діяльності на уроці.
Поділіться, що нового ви дізналися на уроці, які отримали враження, емоції від нашого сьогоднішнього уроку.
Інтерактивна вправа «Незакінчене речення». (Учні висловлюються по черзі, починаючи речення зі слів, записаних на дошці)
На цьому уроці….
Для мене було….
Я навчився….
Я дізнався….
про публікацію авторської розробки
Додати розробку