Урок 3

Тема уроку.   Многогранник та його елементи. Опуклі многогранники. Призма.

Мета уроку:   формування понять многогранник; ребра, грані, вершини многогранників; опуклий многогранник: призма; основи і бічні грані, ребра призми; висота призми; поверхня та бічна поверхня призми; вивчення властивостей граней та бічних ребер призми.

Обладнання: моделі многогранників.

Перевірка домашнього завдання

1. Обговорення розв'язування задачі № 3 за записами, зробленими на дошці до початку уроку.

Розв’язання задачі № З

Нехай SA, SB, SC — ребра тригранного кута (рис. 17), <ASC = γ.

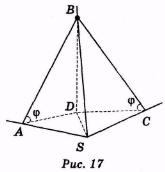Проведемо BD(ASC), ADAS. DCSC, тоді ABAS, BCCS, отже, <BAD і <BCD — лінійні кути двогранних кутів з реб­рами SA і SC: <BAD=<BCD=φ.

ΔADB = ΔCDB, тому AD = DC. Якщо АВ = а, то AD = acosφ, BD = asinφ.

ΔΑDS = ΔCDS, тому <ASD = <CSD =. Із трикутника ASD ,  .

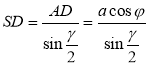ΔΑΒS = ΔCΒS, отже, α = <ASB = <CSB. Із трикутника АВS

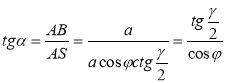, тоді .

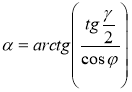Оскільки SD — проекція SВ на (ACS), то <BSD — кут між ребром SB і площиною ASC: β = <BSD . Із трикутника BSD

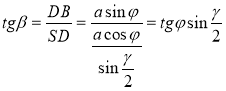, тоді .

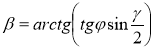Відповідь. , .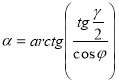

Під час обговорення можливі такі запитання до класу:

1) Чому АВАS, BCCS?

2) Поясніть, чому <BAD і <BCD — лінійні кути двогранних кутів з ребрами SА і SC.

3) За якою ознакою ΔADB = ΔCDB ?

4) Як одержали значення AD і BD?

5) Чому <ASD = <CSD = ?

6) Сформулюйте правила, згідно з якими знайдено AS і SD.

7) Чому ΔАВS = ΔСВS?

8) Чому дорівнює tgα?

9) Що називається кутом між прямою і площиною?

10) Чому дорівнює кут, який утворює площина кута у з протилежним ребром?

2. Самостійна робота.

Варіант 1

1. Кут АВС — лінійний кут двогранного кута з ребром b. Яке взаємне розмі­щення прямих b і АB? (5 балів)

2. Двогранний кут дорівнює α. На одній із граней дано точку, яка знаходиться на відстані d від другої грані. Знай­діть відстань від цієї точки до ребра кута. (7 балів)

Варіант 2

1. Кут АВС — лінійний кут двогранного кута з ребром b. Яке взаємне розміщення прямої b і площини АВС? (5 балів)

2. Двогранний кут дорівнює α. На одній із граней дано точку, яка знаходиться на відстані d від ребра кута. Знайдіть відстань від цієї точки до другої грані. (7 балів)

Варіант 3

1. Кут АВС — лінійний кут двогранного кута з ребром b. Яке взаємне розміщення прямих b і ВС? (5 балів)

2. Точка, взята на одній із граней гострого двогранного кута, знахо­диться від ребра на відстані α, а від другої грані — на відстані b. Знайдіть величину двогранного кута. (7 балів)

Варіант 4

1. Кут АВС — лінійний кут двогранного кута з гранями α і β. Яке взаємне розміщення площини АВС і площини α ? (5 балів)

2. Двогранний кут дорівнює α. На одній грані взято точку і проведено з неї перпендикуляр до другої грані. Знайдіть довжину перпендикуляра, якщо основа перпендикуляра знаходиться на відстані d від ребра. (7 балів)

Відповідь.  Варіант 1. 1) bАВ; 2) .

Варіант 2. 1) b(АВС); 2) d sinα.

Варіант 3. 1) b(ВС); 2) arcsin.

Варіант 4.1) (АВС) α; 2) dtgα.

II. Сприйняття та усвідомлення нового матеріалу

Многогранники та їх елементи, опуклі многогранники

Фігури, які вивчає стереометрія, називаються тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежену по­верхнею. Демонструємо моделі многогранників.

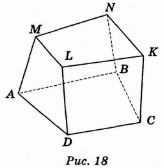
Многогранником називають тіло (частина простору), обмежене скінченою кількістю плоских многокутників (рис. 18).

Многокутники, які обмежують многогранник, називають його гра­нями, їх сторони — ребрами, а вершини — вершинами многогранника.

На рис. 18 гранями е многокутники: ABCD, AMLD, DLKC, BCKN, ABNM, MNKL; ребрами — сторони AD, DC, ВС, АВ, КС, LD, AM, NB, ML, LK, NK, MN; вершинами —точки А, В, C, D, Μ, Ν, Κ, L.

Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні.

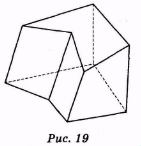
Прикладами опуклих многогранників можуть бути куб, прямокут­ний паралелепіпед, тетраедр тощо. На рис. 19 зображено неопуклий многогранник.

Демонструємо опуклі і неопуклі многогранники. Многогранники в оточуючому середовищі зустрічаються дуже часто. Цеглина, коробка, шафа, стілець, дошка, кристал — все це моделі многогранників. Знання властивостей многогранників необхідне багатьом фахівцям.

Столяр має справу з многогранниками, вистругуючи бруски, видов­буючи в них прямокутні отвори або заглибини. Муляр кладе стіни, спо­руджуючи  будівлі, у формі многогранників. І тесляри, що зводять гори­ща над будівлями, і екскаваторники, що риють котловани, і мінералоги, кристалографи, гранильники — всі мають справу з многогранниками.

Розв'язування задач

1. Наведіть приклади предметів побуту, що є геометричними тілами.

2. Які із фігур, зображених на рис. 20, є геометричними тілами?

3. Які із зображених на рис. 21 тіл є многогранниками?

4. Наведіть приклади предметів побуту, які мають форму многогранника.

5. Наведіть приклади речовин, вивчених у курсі хімії, кристали яких мають форму многогранника.

Рис. 20

6. Скільки вершин, ребер, граней має:                  

 а) тетраедр;   б) куб?

7. Яке найменше число ребер може мати многогранник?

(Відповідь. 6.)

8. Побудуйте многогранник, який має 4 грані. Скільки ребер і скіль­ки вершин він має? (Відповідь. Ребер — 6, вершин — 4.)

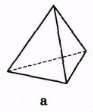
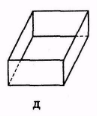
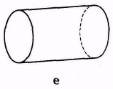
Рис. 21

9. Скільки ребер може сходитися у вершині многогранника?

(Відповідь. Довільне число, але не менше трьох.)

10. Побудуйте многогранник, у якого число вершин і число граней од­накові.

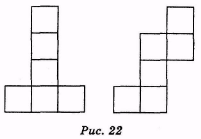
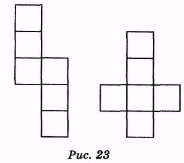
11. Якщо поверхню многогранника розрізати по кількох його ребрах і розкласти на площині, то дістанемо розгортку даного многогран­ника. На рис. 22 подані деякі розгортки куба. Побудуйте розгортку куба, відмінну від поданих. (Відповідь, Рис. 23.)

12. На рис. 24 зображено розгортки многогранників. Визначте, скільки у цих многогранників вершин, граней, ребер. (Відповідь, а) Вершин — 8; граней — 6; ребер — 12; б) вершин — 5, граней — 5, ребер — 8.)

13. Побудуйте многогранник, який має: а) 8 ребер; б) 9 ребер; в) 11 ре­бер. (Відповідь. Рис. 25.)

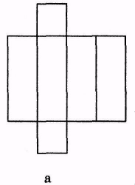
Рис. 24

14. Побудуйте многогранник, який має 5 граней і 5 вершин. Скільки ребер він має? (Відповідь, 8 ребер.)

15. Побудуйте многогранник, який має 5 граней і 6 вершин. Скільки ребер він має? (Відповідь. 9 ребер.)

16. Доведіть, що число плоских кутів многогранника вдвічі більше від числа ребер.

17. Многогранник має 12 ребер. Скільки в нього плоских кутів?

(Відпо­відь. 24 кути.)

Призма

Можна провести пояснення нового матеріалу згідно з п. 40 § 5 під­ручника. Можна дати пояснення нового матеріалу по-іншому.

Многогранник, дві грані якого — рівні n-кутники з відповідно паралельними сторонами, а всі інші n граней — паралелограми, на­зивається n-кутною призмою (рис. 26).

Демонструємо моделі призм.

Її рівні n-кутники називаються основами призми, а паралелогра­ми — бічними гранями, сторони основи — ребрами основи, інші реб­ра — бічними ребрами.

Завдання

Укажіть на моделях призми основи, бічні грані, ребра основи, бічні ребра.

З означення призми випливає, що основи призми рівні, а також ле­жать в паралельних площинах. Бічні ребра паралельні й рівні. Поверх­ня призми складається з основ і бічної поверхні.

Площею поверхні призми називається сума площ усіх її граней. Оскільки основи рівні, то:               S_пр = S_{біч.пов} ⁺ 2S_ocн,

де S_пр — площа поверхні призми;

S_{біч.пов} — площа бічної поверхні призми;

S_осн – площа основи.

Висотою призми називається відстань між площинами її основ. Відрізок, який сполучає дві вершини призми, що не належать одній і рані, називається діагоналлю призми.

Розв'язування задач

1. Скільки граней має n-кутна призма? Чи може призма мати 101 грань?

(Відповідь. n+2;так.)

2. Скільки ребер має n-кутна призма? Чи може призма мати 101 реб­ро?

(Відповідь. 3n; ні.)

3. Скільки вершин має n-кутна призма? Чи може призма мати 101 вершину?

(Відповідь. 2n; ні.)

4. Призма має 20 граней. Який многокутник лежить в ЇЇ основі?

(Від­повідь. 18-кутник.)

5. Назвіть предмети побуту, які мають форму призми.
6. а) Скільки діагоналей можна провести в чотирикутній; п'ятикут­ній;         n-кутній призмі?

б) Чи існує призма, яка не має діагоналей?

(Відповідь, а) 4; 10; (n - 3)n; б) існує: трикутна призма.)

7. Знайдіть суму всіх плоских кутів n-кутної призми.

(Відповідь. 720° (n – 1).)

8. Знайдіть суму всіх двогранних кутів n-кутної призми.

(Відповідь. 360° (n – 1).)

9. Три грані призми — квадрати зі стороною 2 см, а дві інші — три­кутники. Накресліть цю призму та її розгортку. Знайдіть площу поверхні призми.

(Відповідь. Рис. 27, 12 + 2 см².)

10. Висота призми дорівнює Н, а бічне ребро нахилене до площини ос­нови призми під кутом α . Знайдіть довжину бічного ребра призми.

(Відповідь..)

11. АВСА₁B₁С₁ — призма, A₁K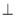(ABC), AK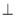ВС (рис. 28). Доведіть, що ΒΒ₁C₁C — прямокутник.

Ρ о з в ' яз а н н я

Оскільки A₁K(ABC) і AKВС, то за теоремою про три перпен­дикуляри А₁АВС. Оскільки СС₁ || АА₁ і А₁АВС, то СС₁ВС.

Оскільки ΒΒ₁C₁C — паралелограм і <C₁CB = 90°, то ΒΒ₁C₁C — прямокутник.

12. Основа призми— рівносторонній трикутник, одна з вершин верх­ньої основи проектується в центр нижньої основи. Доведіть, що одна з граней призми — прямокутник.
13.  Основа призми — правильний трикутник АВС. Бічне ребро АА₁ утворює рівні кути зі сторонами основи АС і АВ. Доведіть, що:

а) ВСАА₁; б) СС₁B₁В — прямокутник.

III. Домашнє завдання

§ 5, п. 39, п. 40; контрольні запитання № 6-12; задачі № 9, 11 (с. 77).

IV. Підведення підсумку уроку

Запитання до класу

1) Дайте означення опуклого многогранника.

2) Скільки граней має 15-кутна призма?

3) Скільки діагоналей можна провести в семикутній призмі?