Тема уроку.   Зображення призми і побудова її перерізів.

Мета уроку: формування понять переріз, діагональний переріз призми, а також умінь будувати перерізи призм.

Обладнання: моделі призм.

 І. Перевірка домашнього завдання

Фронтальне опитування

1. Що таке многогранник? Що називається гранями, ребрами, верши­нами многогранника?
2. Які многогранники називаються опуклими?
3. Дайте означення призми.
4. Призма має n граней. Який многокутник лежить в її основі?
5. Скільки діагоналей можна провести з однієї вершини в трикутній; чотирикутній; n-кутній призмі?
6. Скільки плоских кутів у п'ятикутній призмі? Скільки двогранних кутів? Скільки тригранних кутів? (Відповідь. 30; 15; 10.)
7. У трикутній призмі із двогранних кутів між бічними гранями два кути дорівнюють 20° і 120°. Знайдіть третій кут.
8. Бічне ребро призми дорівнює l і нахилене до площини основи під кутом α · Знайдіть висоту призми.
9. Чи існує призма, у якої тільки одне бічне ребро перпендикулярне до площини основи? Відповідь обґрунтуйте.
10. Чи існує призма, у якої тільки одна грань перпендикулярна до пло­щини основи? Відповідь обґрунтуйте.

II. Сприйняття та усвідомлення нового матеріалу

Правила зображення призми

Зображення призми зручно починати із зображення однієї із її ос­нов. Треба нагадати учням правила зображення многокутників, які ви­вчали в 10 класі;

• зображенням трикутника (рівностороннього, рівнобедреного, пря­мокутного) є довільний трикутник;
• зображенням паралелограма (прямокутника, ромба, квадрата) є до­вільний паралелограм;
• зображенням трапеції (рівнобічної, прямокутної) є трапеція, у якої відношення довжин основ дорівнює відношенню довжин основ зо­бражуваної трапеції;
• зображенням довільного чотирикутника (не паралелограма і не тра­пеції) є довільний чотирикутник;
• зображенням правильного шестикутника є шестикутник, у якого три пари протилежних сторін попарно рівні.

Після побудови зображення основи зображають бічні ребра у вигляді паралельних і рівних відрізків і з'єднують послідовно їх вільні кінці.

Слід визначити, що невидимі ребра зображають штриховими лінія­ми. Для більшої наочності рисунка висоту призми, а також бічні ребра призми, які перпендикулярні до основи, будемо зображати “вер­тикальними відрізками”.

Виконання вправ

1. Побудуйте чотирикутну призму, в основі якої лежить рівнобічна трапеція з основами 1 і 3 см, а бічні ребра перпендикулярні до ос­нови призми.
2. Побудуйте трикутну призму, у якої бічні ребра не перпендикулярні до площини основи призми. Проведіть висоту призми.
3. Побудуйте трикутну призму, у якій одна із вершив верхньої основи проектується в центр кола, вписаного в нижню основу призми.

Правила побудови перерізів призми

У стереометрії часто доводиться розглядати перерізи тіл, зокрема многогранників, різними площинами.

Перерізом опуклого многогранника є опуклий плоский много­кутник.

Його вершини в загальному випадку е точками перетину січної пло­щини з ребрами многогранника, а сторони — відрізками, по яких січна площина перетинає грані многогранника.

Переріз призми площиною, яка проходить через два бічні ребра, які не належать одній грані, називається діагональним перерізом призми (рис. 29).

Виконання вправ

1. Скільки діагональних перерізів можна провести в л-кутній призмі (n > 3) ?

(Відповідь. .)

2. Доведіть, що діагональні перерізи призми — паралелограми.
3. Доведіть твердження: якщо діагональні перерізи призми перетина­ються, то їх спільний відрізок паралельний бічному ребру.

Способи задання перерізу досить різноманітні, і універсального ме­тоду їх побудови не існує. Найбільш ефективними методами є метод слі­дів і метод внутрішнього проектування. Розглянемо кожний з них.

МЕТОД СЛІДІВ

У загальному випадку площина перерізу має спільну пряму з пло­щиною кожної грані многогранника. Пряму, по якій січна площина пе­ретинає площину якої-небудь грані многогранника, називають слідом січної площини. Зрозуміло, що січна площина має стільки слідів, скіль­ки площин граней вона перетинає.

Суть методу слідів полягає в:

1) побудові ліній перетину (сліду) січної площини з площиною грані;

2) знаходженні точок перетину січної площини з ребрами многогранника;

3) побудові перерізу.

Далі слід розглянути приклади побудови перерізів призми з п. 41 § 5 підручника та розв'язати задачу.

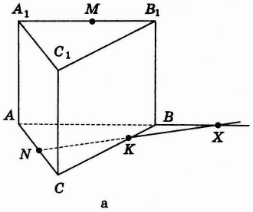
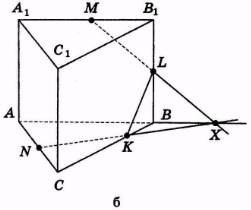
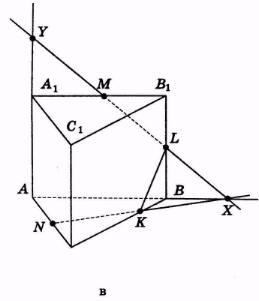
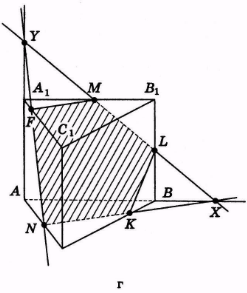
Рис. 31

Задача

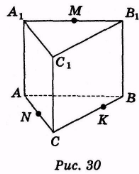
Побудуйте переріз трикутної призми площиною, що проходить через три точки К, M і N (рис. 30), які належать відповідно ребрам СВ, А₁В₁ і АС.

Розв'язання

NK - слід (MNK) на (АВС).

Знайдемо точку Χ перетину прямої NK і прямої АВ (рис. 31, а). ХМ – слід  (MNK) на (АВВ₁). Знайдемо точку L перетину прямої MX і ребра ВΒ₁ (рис. 31, б).

Знайдемо точку У перетину прямої MX і прямої АА₁ (рис. 31, в). YN — слід (MNK) на (АСС₁). Знайдімо точку F перетину прямої YN і ребра А₁С₁ (рис. 31, г). NKLMF — шуканий переріз.

Розв'язування задач

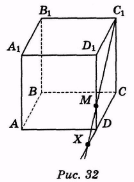
1. Дано куб ABCDA₁B₁C₁D₁ і на його ребрі DD₁ точку М. Знайдіть точку перетину прямої С₁М з площиною основи. (Відповідь. Точка X, рис. 32.)

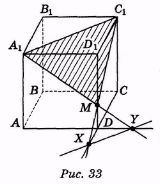
2. Дано куб ABCDA₁B₁C₁D₁ і точку М DD₁. Побудуйте переріз куба площиною, яка проходить через точки Α₁, С₁ і М, та знайдіть лі­нію перетину січної площини з площиною основи куба. (Відповідь. Пряма XY, рис. 33.)

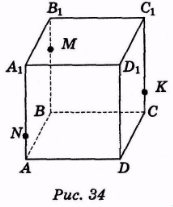
3. Задано чотирикутну призму ABCDA₁B₁C₁D₁. Побудуйте переріз приз­ми площиною MNK, де М ВВ₁, N АА₁, Κ СС₁ (рис. 34).

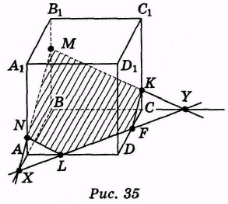
(Від­повідь. NMKFL — шуканий переріз, рис. 35.)

4. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через точки Μ, Ν, Κ— середини ребер A₁B₁, B₁C₁ і СС₁ відповідно.

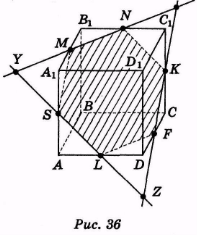
(Відповідь. MNKFLS — шуканий переріз, рис. 36.)

МЕТОД ВНУТРІШНЬОГО ПРОЕКТУВАННЯ

Цей метод застосовується при побудові перерізів у тих випадках, коли не зручно знаходити слід січної площини (наприклад, слід одержується дуже далеко від даної фігури). Розглянемо застосування цього ме­тоду на прикладі.

Задача

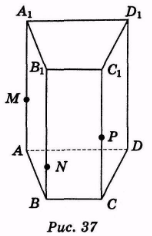
Побудуйте переріз чотирикутної призми площиною, яка проходить че­рез точки Μ, Ν, Р, які належать її бічним ребрам АА₁, ВВ₁, СС₁ (рис. 37).

Розв'язання

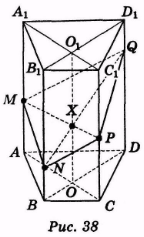
Спроектуємо точки Μ, Ν і Р на площину нижньої основи, одержимо точки А, В, С. У чотирикутнику ABCD проведемо діагоналі АС і BD, які перетинаються в точці О (рис. 38). Через точку О проведемо пряму 00₁ ║ ВВ₁, яка перетинає МР в точці X. У площині BB₁D₁ проведемо пряму NX, яка перетинає ребро DD₁ в точці Q. MNPQ — шуканий переріз.

Суть методу внутрішнього проектування:

1) проектуються дані точки на площину основи, в площині основи бу­дується чотирикутник, у якого три вершини — проекції даних то­чок, а четверта — одна із вершин основи;

2) у площині перерізу будується прообраз точки перетину діагоналей одержаного чотирикутника;

3) будуються точки перетину січної площини з ребрами.

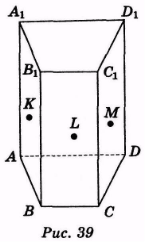
Задача

Точки К, L, Μ лежать на різних гранях довільної чотирикутної при­зми ABCDA₁B₁С₁D₁ причому Κ АВВ₁А₁, L ВСС₁В₁, Μ CDD₁С₁. По­будуйте переріз призми площиною KLM (рис. 39). (Відповідь. Рис. 40.)

III. Домашнє завдання

§ 5, п. 41; контрольні запитання № 13—14; задачі .№5, 7, 10 (с. 77).

IV. Підведення підсумку уроку

Запитання до класу

1. Якою фігурою е діагональний переріз призми? Поясніть, чому.
2. Яка фігура є перерізом призми площиною, паралельною основам? Поясніть, чому.
3. Які методи побудови перерізів вам відомі? У чому їх суть?