Опорні конспекти як засіб підготовки учнів до ЗНО
З метою якісної підготовки до ЗНО я запропонувала учням створити збірку опорних«Опорні конспекти для підготовки учнів до ЗНО»в якому стисло й доступно подано основні теоретичні та практичні поняття математики.























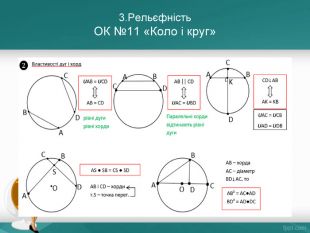
![ОК №5.3. Алгоритм знаходження найбільшого інайменшого значень функції, неперервної на відрізку Кроки. Приклад для функціїY=2x³-3 X² - 36x +5на відрізку[0;4]1. Упевнитися, що заданий відрізок входить до області визначення функції f(x)Знайти похідну f´ (x)f ´(x)=6x² -6x -362. Знайти на даному відрізку критичні точки(точки, в яких f´(x)=0 або не існує) . Вибрати критичні точки, які належать заданому відрізкуf ´(x)=0 якщо х=-2 іякщо х=3 Відрізку [0;4] належить тільки х=33. Знайти значення функції у критичних точках і на кінцях відрізку.f(0)=5f(3)=-76f(4)=-594. З одержаних значень вибрати найбільше та найменше значення.max f(x)=f(0)=5[0;4]min f(x)=f(3)=-76[0;4] ОК №5.3. Алгоритм знаходження найбільшого інайменшого значень функції, неперервної на відрізку Кроки. Приклад для функціїY=2x³-3 X² - 36x +5на відрізку[0;4]1. Упевнитися, що заданий відрізок входить до області визначення функції f(x)Знайти похідну f´ (x)f ´(x)=6x² -6x -362. Знайти на даному відрізку критичні точки(точки, в яких f´(x)=0 або не існує) . Вибрати критичні точки, які належать заданому відрізкуf ´(x)=0 якщо х=-2 іякщо х=3 Відрізку [0;4] належить тільки х=33. Знайти значення функції у критичних точках і на кінцях відрізку.f(0)=5f(3)=-76f(4)=-594. З одержаних значень вибрати найбільше та найменше значення.max f(x)=f(0)=5[0;4]min f(x)=f(3)=-76[0;4]](/uploads/files/2782/53413/57251_images/28.jpg)























































Як якісно підготувати учня до ЗНО?Вчитель. Опрацювати програму ЗНО з математики(20розділів) ;Передати предметні знання та вміння якими повинен володіти учень для складання ЗНО; Навчити розв’язувати завдання з розгорнутою відповіддю згідно критеріїв оцінювання ЗНО;Учень. Готуватись до ЗНО під керівництвом вчителя ;Займатися самоосвітньою діяльністю;Систематично повторювати теоретичний матеріал за допомогою ОК;Віпрацьовувати практичні знання та вміння.
Головна мета та основне завдання ОК «5-11клас» Головна мета опорних конспектів – систематизувати та узагальнити знання з математики;викласти матеріал на доступному рівні; стимулювати процес запам’ятовування. Основне завдання опорних конспектів – розвиток математичної компетентності учнів .
Компетенції учнів та метод ОККомпетентнісний підхід отримання навичок роботи з різними джерелами інформації, аналізу, критичного мислення та вибору головного при складанні ОКРекомендації: під час практичних завдань , с.р. навчального характеру , д.з привчайте користуватись ОК –це веде до розвитку математичної компетентності .
Пам’ятка вчителю для успішного використання методу ОК Заняття слід починати з повторення та перевірки ОК минулого уроку. Перед поясненням нового матеріалу доцільно провести роботу з підручником для первинного осмислення теми. Під час пояснення нового матеріалу створюється ОК . На наступному занятті йде його відтворення (учні заповнюють шаблони) ).
Пам’ятка вчителю для успішного використання методу ОКПісля відтворення ОК доцільно перейти до завдань самостійної роботи для перевірки практичних вмінь учнів. Включати в домашнє завдання ОК. Давати завдання самостійно скласти ОК перед вивченням нової теми. Всі опорні конспекти учні повинні зберігати в папках або зошитах.
Компетентності1)ТЕМА: Застосування похідної до дослідження функцій.ключові- уміння вчитися; спілкуватися державною мовою, розвивати пізнавальний інтерес, навички колективної праці;галузеві- отримання та засвоєння системних знань про застосування похідної до дослідження функцій з використанням відповідного понятійного апарату. предметні - уміти застосовувати набуті знання та вміння для знаходження найбільшого та найменшого значень функції, застосування похідної до знаходження проміжків зростання і спадання функції та екстремумів функції , побудови графіків функцій та розв’язуванні задач. Компетенції з теми записані в програмі з математики для 11 класів в розділі навчальні досягнення учнів , затверджені МОН України
План конференціїМета конференції: Навчитись розв’язувати задачі на знаходження найбільшого та найменшого значень функціїПродовжити підготовку до ЗНО1)Перевірка теоретичних знань;2)Доповідь групи « Економісти»3)Готовність до ЗНО4)Доповідь групи «Фізики»5)Готовність до ЗНО6)Доповідь групи «Архітектори»7)Підсумки конференції
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Дії учнів Дії вчителя1. Повторює ОК №5.1-5.31. Регламентує час, проводить жеребкування, роздає шаблони для перевірки знань.2. Працює в групі над відтворенням ОК2. Організовує та контролює роботу в групах, надає консультації.3. Проводить захист відтворених ОК і рецензує їх.3. Організовує проведення захисту відтворених за шаблоном ОК, надає можливість зробити рецензії учням, які цього бажають.4. Перевіряє правильність заповнення шаблону, виставляє оцінки в картку самоконтролю.4. Виводить ОК на монітор та проводить оцінювання, враховуючи: правильність відтворення шаблона, проведення захисту та надання рецензії.
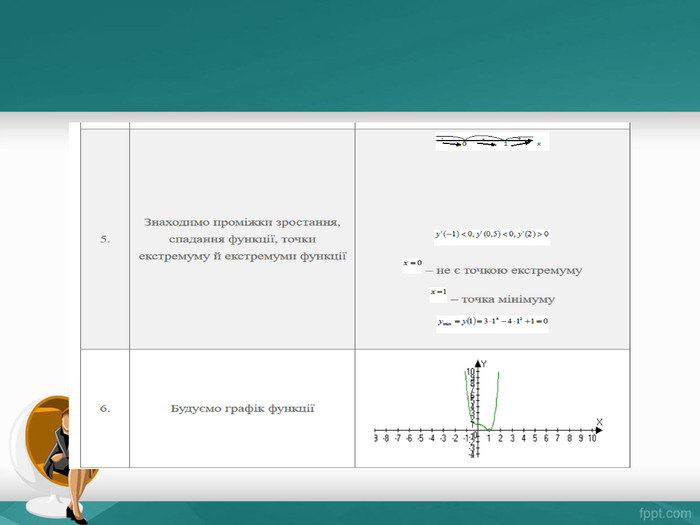
ОК 5.1. «Застосування похідної до знаходження проміжків зростання і спадання функції» Кроки. Приклад для функціїY=2 X³3 X²-36 X+51. Знайти область визначення функції і інтервали на яких функція неперервна. Обл. визначення: RФункція неперервна для X є R2. Знайти похідну функціїf '(x)=6x² 6x-363. Знайти критичні точки (точки, в яких похідна дорівнює нулю або не існує).f(x)=0якщо х= -2,х= 34. У кожному інтервалі, на які область визначення функції розбивається критичними точками, визначити знак похідної і характер зміни функції (за допомогою достатніх умов монотонності)5. Відносно кожної критичної точки визначити чи є вона точкою максимума, мінімума або не є точкою екстремума. Х=-2 точка максимума. Х=3 точка мінімума.6. Записати висновок дослідження функції проміжки монотонності і екстремумиf(x) зростає , якщох є(-∞;-2) і х є( 3;∞) f(x)cпадає, якщо х є(-2;3)Xmax= -2,Ymax=f(-2)=49 Xmin=3, Ymin=f(3)=-76-23+-+f’fx
ОК №5.3. Алгоритм знаходження найбільшого інайменшого значень функції, неперервної на відрізку Кроки. Приклад для функціїY=2x³-3 X² - 36x +5на відрізку[0;4]1. Упевнитися, що заданий відрізок входить до області визначення функції f(x)Знайти похідну f´ (x)f ´(x)=6x² -6x -362. Знайти на даному відрізку критичні точки(точки, в яких f´(x)=0 або не існує) . Вибрати критичні точки, які належать заданому відрізкуf ´(x)=0 якщо х=-2 іякщо х=3 Відрізку [0;4] належить тільки х=33. Знайти значення функції у критичних точках і на кінцях відрізку.f(0)=5f(3)=-76f(4)=-594. З одержаних значень вибрати найбільше та найменше значення.max f(x)=f(0)=5[0;4]min f(x)=f(3)=-76[0;4]
Найбільше і найменше значення функції, неперервної на відрізку Властивість. Якщо функція f(x) неперервна на відрізку і має на ньому скінченне число критичних точок, то вона набуває найбільшого і найменшого значень на цьому відрізку або в критичних точках, які належать цьому відрізку, або на кінцях відрізка.
Знаходження найбільшого і найменшого значень функції, неперервної на відрізку1. Упевнитися, що заданий відрізок входить до області визначення функції f(x)2. Знайти похідну f’(x) 3. Знайти критичні точки: f’(x) = 0 або не існує.4. Вибрати критичні точки, які належать заданому відрізку.5. Обчислити значення функції в критичних точках і на кінцях відрізка. Порівняти одержані значення функції та вибрати з них найменше і найбільше
Знаходження найбільшого або найменшого значення функції, неперервної на інтерваліЯкщо неперервна функція f(x) має на заданому інтервалі тільки одну точку екстремуму х0 і це точка мінімуму, то на заданому інтервалі функція набуває свого найменшого значення в точці х0 . Якщо неперервна функція f(x) має на заданому інтервалі тільки одну точку екстремуму х0 і це точка максимуму, то на заданому інтервалі функція набуває свого найбілшого значення в точці х0
Розв’язання: Рух тіла, кинутого вертикально вгору, здійснюється по прямій. Виберемо напрям руху осі Оу, що збігається з траєкторією руху кулі, з початком руху в точці в момент вильоту кулі зі ствола гвинтівки. З фізики відомо, що рух є рівносповільненим і висота визначається формулою: h(t) = 𝒗𝟎𝐭 − 𝒈𝒕𝟐/2 h = 800t - 10𝒕𝟐/𝟐 = 800t – 5𝒕𝟐
{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі Одну з величин, яку потрібно знайти, позначити через ХВеличину, про яку йдеться, що вона найбільша або найменша, виразити як функцію від ХЦей крок ми пропускаємо, оскільки вже маємо функцію від ХНехай, t=х, тоді h (х)=800х – 5х2{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі Одну з величин, яку потрібно знайти, позначити через ХВеличину, про яку йдеться, що вона найбільша або найменша, виразити як функцію від ХСкористаємося алгоритмом «Задачі на знаходження найбільшого і найменшого значення функції»
{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі 3. Дослідити одержану функцію на найбільше і найменше значення Дослідимо функцію h(х) за допомогою похідної. Похідна h (х)=800х– 5х2 існує при всіх дійсних значеннях Х(отже, h (х) – неперервна функція на заданому проміжку. h’(х)=0, 800-10х=0{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі 3. Дослідити одержану функцію на найбільше і найменше значення
{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі 3. (Продовження)х=80- критична точка + - Знак h’(х) 80 Поведінка h(х)У точці х=80, h’(х) змінює знак з плюса на мінус. Отже, х=80 – точка максимуму. Тобто, при х=t=80с куля підіймається на максимальну висоту.
{69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі 4. Упевнитися, що одержаний результат має зміст для початкової задачі. h(х) = =h(80)=800*80- –5*(80)2=32000 (м){69 C7853 C-536 D-4 A76-A0 AE-DD22124 D55 A5}Назва кроку за алгоритмом. Розв’язання задачі 4. Упевнитися, що одержаний результат має зміст для початкової задачі.
Алгоритм. Упевнитись, що заданий відрізок входить до області визначення функції. Знайти похідну f’(х)Знайти критичні точки f’(x)=0 або не існує. Вибрати критичні точки, які належать заданому відрізку. Обчислити значення функції в критичних точках і на кінцях відрізку. Порівняти одержані значення функції та вибрати з них найбільше і найменше.
Розв'язання Вікно має прямокутну форму. Сума сторін дорівнює півпериметру, тобто 3см. Нехай довжина однієї сторони Х, тоді інша сторона має довжину (3-х). Оскільки довжина сторони додатна, то 0<х<3. Максимальна кількість світла потраплятиме тоді, коли площа вікна максимальна. S = АВ*ВС = х(3-х) = 3х-x2 Дослідимо функцію S(x) за допомогою S’(х)=(3х)’-(x2)′=3−2x
Розв'язання Рух тіла, кинутого вертикально вгору, здійснюється по прямій. Виберемо напрям руху осу Оу, що збігається з траєкторією руху кулі, з початком руху в точці в момент вильоту кулі зі ствола гвинтівки. З фізики відомо, що рух є рівносповільненим і висота визначається формулою: h(t) = 𝑣0t − 𝑔𝑡2/2 h = 800t - 10𝑡2/2 = 800t – 5𝑡2 Дослідимо функцію h(t) за допомогою похідної. h’(t) = 800 – 10t
Існує для всіх t ≥0. Отже, h(t) – неперервна функція на заданому проміжку h’(t)=0 800-10t = 010t = 800t=80 – критична точка. У точці t=80, h’(t) змінює знак з плюса на мінус. Отже, t=80 – точка максимуму. Тобто, при t=80с куля підіймається на максимальну висоту. h = 800 – 10*6400/2 = 64000 – 32000 = 32000(м)
Підведення підсумків коференціїЩо ви чекали від уроку і що отримали?- Які етапи уроку ви вважаєте найбільш вдалими і чому?- Які події викликали яскраві враження?- Чи була користь від такого роду роботи?- В чому ви бачите власні здобутки?- Що вам найбільше вдалося під час уроку?- Які види діяльності були виконані більш вдало?- Вкажіть у порядку спадання основні проблеми і труднощі, які виникли у вас під час уроку. Якими засобами ви їх усували? « мене здивувало..». « урок дав мені для життя ..» « мені захотілося ...»МОЯ ОЦІНКА ЗА РОБОТУ


про публікацію авторської розробки
Додати розробку