Конспект уроку на тему "Площа круга та його частин"

Тема уроку. Площа круга та його частин.

Мета уроку: виведення формули для знаходження площі круга, кругового сектора, кругового сегмента. Формування вмінь учнів застосовувати виведені формули до роз­в'язування задач.

Тип уроку: засвоєння нових знань, умінь і навичок.

 

Хід уроку

І. Організаційний етап.

П-працьовиті

Е-ерудувоні

Р-розумні

Е-енергійні

М-мальовничі

О-оригінальні

Г-грайливі

А-акуратні

 

ІІ. Перевірка домашнього завдання.

Перевірити наявність виконаних домашніх завдань.

Слайд 1.

 

 

 

 

 

 

 

 

 

 

 

 

Слайд 2

 

 

ІІІ. Актуалізація опорних знань.

1. Для повторення вивченого матеріалу , виконаємо вправу “Продовжи речення”

Слайд 3.

 

 

 

 

Слайд 4.

Довжина кола

 

 

Довжина дуги кола

 

2. Дидактична гра  «Вірю -не вірю»

Слайд 5.

• (Учитель зачитує твердження, а учні ставлять «+», якщо воно істинне, або «-», якщо воно хибне)
• 1. Навколо будь-якого трикутника можна описати і в будь-який трикутник можна вписати коло.
• 2. Вписане коло дотикається до усіх сторін правильного многокутника.
• 3. Коло можна описати навколо правильного п-кутника.
• 4. Центри описаного та вписаного кола правильних многокутників  не збігаються
•  5. Центральний кут – це той, який лежить між сторонами многокутника.
• 6..Діаметр удвічі більше  за  радіус.

 

Слайд 6.

 

• Відповіді: 1.+. 2. +. 3.+. 4. -. 5. -. 6.+. ( Взаємоперевірка)

 

 

 

 

 

 

 

 

 

Проблемне завдання

 Слайд 7.

 

Слайд 8 .

 

 

 

 

 

 

 

 

 

 

 

 

Слайд 9.

 

 

 

 

 

 

 

IV. Поетапне сприймання й усвідомлення нового матеріалу

Слайд 10.

 

 

 

Слайд 11.

 

 

Знаходження площі круга

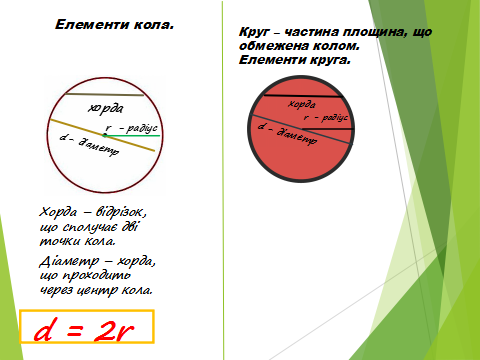
Нагадаємо, що кругом називається частина площини, обмежена колом. Кругом радіуса R з центром у точці О називається точка О і всі точки площини, які містяться від точки О на відстані, не більшій від R.

Круг обмежений колом. Його не можна розбити на многокут­ники і обчислити площу як суму многокутників. Дамо означення площі круга таким чином.

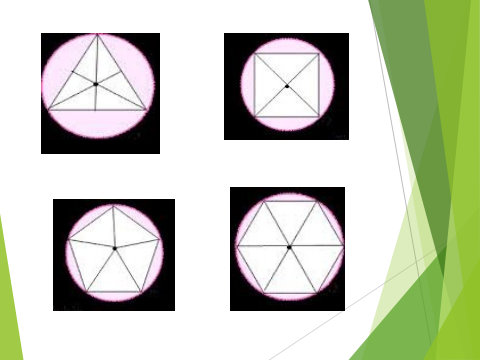
Площею круга називається величина, до якої наближається площа вписаного в це коло правильного многокутника за умови, що число його сторін необмежено збільшується.

Впишемо в коло R правильний п-кутник (рис. 99). Площа правильного многокутника

S_n = nS_ΔAOB = n ∙ r ∙ АВ = Р_пr, де Р_n — пери­метр правильного п-кутника.

При необмеженому збільшенні п площа правильного многокутника S_n наближається до площі круга, Р_п — до довжини кола, r — до R. Отже, одержуємо:

S_кр = CR= ∙ 2πR ∙ R = πR².

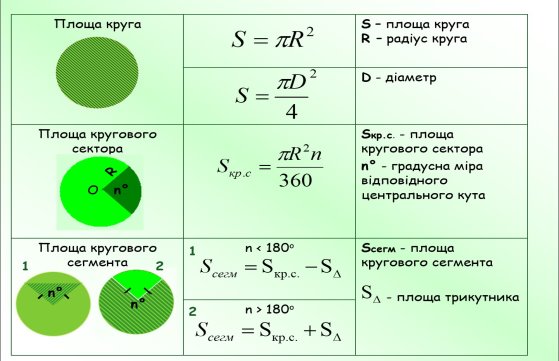
Таким чином, площу круга можна обчислити за формулою S_кр = πR².

Формула дозволяє знаходити площу круга за його радіусом, а також знаходити радіус круга за відомою площею круга.

 

Знаходження кругового сектора

Користуючись формулою площі круга, можна вивести фор­мули для знаходження площі частин круга, зокрема кругового сектора і кругового сегмента.

Круговим сектором називається частина круга, яка лежить усередині центрального кута (рис. 100).

Спираючись на формулу площі круга, виведемо формулу для площі сектора, кутова величина дуги якого дорівнює п° (рис. 101).

  

Площа сектора, кутова величина дуги якого дорівнює 1°, до­рівнює , а площа сектора, кутова величина дуги якого п°, дорівнює , тобто

S_ceк = .

Ця формула пов'язує між собою три величини: S_ceк, R, п, тому за допомогою цієї формули можна знаходити будь-яку одну із цих величин, якщо будуть відомі дві інші.

Знаходження кругового сегмента

Круговим сегментом називається спільна частина круга і пів-площини (рис. 102).

  

Площа сегмента, який дорівнює півкругу, дорівнює . Пло­ща сегмента, який не дорівнює півкругу, обчислюється за форму­лою S_ceгм = ∙ α ± S_Δ, де α — градусна міра центрального кута, який містить дугу кругового сегмента, а S_Δ — площа трикутни­ка з вершинами в центрі круга і на кінцях радіусів, які обмеж­ують даний сектор (рис. 102 і 103). Знак «+» треба брати, якщо α > 180°, а знак «-» — якщо α < 180°.

 

V. Закріплення й осмислення нового матеріалу

 

 

Розв’язування задач

 

№7.3

1. Знайдіть площу круга радіуса 4 см. (Відповідь. 16π см².)

   №7.4

1.     Знайдіть площу круга діаметр якого дорівнює 20 см. (Відповідь.   = .)

№7.27(1)

 

 

№7.32(1)

 

 

 

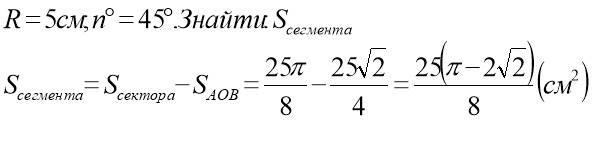
VІ. Підсумок уроку.

Продовжити речення :

На цьому уроці я дізнався 

                              навчився

                               згадав

 

Вид роботи на уроці	Кількість балів
Домашня робота: №7.10 - (1б)                                   №21.27 - (2б)
1. Гра  «  Вірю  -  не  вірю» (3б)
2.  Розв’язування задач.    №7,3---(1 б)                                           №7,4---( 1б)                                           №7,27 (2)---(2б)                                            №7,32 (1)  --- (2 б)
Сума балів                                12б

 

 

 

VІІ. Домашнє завдання

1. Вивчити параграф 2.7 с..64-65,звернути увагу на задачу 2,с.66.
2. Виконати №7.33.

 

 

 

 

 

3. (ЗНО2011)
   
   У прямокутник АВСD, вписано три круги одного й того самого радіуса. Визначити довжину сторони ВС, якщо загальна площа кругів дорівнює 3π

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь:  6см