Допоміжний матеріал «Розв’язання задач на застосування формул для обчислення площі трикутника»

Допоміжний матеріал «Розв’язання задач на застосування формул для обчислення площі трикутника»

Шановні дев’ятикласники!

Сьогодні ми продовжуємо з вами розв’язувати задачі на застосування формул для обчислення площі трикутника.

Задача 1. Бісектриса трикутника ділить його сторону на відрізки 5см і 6 см. Знайти площу трикутника, якщо менша з двох інших сторін 15см.

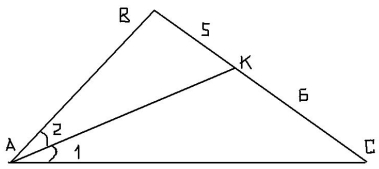
В даному випадку важливо визначити, яка ж зі сторін АВ чи АС є меншою. Як відомо, зовнішній кут трикутника дорівнює сумі двох внутрішніх, з ним не суміжних, тобто:

АКС = 2 + В;

АКВ = 1 + С;

Так як АКС АКВ, то В С, а так як проти більшого кута у трикутнику лежить більша сторона, то АС АВ, тобто АВ = 15см.

Бісектриса кута трикутника ділить його сторону на відрізки, пропорційні до прилеглих сторін: = .

Отже, = , звідки х = (15*6):5=18(см).

Так як у трикутнику відомі всі три його сторони (15см, 11см, 18см), то площу знайдемо за формулою Герона:

р= = 22, тоді S==

=  = 2*11 = 22 (.

В даній задачі ми з вами повторили співвідношення між сторонами і кутами трикутника, властивість бісектриси кута трикутника і застосували формулу Герона для обчислення площі трикутника.

Задача 2.

Знайти найменшу висоту трикутника зі сторонами 7см, 8см, 9см.

Найменшою з висот трикутника є та, яка проведена до найбільшої його сторони (в даному випадку до сторони 9см).

р= = 12, S==

=   =2*6 = 12 (.

S = ah, тоді h = = =  (см).

Бажаю успіху!