Довідничок-помічничок "Готуємось до ЗНО. Подібні радикали. Дії з радикалами"
Даний матеріал допоможе самостійно повторити поняття подібних радикалів та дій з ними. Матеріал містить практичні завдання з розв'язками. завдання для самоперевірки.
Приведення радикалів до найпростішого (нормального) виду.
Для того щоб привести радикал до найпростішого або нормального виду, потрібно виконати послідовно такі операції:
- Спростити підкореневий вираз (якщо це можливо);
- Скоротити показники кореня і підкореневого виразу(якщо вони мають спільний множник);
- Винести з-під радикалу раціональні множники;
- Звільнитись під радикалом від дробів.
Приклади. Привести до найпростішого виду радикали:
а) 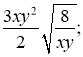 б)
б) 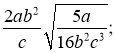 в)
в) ![]()
Розв’язок: a) 
б) 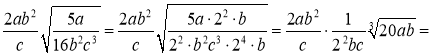
![]() в)
в)![]()
![]()
Два або декілька радикалів називаються подібними, якщо вони однакового степеня і мають однакові підкореневі вирази.
Наприклад. ![]() і
і ![]() – подібні радикали, так як вони обидва третього степеня і мають однакові підкореневі вирази
– подібні радикали, так як вони обидва третього степеня і мають однакові підкореневі вирази ![]() . Інколи радикали стають подібними після деяких перетворень.
. Інколи радикали стають подібними після деяких перетворень.
Приклад 1. Чи подібні радикали: ![]() ?
?
![]()
![]()
![]()
Відповідь: Подібні.
Приклад 2. Чи подібні радикали ![]() і
і ![]() ?
?
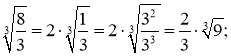
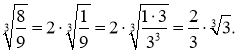
Відповідь: Не подібні.
Приклад 3. Чи подібні радикали:
а)![]() і
і ![]() - так, оскільки однакові показники коренів та підкореневі вирази б)
- так, оскільки однакові показники коренів та підкореневі вирази б) ![]() і
і ![]() - ні, оскільки різні показники коренів.
- ні, оскільки різні показники коренів.
в) ![]() і
і ![]() - ні, оскільки різні підкореневі вирази.
- ні, оскільки різні підкореневі вирази.
Приклад 4. Довести подібність: 1) ![]() і
і ![]()
Розв’язок: ![]()
![]()
Маємо подібні радикали, показники кореніврівні і підкореневі вирази одинакові.
Дії з радикалами.
Додавання і віднімання. Додавання і віднімання радикалів виконують так само, як і додавання і віднімання раціональних одночленів. Щоб додати(або відняти) радикали, їх з’єднують знаком плюс(чи мінус), виявляють подібні члени, якщо вони є, а потім їх додають.
Приклади. Виконати дії:
Розв’язок:![]()
![]()
Розв’язок:![]()
![]() .
.
Множення.
Щоб перемножити декілька радикалів однакового степеня, потрібно перемножити підкореневі вирази і добути корінь з добутку того ж степеня.
Якщо перемножуються радикали з різними показниками, то їх потрібно спочатку звести до одного показника. Якщо перед радикалами є коефіцієнти, то їх перемножають.
Приклад 1. Виконати множення:
а) ![]() .
.
Розв’язок: ![]()
б) ![]() .
.
Розв’язок:![]()
![]()
в) ![]()
Розв’язок:![]()
Приклад 2. Перемножити радикали з різними показниками:
а) ![]()
Розв’язок: ![]()
б) ![]()
Розв’язок: для степенів коренів 2,3,4,6 знаходимо найменше спільне кратне – 12 і переходимо до кореня 12 степеня:
![]()
![]() .
.
Ділення. Щоб поділити радикали з однаковими показниками, потрібно розділити їх підкореневі вирази і з частки добути корінь того ж степеня.
Щоб розділити радикали з різними показниками, їх потрібно привести спочатку до одного показника. Якщо є коефіцієнт, то їх ділять.
Приклад 1. Виконати ділення:
а) 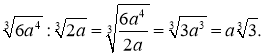
б)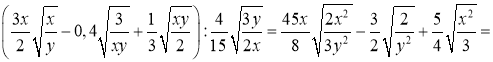
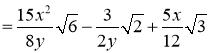 .
.
в) ![]()
![]()
г) ![]() .
.
Приклад 2. Виконати ділення, використовуючи формули скороченого множення:
![]()
![]()
Піднесення до степеня.
Щоб піднести радикал до степеня, потрібно піднести до цього степеня підкореневий вираз, залишивши той же показник радикала:
![]() .
.
Приклади. 1. ![]()
![]()
2.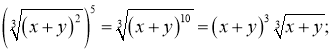
3.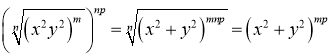 .
.
Алгебраїчні суми радикалів можна підносити до степеня, користуючись формулами скороченого множення.
Приклади. 1. ![]()
2.![]()
![]()
Добування кореня.
Щоб добути корінь з кореня, потрібно перемножити показники коренів: ![]()
Приклади: ![]()
![]()
Квадратний корінь із двочлена виду A±![]() .
.
При перетворенні виразів, такого виду:
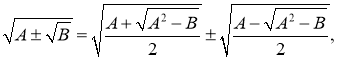
![]()
де ![]() і
і ![]() , знаки в правій і лівій частині одночасно беруться чи верхні чи нижні(відповідно). Ця формула називається формулою складного радикала.
, знаки в правій і лівій частині одночасно беруться чи верхні чи нижні(відповідно). Ця формула називається формулою складного радикала.
Приклади:
1. 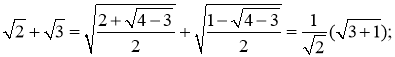
2.
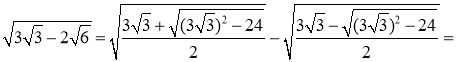
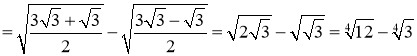 .
.


про публікацію авторської розробки
Додати розробку
