Конспект уроку на закріплення знань з теми "Види сполук. Комбінаторні задачі."

УРОК

Тема уроку. Розв'язування комбінаторних  задач.

Мета уроку: вчити розрізняти види сполук і знаходити їх число за  

відповідними формулами, розв'язувати нескладні комбінаторні задачі.

І. Перевірка домашнього завдання.

1. Перевірити правильність виконання домашніх вправ за допомогою слайдів, зроблених до початку уроку.

Завдання.

1) Із Києва до Сімферополя можна дістатися або поїздом, або автобусом, або літаком, а з Сімферополя до Ялти - або автобусом, або тролейбусом. Скільки існує різних способів дістатися до Ялти з Києва через Сімферополь?

А)  2+3;     Б) 2∙3 ;  В) 2³ ;   Г) 3²;      Д)  (2+3)! .

2). За умовою попередньої задачі знайдіть кількість варіантів здійснення подорожі за маршрутом Київ - Сімферополь - Ялта - Сімферополь - Київ, якщо зворотний шлях провести в поїзді.

А) 6;      Б) 12;     В) 18;   Г) 24;   Д) 36 .

3). Скільки тризначних чисел можна утворити, використовуючи три картки з цифрами: 1, 5, 5?

А)одне;               Б) два;  В) три;                 Г) чотири;          Д) більше чотирьох .

4). Скільки трикутників можна скласти, обираючи три з чотирьох відрізків, довжини яких дорівнюють 1 см, 1 см, 2 см і 3 см?

А)  жодного;     Б)  один;             В) два ;                Г) три;  Д) більше трьох.

5.. Телеведучий має надати слово чотирьом особам: журналісту А, експерту Б, чиновнику В і депутату Г. Скільки існує різних способів виступу гостей студії, якщо чиновник В категорично відмовляється виступати раніше, ніж депутат Г?

А)  24;   Б)  18;   В) 12;   Г) 6;         Д)  3.

II. Сприймання і усвідомлення відомостей про комбінаторні задачі, правил суми і добутку.

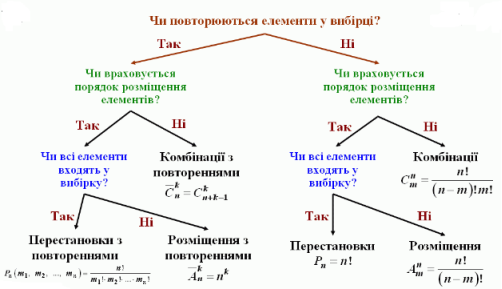
Комбінації, розміщення і перестановки разом називаються сполуками. Розділ математики, в якому розглядаються властивості сполук, називають комбінаторикою, а задачі цього розділу — комбінаторними задачами.

Перестановки відрізняються одна від одної порядком розташування елементів.

Розміщення відрізняються або вибором елементів, або порядком їх розташування.

Комбінації відрізняються тільки вибором елементів (порядок розміщення елементів не враховується).

Таблиця 1

Математичний диктант  ( відповіді підготовлені до початку уроку)

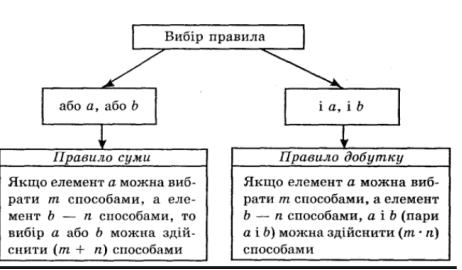
Комбінаторні задачі бувають різних видів. Але більшість із них розв'язують за допомогою двох основних правил: правила суми і правила добутку (таблиця 2).

Таблиця 2

Виконання вправ.

1.Є дві паралельні прямі. На першій з них вибрано n різних точок, а на другій - k різних точок. Скільки існує трапецій з вершинами в цих точках?

А) C⁴_n+k;               Б) A⁴_n+k;               В) C²_n∙A²_k;           Г) A²_n∙A²_k;           Д) C²_n∙C²_k.

2. На випускному вечорі присутні n дівчат і m хлопців. Скількома способами можна утворити з них k пар для виконан­ня вальсу (k < m < n)

А) C^k_n∙C^k_m;          Б) C^k_n+C^k_m;    В)  A^k_n∙A^k_m;             Г) A^k_n+A^k_m;   Д) C^k_n∙A^k_m.

3.Збори з 30 осіб обирають голову, секретаря та трьох членів редакційної комісії. Скількома способами це можна зробити?

Відповідь: .

4.Із 10 троянд і 8 жоржин треба скласти букет так, щоб в ньому були 2 троянди і 3 жоржини. Скількома способами можна скласти букет?

Відповідь:· = 2520

5.Скільки різних прямих можна провести через 5 точок площини, з яких ніякі три не лежать на одній прямій?

Відповідь:=10.

6.Яка найбільша кількість різних  трицифрових чисел, які можна складати з цифр 1, 2, 3, 4, 5, 6, якщо цифри в числі можуть повторюватися?

 А) С⁶₃;  Б) (6!):(1!∙2!∙3!) = 60;  В) 6∙(2∙3∙1);   Г) 6∙5∙4;   Д) 216 = 6∙6∙6.

7.Завуч має скласти розклад для 11-го класу на понеділок, маючи для цього сім різних уроків. Скільки існує різних варіантів такого розкладу?

А) 7;   Б) 7∙7;  В) 7∙7∙7∙7∙7∙7∙7;  Г)7! = 1∙2∙3∙4∙5∙6∙7;   Д)77.

8.Скільки існує різних способів складання трикольорового прапора з вертикальними смугами, якщо є тканина п'яти різних кольорів?           

А) 10;    Б)  15;   В)  30;   Г) 60;  Д) 120 .

9. 7 книг різних авторів і трьохтомник одного автора розташовані на книжковій полиці. Скількома способами можна розставити ці 10 книжок на полиці так, щоб книги автора трьохтомника стояли поруч?

Відповідь: P₃ P₈

III. Підведення підсумків уроку.

IV. Домашнє завдання.

Закріпити теоретичні поняття теми.

1.Контрольні запитання

1. Дайте визначення комбінаторики.

2. Поясніть, що являють собою задачі на перелічення.

3.Поясніть, що являють собою задачі про вибір.

4. Що вивчає комбінаторика?

5. Поясніть появу «задачі про кроликів». Як її розв’язував Леонардо Пізанський (Фібоначчі)?

6. Сформулюйте правило суми для комбінаторних задач. Поясніть на прикладі використання правила суми.

7. Сформулюйте правило добутку для комбінаторних задач. Яка формула використовується у правилі добутку?

8. Надайте визначення перестановки k-елементів.

9. Надайте визначення розміщення з n по k елементів.

10. Що являє собою розміщення з повтореннями з n по k елементів? За якою формулою обчислюється кількість k-розміщень з повтореннями з n по k елементів?

2. Контрольний тест.

1.У гральній колоді 36 карт. Яка ймовірність того, що взята навмання карта є тузом?

2. Із цифр 5, 6, 7, 8, 9 складено всі можливі п’ятицифрові числа без повторення цифр. Скільки серед цих чисел непарних?

3. 28 кісток доміно навмання виймають одну. Яка ймовірність того, що: 1) сума цифр на ній більша ніж 9; 2) обидві цифри на ній непарні?

4. В урні міститься 12 кульок: чотири білі і вісім чорних. Навмання виймають три кульки. Яка ймовірність, що серед вийнятих кульок усі три – білі?

5. З літер слова «професор» послідовно вибирають чотири літери. Знайдіть імовірність того, що вибрані літери в порядку їх вибору утворять слово «прес».

6. У гральній колоді 36 карт. Яка ймовірність того, що взята навмання карта є королем?

7. Із цифр 1, 2, 3, 4, 5 складено всі можливі п’ятицифрові числа без повторення цифр. Скільки серед цих чисел непарних?