Конспект уроку "Найпростіші тригонометричні рівняння"
Тема уроку: Найпростіші тригонометричні рівняння та їх розв’язання
Тип уроку: комбінований
Мета уроку:
Дидактична –сформувати поняття найпростіших тригонометричних рівнянь; домогтися засвоєння формули для розв’язання рівняння
; сформувати вміння розв’язувати найпростіші тригонометричні рівняння;
Розвивальна – розвивати пам'ять і мислення; розвивати цікавість до математики, прагнення краще вчити предмет; здатність до творчого застосування знань і вдосконалення умінь;
Виховна – виховувати наполегливість і відповідальність, допитливість, уважність, натхнення, любов до навчання та вміння працювати разом, виховувати акуратність при побудові графіків функцій.
Формування компетентностей:
Соціальна компетентність: самостійне розв’язання завдань різними способами і вибір раціональніших, самооцінка і взаємооцінка.
Комунікативна компетентність: стимулювання умінь учнів, коментування розв’язаних завдань, взаємоперевірка вислову власної точки зору.
Інформаційна компетентність: використання додаткової інформації; використання таблиць, схем, опорних конспектів.
Полікультурна компетентність: зв'язок з іншими предметами, життєвими ситуаціями, моделювання.
Продуктивна творча діяльність: використання творчих завдань, складання завдань, питань, алгоритмів.
Тип уроку: комбінований (застосування інтерактивних технологій).
Матеріально-технічне забезпечення та дидактичні засоби: підручник, презентація, роздатковий матеріал
\ХІД УРОКУ:
Організаційна частина:
Привітання, перевірка присутності учнів і готовності класу до уроку.
Актуалізація опорних знань учнів:
Кожен учень отримує інтелект-картку для перевірки готовності до уроку.
Після роботи з карткою виконується взаємоперевірка за дошкою.
Мотивація навчальної діяльності:
Рівняння – це не просто рівність
З одною змінною чи кількома.
Рівняння- це думок активність.
Це інтелекту боротьба
Розв’язування будь-якого тригонометричного рівняння зводиться до розв’язування найпростіших рівнянь, тому дуже важливо мати навички розв’язування найпростіших тригонометричних рівнянь
Повідомлення теми і мети уроку.
Щоб успішно засвоювати нові знання, формувати нові вміння та навички, треба домогтися ґрунтовного засвоєння попередніх. Його проводимо з використанням таких прийомів.
- Фронтальне виконання практичних завдань:
Найпростіші тригонометричні рівняння та їх розв’язання.
- Встановити відповідність.
-
-
-
-
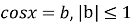Г.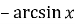 
-
-
-
-
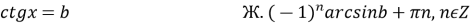
Відповідь: ГЖДАВБЕЄ
2. Робота з моделлю тригонометричного кола
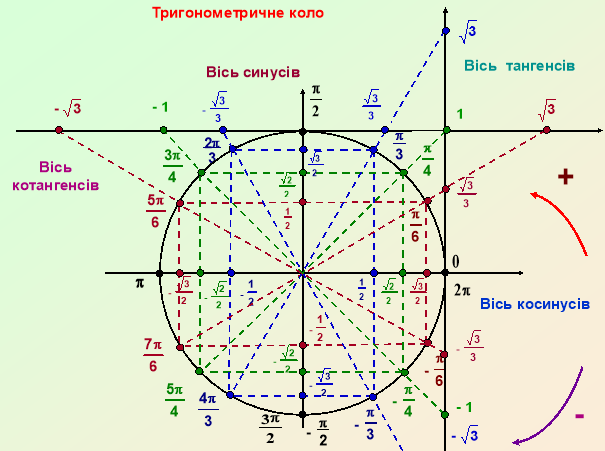
- дати означення синуса, косинуса, тангенса, котангенса кута;
- назвати межі координатних чвертей;
- назвати знаки тригонометричних функцій в кожній чверті;
Повідомлення нових знань за планом
Задача. Сторони трикутника дорівнюють 8см і 15см. Знайдіть кут між ними, якщо площа трикутника 30см2. [1]
Розв’язання.
, де а і в – сторони трикутника, α – кут між ними.
Маємо рівняння:
Невідоме входить під знак синусу, тригонометричної функції. Такі рівняння називаються тригонометричними. Наша задача – навчитися їх розв’язувати. На розв’язування таких рівнянь програмою для гуманітарних класів відводиться небагато часу. Але розв’язання тригонометричних рівнянь є невід’ємною складовою багатьох процесів, які відбуваються навколо нас. Навчитися розв’язувати найпростіші – обов’язково! для кожного із вас. Головне – це вивчити формули, за допомогою яких знаходимо корені найпростіших тригонометричних рівнянь і навчитися застосовувати їх до розв’язування відповідних рівнянь
|
|
Рівняння |
Розв'язання |
|
1 |
cos x = a |
|a| ≤ 1, x = ± arccos a + 2πn, n є Z |
|
2 |
cos x = 0 |
x = + πn, n є Z |
|
3 |
cos x = 1 |
x = 2πn, n є Z |
|
4 |
cos x = - 1 |
x = π + 2πn, n є Z |
|
5 |
cos x = - a |
|a| ≤ 1, x = ±(π-arccos a)+ 2πn, n є Z |
Розв’язування будь якого тригонометричного рівняння зводиться до розв’язування найпростішого з тригонометричних рівнянь
Головне, щоб учень самостійно оформив свій опорний конспект, щоб сам виділив поняття, зв'язки між ними і зобразив їх за допомогою лише йому зрозумілих малюнків, креслень, символів та умовних позначень. Опорне конспектування за допомогою скорочень, позначень, символів, стрілок, з'єднань і т. д. є дуже ощадною формою кодування думок, замінює нераціональне «лінійне» конспектування, тобто дослівний запис інформації.
|
sin x = a |
cos x = a |
tg x = a |
ctg x = a |
|
Дослідження |
|||
|
х – будь яке |
х – будь яке |
|
|
|
1) якщо |
1) якщо |
При будь якому а рівняння має корені, які
знаходимо за формулою: |
При будь якому а рівняння має корені, які
знаходимо за формулою: |
|
2) якщо |
2) якщо |
||
|
Окремі випадки |
|||
|
а = 0 |
а = 0 |
а = 0 |
а = 0 |
|
sin x = 0
|
cos x = 0
|
tg x = 0
|
ctg x = 0
|
|
а =1 |
а =1 |
а =1 |
а =1 |
|
sin x = 1
|
cos x = 1
|
tg x = 1
|
ctg x = 1
|
|
а = -1 |
а = -1 |
а = -1 |
а = -1 |
|
sin x = -1
|
cos x = -1
|
tg x = -1
|
ctg x = -1
|
Таблиця 1
При розв’язуванні найпростіших тригонометричних рівнянь необхідно знаходити аркуси відповідних чисел.
|
Аркуси |
||||
|
arcsin a – кут з проміжку |
arccos a – кут з проміжку |
arctg a – кут з проміжку
|
arcctg a – кут з проміжку |
|
|
Знаходження аркусів відємних чисел |
||||
|
arcsin ( - a) = - arcsin a |
arccos ( - a) = π - arccos a |
arctg ( - a) = - arctg a |
arcctg ( - a) = π - arcctg a |
|
Таблиця 2
Таблиця значень тригонометричних функцій деяких кутів
|
|
