Конспект уроку "Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу"
Урок №7. Тема: Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу.
Формування компетентностей:
предметна компетентність:
- закріплення учнями змісту: властивостей числових нерівностей і теорем про почленне додавання та множення нерівностей;
- розвивати уміння відтворювати зміст вивчених понять; застосовувати їх для розв'язування вправ: на порівняння виразів, на доведення нерівностей, а також на оцінювання значень виразів;
ключові компетентності:
- спілкування державною мовою – уміння доречно та коректно вживати в
мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;
- математична компетентність – уміння оперувати числовою інформацією;
- уміння вчитися впродовж життя – уміння оцінювати результати своєї
навчальної діяльності.
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання та наочність: підручник з алгебри за 9 клас, автори: Мерзляк, Полонський, Якір, 2017 р.
Хід уроку
I. Організаційний момент.
- Налаштовування на роботу.
- Перевірка домашнього завдання:
(§1 п.2 № 2.8, 2.17)
№2.8. Відомо, що ![]() . Порівняйте з нулем значення виразу:
. Порівняйте з нулем значення виразу:
![]()
![]()
Отже, ![]()
![]()
![]()
Отже, ![]()
![]()
![]()
Отже, ![]()
![]()
![]()
![]()
Тоді, ![]()
![]()
![]()
![]()
Тоді, ![]()
Отже, ![]() .
.
-
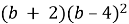 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Тоді, ![]() і
і ![]() .
.
Отже, ![]() .
.
![]() тоді
тоді ![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]() ;
;
Тоді ![]() .
.
Отже, ![]() .
.
№2.17. Дано: ![]() . Доведіть, що:
. Доведіть, що:
-
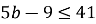 ;
;
![]() ;
;
![]() ;
;
Отже, ![]() .
.
-
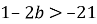 ;
;
![]() ;
;
![]() ;
;
Отже, ![]() , тоді
, тоді ![]() .
.
II. Актуалізація опорних знань.
Фронтальне опитування
-
Яке із чисел —
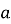 або
або 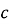 — більше, якщо відомо, що
— більше, якщо відомо, що 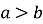 і
і 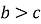 ?
?
- Сформулюйте теорему про додавання до обох частин нерівності одного й того самого числа.
- Сформулюйте наслідок із теореми про додавання до обох частин нерівності одного й того самого числа.
- Сформулюйте теорему про множення обох частин нерівності на одне й те саме число.
- Сформулюйте наслідок із теореми про множення обох частин нерівності на одне й те саме число.
III. Вивчення нового матеріалу
Мотивація навчальної діяльності учнів
Імовірно, що при перевірці виконання тестових завдань (див. вище) учні зроблять кілька типових помилок. У цьому разі мета уроку (закріплення знань властивостей числових нерівностей та відпрацювання навичок їх застосування) формулюється з усвідомлення учнями необхідності виправлення помилок та проведення роботи з профілактики подібних помилок надалі. Якщо ж більшість учнів впораються із запропонованими завданнями на «відмінно», мотивація до роботи може бути створена вчителем за допомогою завдання підвищеної складності або завдання такого типу, яке не було розглянуто на попередньому уроці (створюємо проблему). У будь-якому разі вчитель має налаштувати учнів на необхідність формування більш стійких знань властивостей числових нерівностей та їхніх наслідків, а також на роботу з вироблення навичок роботи з цими властивостями.
План вивчення нового матеріалу
- Властивість про почленне додавання числових нерівностей (з доведенням).
- Властивість про почленне множення числових нерівностей (з доведенням).
- Наслідок. Властивість про почленне множення числових нерівностей (з доведенням).
Опорний конспект
Теорема 3.1 (про почленне додавання нерівностей).
Якщо ![]() і
і ![]() , то
, то ![]()
Доведення. Розглянемо різницю ![]() Маємо:
Маємо:
![]()
Оскільки ![]() і
і ![]() , то різниці
, то різниці ![]() і
і ![]() є додатними числами. Отже, різниця, що розглядається, є додатною, тобто
є додатними числами. Отже, різниця, що розглядається, є додатною, тобто ![]()
Теорема 3.2 (про почленне множення нерівностей).
Якщо ![]() ,
, ![]() і
і ![]() — додатні числа, то ac>bd.
— додатні числа, то ac>bd.
Доведення. Розглянемо різницю ![]() Маємо:
Маємо:
![]()
За умовою ![]() . Отже, різниця, що розглядається, є додатною. Із цього випливає, що
. Отже, різниця, що розглядається, є додатною. Із цього випливає, що ![]()
Наслідок. Якщо ![]() і
і ![]() — додатні числа, то
— додатні числа, то ![]() , де
, де ![]() — натуральне число.
— натуральне число.
Доведення. Запишемо n правильних нерівностей ![]() :
:
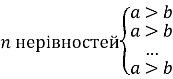
Оскільки ![]() і
і ![]() — додатні числа, то можемо перемножити почленно n записаних нерівностей. Отримаємо:
— додатні числа, то можемо перемножити почленно n записаних нерівностей. Отримаємо: ![]() .
.
IV. Засвоєння нових знань і способів дій
№ 3.1. Запишіть нерівність, яку отримаємо, якщо:
1) додамо почленно нерівності ![]() і
і ![]() ;
;
2) перемножимо почленно нерівності ![]()
3) перемножимо почленно нерівності ![]() .
.
№ 3.6. Дано: ![]() і
і ![]() . Оцініть значення виразу:
. Оцініть значення виразу:
1) ![]() ; 2)
; 2) ![]() 3)
3) ![]()
№ 3.9. Оцініть середнє арифметичне значень ![]() і
і ![]() якщо відомо, що
якщо відомо, що
![]()
№ 3.14. Відомо, що ![]() і
і ![]() . Доведіть, що
. Доведіть, що ![]() .
.
№ 3.19. Доведіть, що периметр чотирикутника більший за суму його діагоналей.
V. Підбиття підсумків уроку, рефлексія
Визначте й обґрунтуйте, чи є правильним твердження:
- якщо а – b = т2 + 1, то а > b;
- якщо а < b, то а + 3 < b + 3;
- якщо 1 < 3х, то 3х < 1;
- якщо х < 2, у < 3, то х + у < 5, ху < 6.
VI. Домашнє завдання
(§1 п.3 № 3.11, 3.17)


про публікацію авторської розробки
Додати розробку
