Контрольна робота .

Арифметична та геометрична прогресії.                                               9 клас

Варіант 1

1.  Яка з поданих послідовностей є арифметичною прогресією?
        а) 1; 2; 4; 8;  б) 8; 10; 13; 17;   в) 2; 4; 6; 8;   г) -8; 8; -8; 8.

2. Якщо  b₈= –3,4; b₉ = 6,8, то знаменник геометричної прогресії (b_п) дорівнює... 

                а) 10,2;       б)3,4;      в)-2;       г) ;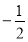 

3. Різниця арифметичної прогресії 22; 18; 14; 10;... дорівнює...

                    а) 4;         б)-4;   в) 40;        г) 6; 

4. Четвертий член геометричної прогресії 0,1; 0,3; 0,9;... дорівнює...              

                а) 0,27;     б)2,7;   в) 1,2;        г)2,4; 

5. Знайдіть п’ятий член  і суму  4 перших членів геометричної прогресії (b_n) b₁=5, q=2.

6. Чому дорівнює сума перших 10 членів арифметичної прогресії  (a_n), якщо a₅= -0,8, a₁₁= -2.

7. Знайдіть перший член геометричної прогресії, якщо  різниця третього і  першого членів дорівнює 6, а другого і першого  дорівнює  - 2.

Контрольна робота .

Арифметична та геометрична прогресії.                                               9 клас

Варіант 2

1.  Яка з наведених послідовностей є геометричною прогресією?
а) 2; 6; 18; 36; б) 80; 40; 20; 5;  в) 4; 8; 16; 32;  г) 2; -10; 50; 250.

2. Знайдіть різницю арифметичної прогресії (a_n), якщо а₁ = 4,5; а₂ = 4,2.
              а) 0,3;            б) -0,3;            в) 3;            г) -3.

3. Знайдіть перший член геометричної прогресії, якщо її другий член b₂= -20, а знаменник q= -5.
а) 4;                    б) -4;                в) -100;                 г) 100.

4. Знайдіть сьомий член арифметичної прогресії, перший член якої дорівнює  8, а різниця дорівнює 0,5.
а) 11;             б) 10;               в) 10,5;             г) 9,5.

5. Знайдіть четвертий член  і суму  4 перших членів геометричної прогресії (b_n) b₁=3, q=3.

6. Чому дорівнює сума перших 10 членів арифметичної прогресії  (a_n), якщо a₄= -6, a₇= 2,4.

7. Знайдіть перший член геометричної прогресії, якщо  різниця третього і  першого членів дорівнює 6, а другого і першого  дорівнює  - 2.