Конспект уроку, презентація з вкрапленнями сюжетів художніх фільмів до теми "Графічний спосіб розв’язування систем рівнянь другого степеня з двома змінними."
Тема. Графічний спосіб розв’язування систем рівнянь другого степеня з двома змінними.
Мета.
- формувати вміння й навички розв'язання систем рівнянь із двома змінними другого степеня графічним способом
- розвивати прийоми розумової діяльності (узагальнення, аналіз, синтез, порівняння);
- виховувати здатність логічно та аналітично мислити, увагу й акуратність під час виконання графічних робіт.
Тип уроку: Урок засвоєння нових знань і навичок.
Обладнання: презентація, конспект
ХІД УРОКУ
І. Перевірка домашнього завдання
Учитель з'ясовує, які завдання учні не виконали
2. Організаційний момент.
"Те, що я чую, я забуваю.
Те, що я бачу і чую, я трохи пам’ятаю.
Те, що я чую, бачу і обговорюю,
я починаю розуміти.
Коли я чую, бачу, обговорюю й роблю,
я набуваю знань та навичок.
Коли я передаю знання іншим,
я стаю майстром.”
ІІ. Актуалізація опорних знань.


Графіком якої функції є коло ? пряма? парабола? гіпербола?
- 2х – 3у + 4 = 0;
- (х – 3)² + (у +2)² = 9;
- у = х² - 2х - 3;
- ху = 4
- у = 2х – 1;
- у = 3;
- у = - х² + 4х - 3;
- х² + у² = 25;
- у = - 4.
![]()
II. Повідомлення теми уроку
III. Мотивація навчальної діяльності

Учитель. Теорія систем рівнянь має багатовікову історію. З такими задачами ми зустрічаємося і в житті. Багато задач пов'язані з визначенням залежностей однієї величини від кількох факторів. Для математичного опису такої залежності використовують поняття функції кількох змінних. З такими залежностями ми зустрічаємося і в астрономії.

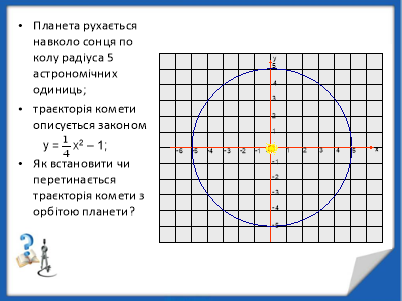
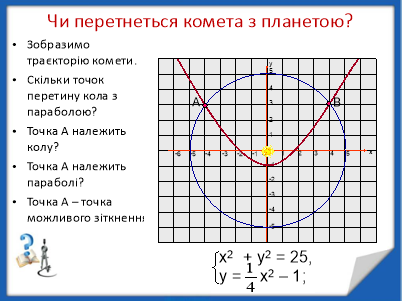
ІV. Пояснення нового матеріалу
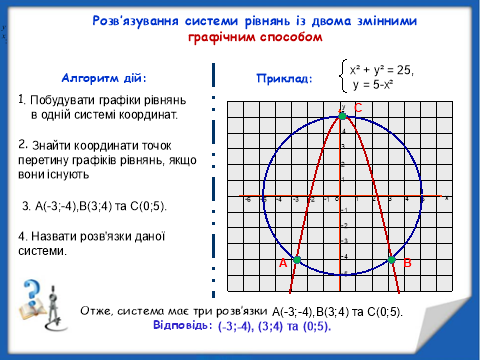
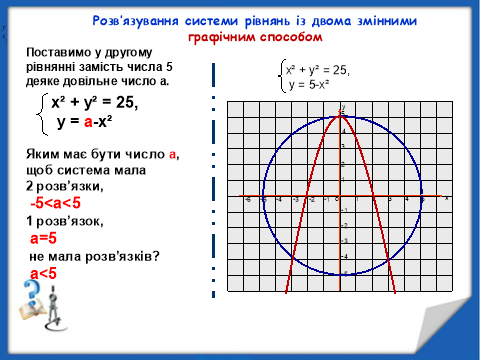
- Закріплення та усвідомлення знань учнів.
Продовжимо астрономічну тему



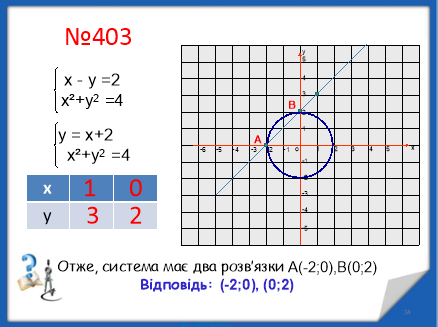

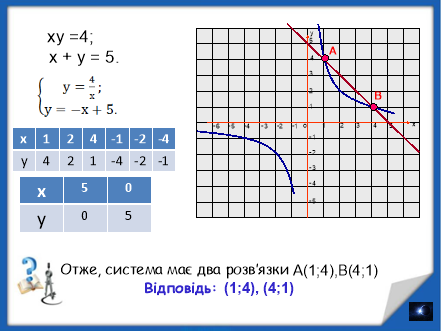
6. Індивідуальні завдания по карткам.
Клас розділено на 6 груп по 4-6 учнів в кожній. Кожна група отримує картку з завданням /Додаток 1/. Завдання обговорюються, розподіляються між учнями: два учні виконують роботу в зошиті, двоє учнів розв’язують по одній системі. Отримавши відповідь, вони звіряють розв’язки. Учитель перевіряє правильність розв’язання.

- Підсумок уроку
VIII. Домашнє завдання №404, 408,419
Картка № 1
-
З’ясувати кількість розв’язків системи
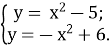
1) 1 розв’язок, 2) 2 розв’язки, 3) 3 розв’язки, 4) розв’язків немає
-
Розв’язати систему рівнянь :
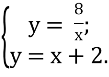
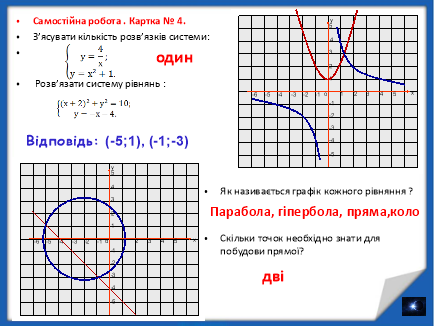
- Як називається графік кожного рівняння ?
- Скільки точок необхідно знати для побудови прямої?
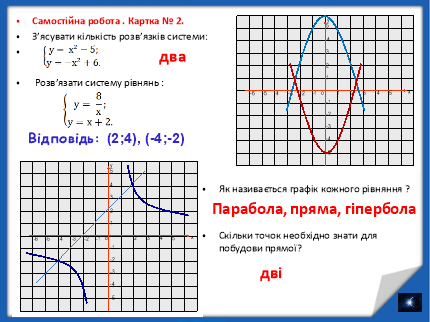
Картка № 2
-
З’ясувати кількість розв’язків системи:
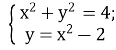
1) 1 розв’язок, 2) 2 розв’язки, 3) 3 розв’язки, 4) розв’язків немає
-
Розв’язати систему рівнянь:
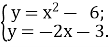
- Як називається графік кожного рівняння ?
- Скільки точок необхідно знати для побудови прямої?
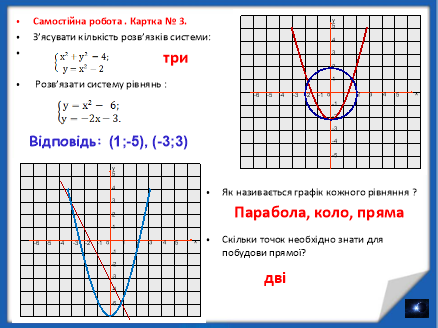
Картка № 3
-
З’ясувати кількість розв’язків системи:
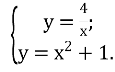

1) 1 розв’язок, 2) 2 розв’язки, 3) 3 розв’язки, 4) розв’язків немає
-
Розв’язати систему рівнянь:
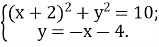
- Як називається графік кожного рівняння ?
- Скільки точок необхідно знати для побудови прямої?
|
Бланк відповідей Прізвище __________________________ Варіант№________________ |
Бланк відповідей Прізвище __________________________ Варіант№________________ |
|||
|
Завдання № 1 |
|
Завдання № 1 |
|
|
|
Завдання № 2 |
|
Завдання № 2 |
|
|
|
Завдання № 3 |
|
Завдання № 3 |
|
|
|
Завдання № 4 |
|
Завдання № 4 |
|
|
|
Бланк відповідей Прізвище __________________________ Варіант№________________ |
Бланк відповідей Прізвище __________________________ Варіант№________________ |
|||
|
Завдання № 1 |
|
Завдання № 1 |
|
|
|
Завдання № 2 |
|
Завдання № 2 |
|
|
|
Завдання № 3 |
|
Завдання № 3 |
|
|
|
Завдання № 4 |
|
Завдання № 4 |
|
|
|
Бланк відповідей Прізвище __________________________ Варіант№________________ |
Бланк відповідей Прізвище __________________________ Варіант№________________ |
|||
|
Завдання № 1 |
|
Завдання № 1 |
|
|
|
Завдання № 2 |
|
Завдання № 2 |
|
|
|
Завдання № 3 |
|
Завдання № 3 |
|
|
|
Завдання № 4 |
|
Завдання № 4 |
|
|
|
Бланк відповідей Прізвище __________________________ Варіант№________________ |
Бланк відповідей Прізвище __________________________ Варіант№________________ |
|||
|
Завдання № 1 |
|
Завдання № 1 |
|
|
|
Завдання № 2 |
|
Завдання № 2 |
|
|
|
Завдання № 3 |
|
Завдання № 3 |
|
|
|
Завдання № 4 |
|
Завдання № 4 |
|
|
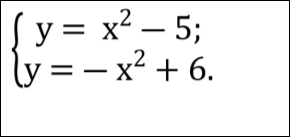
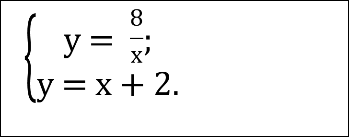
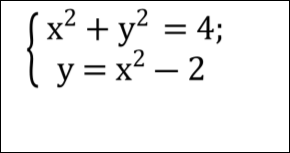
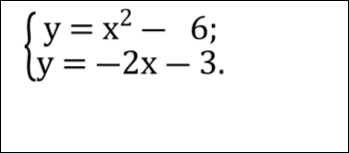
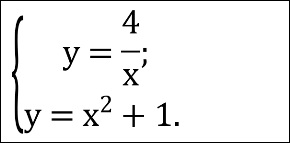
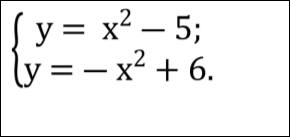
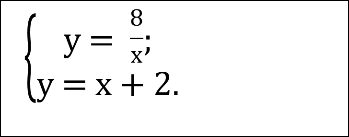
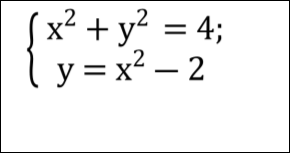
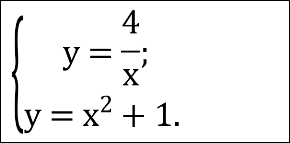
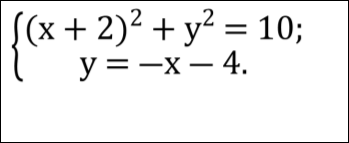


про публікацію авторської розробки
Додати розробку




































































































