Підготувала і провела

                                                                        вчитель математики

                                                                        Ховдій В.О.

 

Тема: Теорема Піфагора. Розв’язування задач.

Мета:

• формування предметних компетентностей: удосконалити вміння застосовувати теорему Піфагора до розв’язування задач, у тому числі прикладного характеру; сформувати вміння використовувати піфагорові трійки; формувати вміння «бачити» прямокутні трикутники, які є частинами інших геометричних фігур.
•                   формування ключових компетентностей: формувати вміння оперувати геометричними об’єктами на площині; сприяти самовихованню допитливості, усвідомленню власних освітніх потреб, цінності нових знань і вмінь; формувати вміння абстрактно мислити, виділяти головне у досліджуваному матеріалі, генерувати нові ідеї; сприяти вихованню толерантності, ініціативності, уважності; сприяти усвідомленню значення математики для повноцінного життя в сучасному суспільстві; удосконалювати здатність безпечного та етичного використання засобів інформаційно-комунікаційної компетентності у навчанні.

Тип уроку: урок формування та вдосконалення компетентностей

Обладнання: інтернет-ресурси, QR-коди, презентація, відео.

Хід уроку

1. Організаційний етап.

Доброго дня, любі діти.

Давайте глянемо навкруги. Чи бачимо ми щось, що пов’язує нас з геометрією?

Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання. І нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір.

Я сподіваюсь на нашу співпрацю, свідоме засвоєння матеріалу уроку.

Давайте згадаємо, на попередньому  уроці ми вивчили: теорему нареченої, теорему німфи, теорему метелика, теорему 100 биків, «втечу убогих» і «міст ослів».

Ви мені скажете: « Ні. Ми вивчили одну теорему – теорему Піфагора».

Цілком вірно: ці назви стосуються всього однієї теореми. І як ви здогадалися – ця теорема носить назву – теорема Піфагора.

ІІ. Перевірка домашнього завдання.

Давайте перевіримо як ви засвоїли пройдений матеріал. Для цього виконаємо тест в телефонах(посилання в нашій групі ).

ІІІ. Повідомлення теми, мети уроку.

На сьогоднішньому уроці ми продовжимо працювати над застосуванням теореми Піфагора.

Ми перевіримо, наскільки добре  вивчили та зрозуміли цю визначну теорему, а також спробуємо здобути навички використання цієї теореми для розв’язування задач; познайомимося з людиною, ім'я якої носить дана теорема; спробуємо запам’ятати найпоширеніші піфагорові трійки та використати їх в задачах, що може стати вам у нагоді при складанні ЗНО.

Тому записуємо тему сьогоднішнього уроку.

А гаслом цього уроку я обрала слова чоловіка, якого довгий час не допускали до участі до змагань з боротьби через його малу масу, та який завдяки своїй наполегливості зумів стати врешті-решт стати олімпійським чемпіоном:

Тимчасова невдача краще, ніж тимчасова удача.

    Піфагор

 ІV. Актуалізація опорних знань                                                                                                                                                                

   Хто є автором цих слів? Дати відповідь на це запитання допоможе нам інтерактивна вправа «Вірю – не вірю».

Перед вами з’являються повідомлення, якщо відповідь правильна, ми виписуємо літеру під знаком «+», якщо неправильна, під знаком «-».

Запитання.	+	-
Сторони, які утворюють прямий кут у прямокутному трикутнику називаються катетами.	А	У
Гіпотенуза – це найменша сторона трикутника.	К	П
Катет, який лежить проти кута 300 у два рази більший за гіпотенузу.	Е	О
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.	І	Я
Гіпотенуза – сторона прямокутного трикутника, яка лежить проти гострого кута.	К	Ф
Трикутник зі сторонами 6 см, 8 см і 10 см – прямокутний.	Р	Н
Якщо катет, який лежить проти кута 300 , дорівнює 6 см, то гіпотенуза може дорівнювати 10 см.	Б	Г

 

Розгадаємо анаграму. З літер, які ви виписали, складемо прізвище автора слів, які ми взяли гаслом нашого сьогоднішнього уроку. 

Так ці слова належать Піфагору.

Отож, удачі нам усім, і хай вона буде не тимчасовою!

V. Вивчення нового матеріалу.

• А що ви знаєте про Піфагора, крім того, що теорема, яку ми вивчали на минулому уроці, носить його ім’я? Давайте познайомимося з цим вченим.

1. Відео про Піфагора, створено учням класу.

Повідомлення вчителя.

Ми добре знаємо сторони Єгипетського трикутника 3, 4, 5.

А чи є ще такі трійки чисел? Відповідь на це запитання знайшли мудреці Стародавнього Вавилону.  Знав це і Піфагор. Один із шляхів вирішення рівняння х² + у² = z² в цілих числах виявився доволі простим. Запишемо підряд квадрати натуральних чисел, відділивши їх одне від одного комами. Під кожною комою запишемо різницю між послідовними квадратами.

 

 

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196

 3, 5, 7,  9,  11, 13, 15, 17, 19,   21,   23,   25,   27

                (3,4,5)                                                             (5, 12, 13)

Це Піфагорові трійки.

Ще одна трійка відома ще в Стародавньому Єгипті – (7, 24, 25).

Ці формули – правила були відомі вже дві з половиною тисячі років тому. А використовувати цей спосіб знаходження Піфагорових трійок є дуже простим і цікавим.

VІ. Розв’язування задач.

1. «Впіймай помилку»

На дошці записані задачі з розв’язаннями, які містять помилки. Знайти і виправити помилки.

1.  

2.  

 

 

3.  

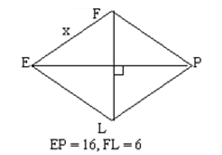
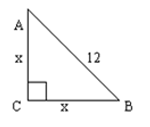
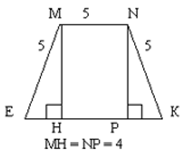Знайти ЕК.

 

 

 

 

2. «Задачі за готовими малюнками».

Інтерактивна вправа https://learningapps.org/display?v=pbcoejk5c21

Колективне виконання:

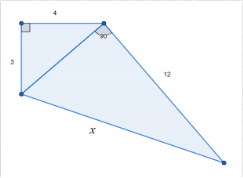
Робота в групах:

Група 1:

 

 

 

 

 

 

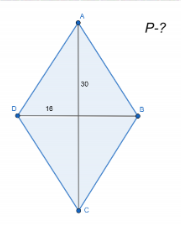
Група 2:

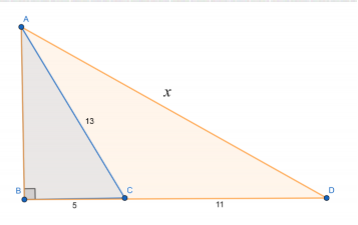
Група 3:

 

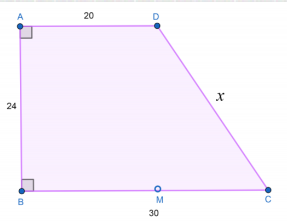
3. Розв’язування задач практичного змісту.

Колективне виконання:

   Завдання індійського математика  XII століття Бхаскары

          

                            «На березі річки росла самотня                   

                            тополя.

                             Раптом налетівші вітри зламали                

                              Її  стовбур.

                              Бідна тополя впала, утворивши 

                              кут між стовбуром і поверхнею            

                              води річки.

                              Запам'ятай тепер, що в цьому

                                                                             місці річка

                              У чотири лише фута була шириною.

                               Верхівка зламалася, залишивши всього

                               три фути від усього стовбура.

                              Прошу тебе, швидше  мені скажи:

                              Яка висота  тополі?»

(Відповідь:8 м)

 

  Індивідуальне виконання.

1. Завдання з підручника "Арифметики" Леонтія Магницкого

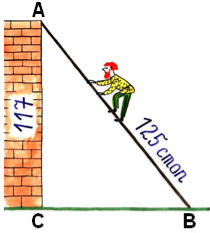    "Сталося  деякій людині до стіни сходи

     прибрати, стіни ж тієї висота була 117

     стоп. І узяв він драбину  завдовжки  125

     стоп.  І дізнатися він хоче, на скільки стоп, цю

     драбину  нижнім кінцем від стіни                                           

     відставити  треба".

(Відповідь: 44 стоп)

 

 

2. Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АC, АD однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягнута проволока, щоб  ялинка стояла вертикально? (Відповідь: 10метрів)
3. Дах будинку має форму рівнобедреного трикутника ( ABC) , AB= 50м, основа трикутника AC = 96 м . Знайти висоту даху. (Відповідь:14 метрів)
4. За 40м одна від однієї ростуть дві ялинки. Ви заміряли їх висоти: виявилося, що одна із них має висоту 31м, а інша, молода – 6м. Чи можете ви обчислити, якою є відстань між їхніми верхівками?

ІV. Домашнє завдання.

1. Повторити §16.
2. Виконати задачі, перейшовши за посиланням на QR-коді.
3. Скласти ментальну карту « Прямокутний трикутник»

 

ІV. Підсумок уроку.

Отже, сьогодні ви побачили застосування найвідомішої теореми планіметрії – теореми Піфагора. Тому люди пам'ятають Піфагора дві з половиною тисячі років. Ось чому серед знаменитих олімпійських чемпіонів він довго залишиться найвідомішим, тому що йому випало щастя перемогти не тільки супротивників, але й перемогти час.

    Причина популярності теореми Піфагора триєдина – це краса, простота і значущість.

Діти, попереду у вас ще багато різних теорем життєвих та геометричних. Можливо, з часом теорема Піфагора буде здаватися вам дуже простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему – теорему Піфагора, – цікаву, могутню, вічну. Дякую всім за урок!

А закінчити урок я хочу словами:

Життя – театр, а всі ми в нім актори,

Ми знаємо багато різних див,

Та пам’ятати будем Піфагора,

Що теорему «золоту» створив.

Ось і закінчився наш урок.

Час невпинно й швидко так летить.

Ви до знань зробили новий крок.

Хай у всьому завжди вам щастить!