Контрольні роботи з геометрії
Контрольна робота з теми: «Чотирикутники»
Варіант 1
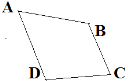 Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
- Правильна назва чотирикутника.
|
А |
Б |
В |
Г |
Д |
|
ADBC |
CDBA |
CADB |
CDAB |
ACBD |
-
Градусна міра одного з кутів паралелограма дорівнює 28
 . Знайдіть градусну міру інших його кутів.
. Знайдіть градусну міру інших його кутів.
|
А |
Б |
В |
Г |
Д |
|
28 |
28 |
28 |
28 |
28 |
- Як називається паралелограм у якого всі сторони рівні?
|
А |
Б |
В |
Г |
Д |
|
квадрат |
прямокутник |
рівнобічна трапеція |
трикутник |
парале-лограм |
-
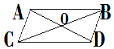 СABD – паралелограм, О – точка перетину діагоналей; СО=4 см, АО= 3 см. Знайдіть довжини OD i BC.
СABD – паралелограм, О – точка перетину діагоналей; СО=4 см, АО= 3 см. Знайдіть довжини OD i BC.
|
А |
Б |
В |
Г |
Д |
|
3 см, 6 см |
4 см, 8 см |
6 см, 8 см |
1,5см, 2см |
3 см, 8 см |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між чотирикутниками (1-4) і довжинами їхніх сторін (А-Д).
|
1 |
Сторони прямокутника, якщо одна із них на 4 більша за іншу, а периметр прямокутника дорівнює 28 |
А |
12; 20 |
|||||||
|
2 |
Сторони паралелограма, якщо їх різниця дорівнює 8, а периметр паралелограма дорівнює 64 |
Б |
5; 15 |
|||||||
|
3 |
Основи рівнобічної трапеції , якщо їх відношення дорівнює 1:3, бічна сторона – 10, а периметр – 40 |
В |
8 |
|||||||
|
4 |
Сторона ромба, периметр якого на 24 більший за його сторону |
Г |
5; 9 |
|||||||
|
|
|
Д |
10 |
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- О – точка перетину діагоналей ромба ABCD. Знайдіть градусну міру кутів ромба, якщо ےDAO у 5 разів менший за ےСВО.
- CBED – паралелограм, РCBED=60 см; ED:DC=7:8. Знайдіть довжину BE.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
-
У прямокутнику ABCD діагоналі AC і BD перетинаються в точці О, ےAOD=120
 . Знайдіть ےACD.
. Знайдіть ےACD.
- Доведіть, що трапеція рівнобічна, якщо кути при основі цієї трапеції рівні.
Контрольна робота з теми: «Чотирикутники»
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
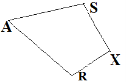 Правильна назва чотирикутника.
Правильна назва чотирикутника.
|
А |
Б |
В |
Г |
Д |
|
ARXS |
XSRA |
XARS |
AXSR |
ASRX |
-
Градусна міра одного з кутів паралелограма дорівнює 128
 . Знайдіть градусну міру інших його кутів.
. Знайдіть градусну міру інших його кутів.
|
А |
Б |
В |
Г |
Д |
|
128 |
128 |
128 |
128 |
128 |
- Як називається паралелограм у якого всі кути рівні?
|
А |
Б |
В |
Г |
Д |
|
ромб |
прямокутник |
рівнобічна трапеція |
трикутник |
парале-лограм |
-
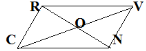 СRVN – паралелограм, О – точка перетину діагоналей; СО=6 см, RО= 4 см. Знайдіть довжини RN i NO.
СRVN – паралелограм, О – точка перетину діагоналей; СО=6 см, RО= 4 см. Знайдіть довжини RN i NO.
|
А |
Б |
В |
Г |
Д |
|
12см, 4 см |
12см, 8 см |
6 см, 4 см |
3 см, 2см |
8 см, 6 см |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між чотирикутниками (1-4) і довжинами їхніх сторін (А-Д).
|
1 |
Сторони прямокутника, якщо одна із них на 2 менша за іншу, а периметр прямокутника дорівнює 32 |
А |
10; 15 |
|||||||
|
2 |
Сторони паралелограма, якщо їх різниця дорівнює 5, а периметр паралелограма дорівнює 50 |
Б |
6; 12 |
|||||||
|
3 |
Основи рівнобічної трапеції , якщо їх відношення дорівнює 1:2, бічна сторона – 10, а периметр – 38 |
В |
6 |
|||||||
|
4 |
Сторона ромба, периметр якого на 18 більший за його сторону |
Г |
7; 9 |
|||||||
|
|
|
Д |
9 |
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- О – точка перетину діагоналей ромба ABCD. Знайдіть градусну міру кутів ромба, якщо ےDAO у 8 разів більший за ےСВО.
- EKMN – паралелограм, РEKMN=80 см; EN:NM=7:9. Знайдіть довжину KM.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
-
У ромбі ABCD ےA =60
 , BD=15 см. Знайдіть периметр ромба.
, BD=15 см. Знайдіть периметр ромба.
- Доведіть, що діагоналі рівнобічної трапеції рівні між собою.
Контрольна робота з теми: «Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції»
Варіант 1
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
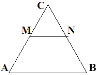 На рисунку АМ=МС, BN=NC, AB=6 см. Дожина відрізка MN=…
На рисунку АМ=МС, BN=NC, AB=6 см. Дожина відрізка MN=…
|
А |
Б |
В |
Г |
Д |
|
3 см |
4 см |
5 см |
6 см |
7 см |
-
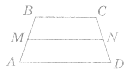 У трапеції ABCD (BC
У трапеції ABCD (BC AD) MN – середня лінія трапеції, AD=7 см, BC=3 см (див. рисунок). Тоді довжина відрізка MN=…
AD) MN – середня лінія трапеції, AD=7 см, BC=3 см (див. рисунок). Тоді довжина відрізка MN=…
|
А |
Б |
В |
Г |
Д |
|
3 см |
4 см |
5 см |
6 см |
7 см |
|
А |
Б |
В |
Г |
Д |
|
45 |
80 |
60 |
90 |
100 |
-
 Чому дорівнює градусна міра кута А, якщо ےС=100
Чому дорівнює градусна міра кута А, якщо ےС=100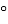 ?
?

- На рисунку AN=4, NK=3, PK=6. Знайдіть довжини AP.
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
6 |
7 |
10 |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
-
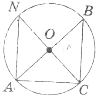 Установіть відповідність між центральними або вписаними кутами (1-4) і їхніми градусними мірами (А-Д), якщо О – центр кола.
Установіть відповідність між центральними або вписаними кутами (1-4) і їхніми градусними мірами (А-Д), якщо О – центр кола.
|
1 |
ےNAB, якщо ے BOC=70 |
А |
45 |
|||||||
|
2 |
ےANC, якщо ےBAC=50 |
Б |
50 |
|||||||
|
3 |
ےBAC, якщо ےABC=40 |
В |
40 |
|||||||
|
4 |
ے NAC |
Г |
90 |
|||||||
|
|
|
Д |
55 |
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Точки Р, К, Е – середини сторін ΔMCD. Периметр ΔMCD=36 см. Знайдіть периметр ΔPKE.
- Діагональ трапеції ділить середню лінію на відрізки 14 см та 8 см. Знайдіть довжини основ трапеції.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть периметр трапеції, описаної навколо кола, якщо її основи дорівнюють 5 см і 7 см.
-
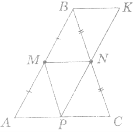 Використовуючи рисунок, доведіть теорему про середню лінію трикутника, враховуючи, що РК||АВ, ВК||АС.
Використовуючи рисунок, доведіть теорему про середню лінію трикутника, враховуючи, що РК||АВ, ВК||АС.
Контрольна робота з теми: «Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції»
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
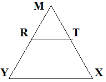 На рисунку YR=RМ, MT=TX, RT=5 см. Дожина відрізка XY=…
На рисунку YR=RМ, MT=TX, RT=5 см. Дожина відрізка XY=…
|
А |
Б |
В |
Г |
Д |
|
1 см |
2,5 см |
5 см |
7,5 см |
10 см |
-
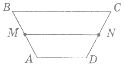 У трапеції ABCD (BC
У трапеції ABCD (BC AD) MN – середня лінія трапеції, AD=4 см, BC=6 см (див. рисунок). Тоді довжина відрізка MN=…
AD) MN – середня лінія трапеції, AD=4 см, BC=6 см (див. рисунок). Тоді довжина відрізка MN=…
|
А |
Б |
В |
Г |
Д |
|
3 см |
4 см |
5 см |
6 см |
7 см |
-
Чому дорівнює градусна міра кута В, якщо ے D=110

|
А |
Б |
В |
Г |
Д |
|
45 |
70 |
60 |
90 |
110 |

- На рисунку AР=11, NK=7, AN=6. Знайдіть довжини PK.
|
А |
Б |
В |
Г |
Д |
|
6 |
7 |
9 |
11 |
12 |
 Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
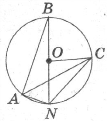
- Установіть відповідність між центральними або вписаними кутами (1-4) і їхніми градусними мірами (А-Д), якщо О – центр кола.
|
1 |
ےNAB |
А |
60 |
|||||||
|
2 |
ےANB, якщо ےACN=30 |
Б |
70 |
|||||||
|
3 |
ےBOC, якщо ےBNC=40 |
В |
80 |
|||||||
|
4 |
ے BNC, якщо ے CAN=20 |
Г |
50 |
|||||||
|
|
|
Д |
90 |
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Точки M, N, К – середини сторін ΔCDE. Периметр ΔMNK=24 см. Знайдіть периметр ΔECD.
- Довжини основ трапеції 18 см та 12 см. Знайдіть відрізки, на які діагональ ділить середню лінію.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть периметр трапеції, описаної навколо кола, якщо її бічні сторони дорівнюють 9 см і 10 см.
-
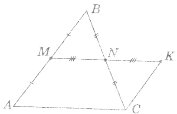 Використовуючи рисунок, доведіть теорему про середню лінію трикутника, враховуючи, що MN=NK.
Використовуючи рисунок, доведіть теорему про середню лінію трикутника, враховуючи, що MN=NK.
Контрольна робота з теми: «Подібність трикутників»
Варіант 1
 Частина 1. У завданнях 1 – 4 позначте одну правильну, на вашу думку, відповідь.
Частина 1. У завданнях 1 – 4 позначте одну правильну, на вашу думку, відповідь.
- Трикутники АВС і А1В1С1 – подібні. Знайдіть у.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
4 |
-
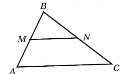 На рисунку МN || АС. Знайти АМ, якщо АВ = 6см, МN = 4см, АС = 12см.
На рисунку МN || АС. Знайти АМ, якщо АВ = 6см, МN = 4см, АС = 12см.
|
А |
Б |
В |
Г |
Д |
|
|
|
3 см |
6 см |
Визначити неможливо |
-
Сторони трикутника дорівнюють
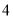 см,
см, 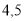 см і
см і 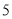 см. Знайдіть сторони подібного йому трикутника, найбільша сторона якого дорівнює
см. Знайдіть сторони подібного йому трикутника, найбільша сторона якого дорівнює  см.
см.
|
А |
Б |
В |
Г |
Д |
|
15см,17 см, 20 см |
19 см, 20 см, 19,5 см |
16 см, 18 см, 20 см |
20 см, 21 см, 22 см |
20 см, 25 см, 22,5 см |
- Які з наведених наборів відрізків є сторонами подібних трикутників?
|
А |
Б |
В |
Г |
Д |
|
4, 6, 9 і 12, 18, 36 |
3, 4, 5 і 15, 12, 25 |
11,13, 15 і 5,5; 6,5; 9 |
12, 14, 20 і 6, 7, 5 |
3, 5, 6 і 6, 10, 12 |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
-
Установіть відповідність між подібними трикутниками
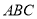 і
і 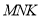 (1 – 4) та невідомими кутами даних трикутників (А – Д).
(1 – 4) та невідомими кутами даних трикутників (А – Д).
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
|
Г |
|
|
|
|
Д |
|
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
6. Два кути одного трикутника дорівнюють двом кутам другого трикутника. Знайдіть сторони другого трикутника, якщо його периметр дорівнює ![]() см, а сторони першого трикутника дорівнюють
см, а сторони першого трикутника дорівнюють ![]() см,
см, ![]() см,
см, ![]() см.
см.
7. Гострі кути двох прямокутних трикутників відповідно рівні. Гіпотенуза і катет одного трикутника дорівнюють 20 см і 16 см. Знайдіть відповідний катет другого трикутника, якщо його гіпотенуза 30 см.
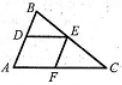 Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
8. У трикутник ![]() вписано паралелограм
вписано паралелограм ![]() . Знайдіть
. Знайдіть ![]() , якщо
, якщо ![]() см,
см, ![]() см,
см, ![]() см.
см.
9. Основи прямокутної трапеції дорівнюють 14 см і 24 см, а більша діагональ є бісектрисою прямого кута. Знайдіть периметр трапеції.
Контрольна робота з теми: «Подібність трикутників»
Варіант 2
 Частина 1. У завданнях 1 – 4 позначте одну правильну, на вашу думку, відповідь.
Частина 1. У завданнях 1 – 4 позначте одну правильну, на вашу думку, відповідь.
- Трикутники АВС і А1В1С1 – подібні. Знайдіть х.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
4 |
-
 На рисунку МN || АС. Знайти АМ, якщо ВС = 12см, МN = 3 см, АС = 24 см.
На рисунку МN || АС. Знайти АМ, якщо ВС = 12см, МN = 3 см, АС = 24 см.
|
А |
Б |
В |
Г |
Д |
|
18 см |
|
3 см |
6 см |
Визначити неможливо |
-
Сторони трикутника дорівнюють
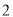 см,
см, 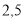 см і
см і 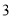 см. Знайдіть сторони подібного йому трикутника, найменша сторона якого дорівнює 6 см.
см. Знайдіть сторони подібного йому трикутника, найменша сторона якого дорівнює 6 см.
|
А |
Б |
В |
Г |
Д |
|
15см,17 см, 20 см |
19 см, 20 см, 19,5 см |
16 см, 18 см, 20 см |
20 см, 21 см, 22 см |
20 см, 25 см, 22,5 см |
- Які з наведених наборів відрізків є сторонами подібних трикутників?
|
А |
Б |
В |
Г |
Д |
|
4, 6, 9 і 12, 18, 27 |
3, 5, 6 і 7, 10, 12 |
5, 4, 5 і 12, 15, 25 |
12, 14, 20 і 6, 7, 5 |
3, 5, 6 і 6, 10, 15 |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
-
Установіть відповідність між подібними трикутниками
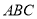 і
і 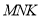 (1 – 4) та невідомими кутами даних трикутників (А – Д).
(1 – 4) та невідомими кутами даних трикутників (А – Д).
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
|
Г |
|
|
|
|
Д |
|
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
6. Два кути одного трикутника дорівнюють двом кутам другого трикутника. Знайдіть сторони другого трикутника, якщо його периметр дорівнює ![]() см, а сторони першого трикутника дорівнюють 5 см, 6 см, 7 см.
см, а сторони першого трикутника дорівнюють 5 см, 6 см, 7 см.
7. Катети прямокутного трикутника завдовжки 10 см і 24 см відповідно пропорційні катетам іншого прямокутного трикутника. Знайдіть катет другого трикутника, якщо його менший катет 20 см.
 Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
8. У трикутник ![]() вписано паралелограм DQCM, якщо AC=10 см, MC = 4 см, QC=9 см. Знайдіть BC.
вписано паралелограм DQCM, якщо AC=10 см, MC = 4 см, QC=9 см. Знайдіть BC.
9. Основи прямокутної трапеції дорівнюють 24 см і 34 см, а менша діагональ є бісектрисою прямого кута. Знайдіть периметр трапеції.
Контрольна робота з теми: «Теорема Піфагора»
Варіант 1
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
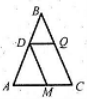
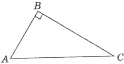
 Враховуючи, що відповідно до теореми Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів, теорема Піфагора для трикутника АВС, зображеного на рисунку, має вигляд:
Враховуючи, що відповідно до теореми Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів, теорема Піфагора для трикутника АВС, зображеного на рисунку, має вигляд:
|
А |
Б |
В |
|
АВ2=ВС2+АС2 |
ВС2=АВ2+АС2 |
АС2=АВ2+ВС2 |
|
Г |
Д |
|
|
АВ2=ВС2-АС2 |
АС2=АВ2-ВС2 |
|
- Якщо катети прямокутного трикутника дорівнюють 4 см і 5 см, то квадрат гіпотенузи дорівнює:
|
А |
Б |
В |
Г |
Д |
|
(4+5)2 |
(4-5)2 |
52-42 |
42-52 |
42+52 |
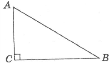
-
Знайдіть сторону АВ прямокутного трикутника АВС, якщо АС=1 см, ВС=2 см,
 С=90
С=90 .
.
|
А |
Б |
В |
Г |
Д |
|
3 см |
|
1,5 см |
|
5 см |
- Чи можуть сторони прямокутного трикутника дорівнювати 6 см, 7 см, 8 см?
|
А |
Б |
В |
|
|
так |
ні |
Визначити неможливо |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між елементами прямокутних трикутників (1-4) і їхніми значеннями (А-Д).
|
1 |
Основу, якщо бічна сторона рівнобедреного трикутника 10 см, а висота 6 |
А |
|
|||||||
|
2 |
Сторону ромба, діагоналі якого дорівнюють 2 і 4 |
Б |
13 |
|||||||
|
3 |
Діагональ прямокутника, якщо його сторони дорівнюють 5 і 12 |
В |
|
|||||||
|
4 |
Катет, якщо гіпотенуза і катет дорівнюють |
Г |
5 |
|||||||
|
|
|
Д |
1 |
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Точки M, N, К – середини сторін ΔCDE. Периметр ΔMNK=24 см. Знайдіть периметр ΔECD.
- Довжини основ трапеції 18 см та 12 см. Знайдіть відрізки, на які діагональ ділить середню лінію.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть периметр трапеції, описаної навколо кола, якщо її бічні сторони дорівнюють 9 см і 10 см.
- Два кола, радіуси яких 4 см і 9 см, мають зовнішній дотик. Пряма дотикається до цих кіл у точках С і D. Знайдіть СD
Контрольна робота з теми: «Теорема Піфагора»
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
 Враховуючи, що відповідно до теореми Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів, теорема Піфагора для трикутника АВС, зображеного на рисунку, має вигляд:
Враховуючи, що відповідно до теореми Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів, теорема Піфагора для трикутника АВС, зображеного на рисунку, має вигляд:
|
А |
Б |
В |
|
АВ2=ВС2+АС2 |
ВС2=АВ2+АС2 |
АС2=АВ2+ВС2 |
|
Г |
Д |
|
|
АВ2=ВС2-АС2 |
АС2=АВ2-ВС2 |
|
- Якщо катети прямокутного трикутника дорівнюють 5 см і 12 см, то гіпотенуза дорівнює:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайдіть сторону АВ прямокутного трикутника АВС, якщо АС=2 см, ВС=
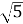 см,
см, 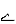 С=90
С=90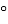 .
.
|
А |
Б |
В |
Г |
Д |
|
3 см |
|
2 см |
|
5 см |
- Чи можуть сторони прямокутного трикутника дорівнювати 10 см, 8 см, 6 см?
|
А |
Б |
В |
|
|
так |
ні |
Визначити неможливо |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між елементами прямокутних трикутників (1-4) і їхніми значеннями (А-Д).
|
1 |
Сторону ромба, діагоналі якого дорівнюють 14 і 48 |
А |
1 |
|||||||
|
2 |
Катет, якщо гіпотенуза і катет дорівнюють |
Б |
25 |
|||||||
|
3 |
Сторону квадрата, діагональ якого дорівнює 2 |
В |
|
|||||||
|
4 |
Бічну сторону рівнобедреного трикутника, якщо висота 5, а основа 24 |
Г |
13 |
|||||||
|
|
|
Д |
|
|||||||
|
|
А |
Б |
В |
Г |
Д |
|||||
|
1 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Точки M, N, К – середини сторін ΔCDE. Периметр ΔMNK=24 см. Знайдіть периметр ΔECD.
- Довжини основ трапеції 18 см та 12 см. Знайдіть відрізки, на які діагональ ділить середню лінію.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть периметр трапеції, описаної навколо кола, якщо її бічні сторони дорівнюють 9 см і 10 см.
- Два кола, радіуси яких 5 см і 20 см, мають зовнішній дотик. Пряма дотикається до цих кіл у точках С і D. Знайдіть СD.
Контрольна робота з теми: «Розв’язування прямокутних трикутників»
Варіант 1
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
 Враховуючи, що косинус гострого кута в прямокутному трикутнику дорівнює відношенню прилеглого катета до гіпотенузи, і користуючись рисунком, виберіть значення для косинуса кута С.
Враховуючи, що косинус гострого кута в прямокутному трикутнику дорівнює відношенню прилеглого катета до гіпотенузи, і користуючись рисунком, виберіть значення для косинуса кута С.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
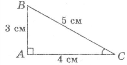
 Враховуючи, що синус гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузи, і користуючись рисунком, виберіть значення для синуса кута А.
Враховуючи, що синус гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузи, і користуючись рисунком, виберіть значення для синуса кута А.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
 Враховуючи, що тангенс гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до прилеглого, і користуючись рисунком, виберіть значення для тангенса кута В.
Враховуючи, що тангенс гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до прилеглого, і користуючись рисунком, виберіть значення для тангенса кута В.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
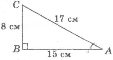
Вираз
 дорівнює:
дорівнює:
|
А |
Б |
В |
Г |
Д |
|
|
|
1 |
2 |
3 |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність за означенням
|
1 |
tg α |
А |
відношення прилеглого катета до гіпотенузи |
|||||
|
2 |
|
Б |
відношення гіпотенузи до протилежного катета |
|||||
|
3 |
|
В |
відношення |
|||||
|
4 |
ctg α |
Г |
відношення |
|||||
|
|
|
Д |
відношення протилежного катета до гіпотенузи |
|||||
|
|
А |
Б |
В |
Г |
Д |
|||
|
1 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
Частина 3. Завдання 6 виконайте на чернетці та запишіть тільки правильну відповідь.
-
Спростіть вирази: а)
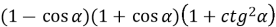 , б)
, б) 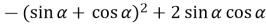 .
.
Частина 4. У завданнях 7, 8 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
-
Знайдіть гострий кут ромба, якщо його діагоналі
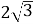 см і 2 см.
см і 2 см.
-
Кут при вершині рівнобедреного трикутника дорівнює
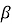 , а бічна сторона – b. Знайдіть периметр трикутника.
, а бічна сторона – b. Знайдіть периметр трикутника.
Контрольна робота з теми: «Розв’язування прямокутних трикутників»
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
-
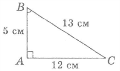 Враховуючи, що косинус гострого кута в прямокутному трикутнику дорівнює відношенню прилеглого катета до гіпотенузи, і користуючись рисунком, виберіть значення для косинуса кута В.
Враховуючи, що косинус гострого кута в прямокутному трикутнику дорівнює відношенню прилеглого катета до гіпотенузи, і користуючись рисунком, виберіть значення для косинуса кута В.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
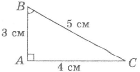 Враховуючи, що синус гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузи, і користуючись рисунком, виберіть значення для синуса кута В.
Враховуючи, що синус гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузи, і користуючись рисунком, виберіть значення для синуса кута В.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
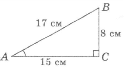 Враховуючи, що тангенс гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до прилеглого, і користуючись рисунком, виберіть значення для тангенса кута А.
Враховуючи, що тангенс гострого кута в прямокутному трикутнику дорівнює відношенню протилежного катета до прилеглого, і користуючись рисунком, виберіть значення для тангенса кута А.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Вираз
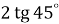 дорівнює:
дорівнює:
|
А |
Б |
В |
Г |
Д |
|
|
|
1 |
2 |
3 |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність за означенням
|
1 |
tg α |
А |
відношення протилежного катета до гіпотенузи |
|
2 |
|
Б |
відношення протилежного катета до прилеглого |
|
3 |
|
В |
відношення прилеглого катета до гіпотенузи |
|
4 |
ctg α |
Г |
відношення гіпотенузи до прилеглого катета |
|
|
|
Д |
відношення прилеглого катета до протилежного |
Частина 3. Завдання 6 виконайте на чернетці та запишіть тільки правильну відповідь.
-
Спростіть вирази: а)
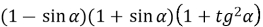 ,
,
б) ![]() .
.
Частина 4. У завданнях 7, 8 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
-
Сторони прямокутника дорівнюють 3 см і
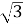 см. Знайдіть кут, який утворює діагональ із меншою стороною.
см. Знайдіть кут, який утворює діагональ із меншою стороною.
-
Кут при основі рівнобедреного трикутника дорівнює
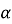 , а бічна сторона – b. Знайдіть периметр трикутника.
, а бічна сторона – b. Знайдіть периметр трикутника.
Контрольна робота з теми: «Многокутники. Площі многокутників»
Варіант 1
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
- Сума градусних мір кутів восьмикутника дорівнює.
|
А |
Б |
В |
Г |
Д |
|
720о |
1440о |
480о |
360о |
1080о |
- Скільки сторін має многокутник, якщо градусна міра кожного із його зовнішніх кутів дорівнює 72о.
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
5 |
6 |
7 |
- Знайти площу квадрата зі стороною 12 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
24 см |
136 см |
144 см |
224 см |
- Знайдіть градусні міри кутів п’ятикутника, якщо вони відносяться як 4:5:6:12:9.
|
А |
Б |
В |
Г |
Д |
|
40о,50о, 60о,120о, 90о |
60о,75о, 90о,180о, 135о |
20о,25о, 30о,60о, 45о |
80о,100о, 120о,240о, 180о |
4о,5о,6о, 12о,9о |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між фігурами і формулами площі.
|
1 |
Площа ромба |
А |
|
|||||
|
2 |
Площа паралелограма |
Б |
S=ab |
|||||
|
3 |
Площа прямокутного трикутника |
В |
|
|||||
|
4 |
Площа прямокутника |
Г |
S=aha |
|||||
|
|
|
Д |
|
|||||
|
|
А |
Б |
В |
Г |
Д |
|||
|
1 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
Частина 3. Завдання 6 виконайте на чернетці та запишіть тільки правильну відповідь.
- Обчисліть площу трапеції з довжинами основ 6 см, і 8 см і висотою – 4 см.
- Основа трикутника дорівнює 16 см, а висота – 22 см. Знайдіть площу трикутника, утвореного середніми лініями даного трикутника.
Частина 4. У завданнях 7, 8 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть площу прямокутної трапеції, гострий кут якої дорівнює 30о, а більша бічна сторона – 10 см, якщо в цю трапецію можна вписати коло.
- Довжини висот паралелограма 5 см і 3 см. Знайдіть довжину сторони паралелограма, до якої проведено меншу висоту, якщо довжина сусідньої сторони 9 см.
Контрольна робота з теми: «Многокутники. Площі многокутників»
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
- Сума градусних мір кутів десятикутника дорівнює.
|
А |
Б |
В |
Г |
Д |
|
900о |
1440о |
600о |
360о |
1080о |
- Скільки сторін має многокутник, якщо градусна міра кожного із його зовнішніх кутів дорівнює 45о.
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
7 |
8 |
9 |
- Знайти площу квадрата зі стороною 10 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
24 см |
100 см |
144 см |
224 см |
- Знайдіть градусні міри кутів шестикутника, якщо вони відносяться як 1:3:4:6:10:12.
|
А |
Б |
В |
Г |
Д |
|
10о,30о, 40о,60о, 100о,120о |
15о,45о, 60о,90о, 150о,180о |
20о,60о, 80о,120о, 200о, 240о |
1о,3о, 4о,6о, 10о,12о |
5о,15о, 20,30о, 50о,60о |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між фігурами і формулами площі.
|
1 |
Площа квадрата |
А |
|
|||||
|
2 |
Площа ромба |
Б |
S=a2 |
|||||
|
3 |
Площа трикутника |
В |
|
|||||
|
4 |
Площа трапеції |
Г |
S= |
|||||
|
|
|
Д |
|
|||||
|
|
А |
Б |
В |
Г |
Д |
|||
|
1 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Обчисліть площу трапеції з довжинами основ 7 см, і 9 см і висотою – 6 см.
- Основа трикутника дорівнює 16 см, а висота – 10 см. Знайдіть площу трикутника, утвореного середніми лініями даного трикутника.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Знайдіть площу прямокутної трапеції, гострий кут якої дорівнює 30о, а висота – 10 см, якщо в цю трапецію можна вписати коло.
- Довжини сторін паралелограма 6 см і 8 см. Довжина висоти, проведеної до меншої сторони, 4см. Знайдіть довжину висоти, проведеної до більшої сторони.
Підсумкова контрольна робота
Варіант 1
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
- Знайдіть довжину другої сторони паралелограма, якщо довжина однієї сторони дорівнює 8 см, а периметр – 34 см.
|
А |
Б |
В |
Г |
Д |
|
26 см |
9 см |
13 см |
50 см |
25 см |
-
Знайдіть величину вписаного кута, що спирається на дугу кола, рівну
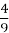 кола
кола
|
А |
Б |
В |
Г |
Д |
|
160о |
320о |
80о |
70о |
20о |
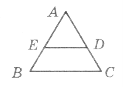
-
Дано
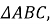 ED||DC; AD=10см, DC=12 см, EB=18см. Знайдіть довжину AE.
ED||DC; AD=10см, DC=12 см, EB=18см. Знайдіть довжину AE.
|
А |
Б |
В |
Г |
Д |
|
4 см |
10 см |
12 см |
18 см |
15 см |
- Катети прямокутного трикутника дорівнюють 12 см і 5 см. Знайдіть периметр трикутника.
|
А |
Б |
В |
Г |
Д |
|
15 см |
17 см |
20 см |
30 см |
60 см |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між площами многокутників і їхніми числовими значеннями.
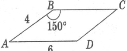

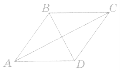
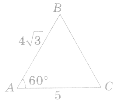
рис. 1 рис. 2 рис. 3 рис. 4
|
1 |
Площа Δ АВС (рис. 1) |
А |
48 |
|||||
|
2 |
Площа ромба ABCD (рис. 2), якщо його діагоналі – 12 і 8 |
Б |
24 |
|||||
|
3 |
Площа квадрата ABCD (рис. 3), якщо його діагональ 2 |
В |
4 |
|||||
|
4 |
Площа паралелограма ABCD (рис. 4) |
Г |
12 |
|||||
|
|
|
Д |
15 |
|||||
|
|
А |
Б |
В |
Г |
Д |
|||
|
1 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Катети прямокутного трикутника відносяться як 3:4, а його периметр дорівнює 48 см. Знайти медіану, яка виходить з прямого кута.
- Знайдіть ےABC ромба ABCD, якщо ےBAC=28о.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
-
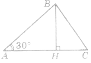 Діагональ рівнобічної трапеції є бісектрисою гострого кута. Знайдіть периметр трапеції, якщо довжини її основ дорівнюють 5 см і 10 см.
Діагональ рівнобічної трапеції є бісектрисою гострого кута. Знайдіть периметр трапеції, якщо довжини її основ дорівнюють 5 см і 10 см.
- У ΔАВС: ВН – висота, ےВАС=30О, ВС=4 см, СН=1см. Знайдіть довжину АН.
Підсумкова контрольна робота
Варіант 2
Частина 1. У завданнях 1 – 4 позначте одну правильну відповідь.
- Знайдіть довжину другої сторони прямокутника, якщо довжина однієї сторони дорівнює 9 см, а периметр – 44 см.
|
А |
Б |
В |
Г |
Д |
|
35 см |
26 см |
13 см |
62 см |
54 см |
-
Знайдіть величину вписаного кута, що спирається на дугу кола, рівну
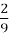 кола.
кола.
|
А |
Б |
В |
Г |
Д |
|
80о |
40о |
160о |
20о |
100о |
-
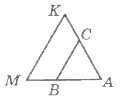 Дано
Дано 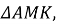 BC||MK; AB=10см, MB=12 см, AC=15 см. Знайдіть довжину KC.
BC||MK; AB=10см, MB=12 см, AC=15 см. Знайдіть довжину KC.
|
А |
Б |
В |
Г |
Д |
|
15 см |
23 см |
12 см |
18 см |
10 см |
- Гіпотенуза прямокутного трикутника дорівнює 13 см, а катет – 12 см. Знайдіть периметр трикутника.
|
А |
Б |
В |
Г |
Д |
|
15 см |
20 см |
25 см |
30 см |
60 см |
Частина 2. У завданні 5 до кожного рядка, позначеного цифрою, доберіть один правильний, на вашу думку, варіант, позначений буквою, і поставте позначки в бланку відповідей на перетині відповідних рядків і стовпців.
- Установіть відповідність між площами многокутників і їхніми числовими значеннями.
![]()
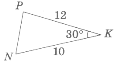 рис. 1 рис. 2 рис. 3 рис. 4
рис. 1 рис. 2 рис. 3 рис. 4
|
1 |
Площа Δ NPK (рис. 1) |
А |
6 |
|||||
|
2 |
Площа ромба NPKM (рис. 2), якщо його діагоналі – 4 і 8 |
Б |
12 |
|||||
|
3 |
Площа квадрата NPKM (рис. 3), якщо його діагональ 2 |
В |
30 |
|||||
|
4 |
Площа паралелограма NPKM (рис. 4) |
Г |
16 |
|||||
|
|
|
Д |
24 |
|||||
|
|
А |
Б |
В |
Г |
Д |
|||
|
1 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
Частина 3. Завдання 6, 7 виконайте на чернетці та запишіть тільки правильну відповідь.
- Гіпотенуза і катет прямокутного трикутника відносяться як 5:4, а другий катет дорівнює 12 см. Знайти медіану, яка виходить з прямого кута.
- Знайдіть ےDCF ромба CDEF, якщо ےDEC=37о.
Частина 4. У завданнях 8, 9 наведіть повне розв’язання (за потреби користуйтеся чернеткою).
- Бісектриса кута прямокутника ділить його сторону у відношенні 3:2, починаючи з вершини протилежного кута. Знайдіть довжини сторін прямокутника, якщо його периметр 28 см.
-
У ΔСКА: CD – висота, ےАСD=30О, СK=12 см, DK=3
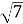 см. Знайдіть довжину АD.
см. Знайдіть довжину АD.
1
-
-
-
дуже добре


про публікацію авторської розробки
Додати розробку
