Конспект уроку "Тригонометричні тотожності"

Урок №5. Тема:  Тригонометричні тотожності

Формування компетентностей:

предметна компетентність:

• розглянути тригонометричну тотожність та наслідок із неї;
• розвивати вміння перетворювати тригонометричні вирази за допомогою тригонометричних тотожностей;

ключові компетентності:

• спілкування державною мовою – уміння доречно та коректно вживати в

мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;

• математична компетентність – уміння оперувати числовою інформацією;
• уміння вчитися впродовж життя – уміння оцінювати результати своєї

навчальної діяльності.

Тип уроку: засвоєння вмінь та навичок.

Обладнання та наочність: підручник з геометрії за 9 клас, автори: Мерзляк, Полонський, Якір, 2017 р.

Хід уроку

I. Організаційний момент.

• Налаштовування на роботу.
• Перевірка домашнього завдання:

(§1 п.1 № 1.3, 1.9)

№1.3. Кути і суміжні, ;

1. Знайдіть .

.

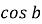2. Який із кутів 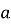і 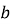є гострим, а який — тупим?

– тупий кут, – гострий кут.

№1.9 Знайдіть ,

;

;

.

II. Актуалізація опорних знань.

Фронтальне опитування

1. Сформулюйте означення синуса, косинуса, тангенса кутів від 0° до 180°.
2. Користуючись таблицею (або калькулятором), знайдіть:

a)  б) °;

в) °.

Мотивація навчальної діяльності учнів

Поштовхом до інтелектуальної діяльності учнів може слугувати запропоноване вчителем завдання.

Завдання. Виконайте зображення прямокутного трикутника з катетами і гіпотенузою . Кути, протилежні катетам , позначте відповідно α, β. Запишіть відношення, яким дорівнюють та . Порівняйте записані відношення. Що ви помітили? Чи зміниться результат, якщо взяти інший прямокутний трикутник? Сформулюйте здобутий результат у вигляді твердження.

Мета запропонованого завдання — наочно продемонструвати учням існування певних залежностей між тригонометричними функціями деякого гострого кута. Далі вчитель наголошує на тому, що для інших тригонометричних функцій (крім тангенса і котангенса) одного й того самого кута також існують певні залежності; їх вивчення і становить основну мету уроку.

План вивчення нового матеріалу

1. Основна тригонометрична тотожність.
2. Наслідок з основної тригонометричної тотожності.
3. Співвідношення для тангенса і котангенса одного й того самого го-строго кута прямокутного трикутника.

Опорний конспект

Основна тригонометрична тотожність

Слід зазначити, що основну тригонометричну тотожність
 

у восьмому класі доведено для гострого кута α. Покажемо, що ця тотожність справедлива для будь-якого кута ° до 180°.

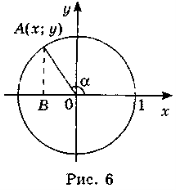
Якщо кут α — тупий (рис. 6), тоді із прямокутного трикутни­ка

за теоремою Піфагора маємо: ОВ² + АВ² = =ОА², (-x)² + у² = 1, х² + у² = 1. Ураховуючи, що , , маємо sin²α+ + cos²α = 1.

Якщо α = 0°, тоді ² 0° + ² 0° = 1² + 0² = l.

Якщо α = 90°, тоді ² 90° + ² 90° = 0² + 1² = 1.

Якщо α = 180°, тоді ² 180° + ² 180° = (-1)² + 0² = 1.

Отже, для будь-якого кута α (0° < α < 180°) виконується тотожність

² α + ² α = 1.

Формули доповнення

У 8-му класі для гострого кута було доведено формули доповнення, які виражають функції кута 90°- α через функції кута α. Нагадаємо їх:

Наприклад,

Слід зазначити, що ці формули справедливі і для тупого кута a, проте це спричинює необхідність вводити тригонометричні функції від'ємних кутів. Із цим матеріалом учні ознайомляться в 10-му класі.

Формули

Розглянемо коло з центром О у початку координат і радіу­сом 1. Відкладемо кут α — гострий кут, який утворює радіус кола з додатною віссю Ох. Побудуємо кут 180°- α. Для цього відкладемо кут В₁ОА₁ від від'ємної півосі Ох, тоді A₁OB = 180° - α (рис. 7).

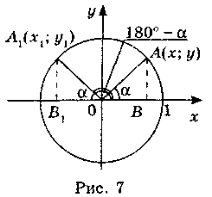
Нехай координати точок А і А₁ відповідно (х; у) і (х₁; у₁), ∆ОВА = ∆ОВ₁А₁ (за гіпотенузою і гострим кутом). Тоді sin (180°- α) = y₁ = y = sinα, cos (180°-α) = = х₁ = - x = - cos α, tg (180°- α) = = = = - tg α. Ці формули дають можливість, знаючи значення тригонометричних функцій гострих кутів, знаходити значен­ня тригонометричних функцій тупих кутів.

Наприклад,

IV. Засвоєння нових знань і способів дій

№ 1.13. Чи є правильним твердження (відповідь обґрунтуйте):

1. косинус гострого кута більший за косинус тупого кута;
2. існує тупий кут, синус і косинус якого рівні;
3. існує кут, синус і косинус якого дорівнюють нулю;
4. косинус кута трикутника може дорівнювати від’ємному числу;
5. синус кута трикутника може дорівнювати від’ємному числу;
6. косинус кута трикутника може дорівнювати нулю;
7. синус кута трикутника може дорівнювати нулю;
8. косинус кута трикутника може дорівнювати –1;
9. синус кута трикутника може дорівнювати 1;
10. синус кута, відмінного від прямого, менший від синуса прямого кута;
11. косинус розгорнутого кута менший від косинуса кута, відмінного від розгорнутого;
12. синуси суміжних кутів рівні;
13. косинуси нерівних суміжних кутів є протилежними числами;
14. якщо косинуси двох кутів рівні, то рівні й самі кути;
15. якщо синуси двох кутів рівні, то рівні й самі кути;
16. тангенс гострого кута більший за тангенс тупого кута?

№ 1.15. Знайдіть значення виразу:

1. 
2. 
3. .

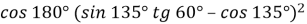№1.17. Знайдіть значення виразу, не користуючись калькулятором:

1. ;
2. ;
3. .

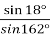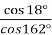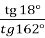№1.19. Знайдіть суму квадратів синусів усіх кутів прямокутного трикутника.

V. Підбиття підсумків уроку, рефлексія

• Яке півколо називається одиничним?
• Косинус і синус кута 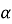, 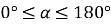– це …
• Чи існує кут 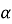, , 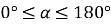для якого 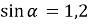? Поясніть, чому?
• Чому дорівнює ? ?
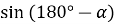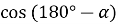• Чому дорівнює ?

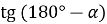VI. Домашнє завдання
(§1 п.1 № 1.16, 1.20)