Конспект уроку з алгебри 10 клас "Розв’язування прикладних задач на знаходження найбільшого і найменшого значення функцій"
Про матеріал
Конспект уроку для дистанційного навчання з алгебри 10 клас на тему: "Розв’язування прикладних задач на знаходження найбільшого і найменшого значення функцій".
Перегляд файлу
Конспект уроку для дистанційного навчання з алгебри 10 клас
Учитель: Доброго дня, шановні діти! Сьогодні ми будемо з вами розглядати дуже цікаву тему. А саме:
Тема: Розв’язування прикладних задач на знаходження найбільшого і найменшого значення функцій.
Учитель: Пропоную Вам опрацювати теоретичний матеріал до теми уроку.
1. Розглянемо спочатку поняття прикладних задач.
Розв’язування прикладних задач методами математики, як правило, містить три основні етапи:
1) Формалізацію, тобто тобто створення математичної моделі задачі ( переклад умови на мову математики);
2) Розв’язування складеної математичної задачі;
3) Інтерпретацію знайденого розв’язку.
Із прикладними задачами ви знайомі починаючи з 5 класу. Це задачі на рух, роботу, площу тощо.
Якщо говорити про задачі на знаходження найбільшого та найменшого значень реалізацію цих етапів можна проводити за схемою:
1) Одну з величин, яку потрібно знайти позначити через х.
2) Величину, про яку йдеться, що вона найбільша або найменша , виразити як функцію від х.
3) Дослідити одержану функцію на найбільше або найменше значення.
4) Упевнитися, що одержаний результат має зміст для початкової задачі .
Учитель: Давайте з Вами розглянемо приклади розв’язування прикладних задач
Приклад 1.
Число 10 подайте у вигляді суми двох невід’ємних доданків так, щоб сума квадратів цих чисел була найменшою
Розв’язання
Отже, ми маємо два числа сума яких дорівнює 10.
Тому нехай перший доданок буде х, тоді другий (10-х). Слідуючи умові ми маємо, що 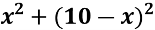 , який за умовою має бути найменшим.
, який за умовою має бути найменшим.
Відповідно найменше це значення виразимо через функцію залежну від даного х.
І маємо 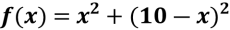
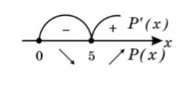
Далі користуючись похідною нам потрібно знайти найменше значення функції. Це ми робили з вами на попередніх уроках. Але є ще один момент . Чогось не вистачає для знаходження найменшого значення? А не вистачає проміжка. Як його знайти? А знайдемо ми його користуючись безпосередньо умовою .В умові сказано, що число 10 подати у вигляді суми двох чисел. Тобто це може бути , наприклад
Сума чисел 0+10=10, 1+9=10 5+5=10 6+4 =10 і так далі. Тобто ми можемо сказати що під х ми розглянемо числа від 0 до 10. Ось ми і отримали проміжок х є [0;10].
І маємо 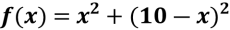 на проміжку
на проміжку
х є [0;10].
Далі розглянемо алгоритм знаходження найменшого значення.
1) D(y)=R;
2) 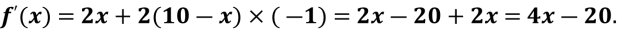
3) 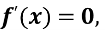
4) Знайдемо значення функції на кінцях відрізка і в даній точці.
5) Запишемо найменше значення функції.
 , що х1=х2=5.
, що х1=х2=5.
Приклад 2
З усіх прямокутників, площа яких дорівнює 25 см2, знайдіть прямокутник із найменшим периметром.
Розв’язання.
Пригадаємо про формулу для площі прямокутника.
Але в нашій задачі сторони невідомі, але відома площа.
Тому нехай одна сторона а буде х, а друга сторона b 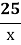 (значення вивели користуючись формулою площі користуючись формулою площі).
(значення вивели користуючись формулою площі користуючись формулою площі).
Оскільки нам потрібно знайти периметр (сума всіх сторін), то саме його ми представимо у вигляді функції залежної від х.
Тобто 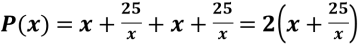 .
.
Функцію ми знайшли, і нам потрібно знайти проміжок , Проміжок буде х є [0;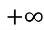 ].
].
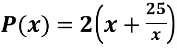 х є [0;
х є [0;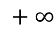 ).
).
Далі розглянемо алгоритм знаходження найменшого значення.
1) 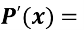 2
2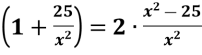 ;
;
2) 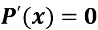
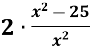 =0
=0
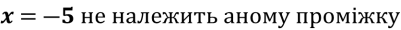 .
.
3) 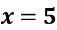 - точка мінімуму,
- точка мінімуму,  =20.
=20.
Оскільки 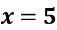 єдина точка мінімуму, то функція набуває в цій точці найменшого значення. Отже, сторони прямокутника дорівнюють 5 см і 5 см, тобто квадрат зі стороною 5 см.
єдина точка мінімуму, то функція набуває в цій точці найменшого значення. Отже, сторони прямокутника дорівнюють 5 см і 5 см, тобто квадрат зі стороною 5 см.
docx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку