Презентація за темою: "Точки екстремуму функції"
Про матеріал
Презентація створена як допомога до викладання нової теми. Використовувати можна під час карантину для самостійного вивчення, так і демонстрація під час конференції в ZOOM або Skype Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


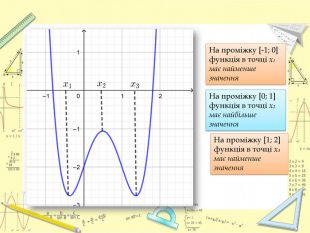
![На проміжку [-1; 0] функція в точці x₁ має найменше значення. На проміжку [0; 1] функція в точці x₂ має найбільше значення. На проміжку [1; 2] функція в точці x₃ має найменше значення На проміжку [-1; 0] функція в точці x₁ має найменше значення. На проміжку [0; 1] функція в точці x₂ має найбільше значення. На проміжку [1; 2] функція в точці x₃ має найменше значення](/uploads/files/580506/170371/183046_images/2.jpg)
![f(x₁) ≤ f(x) [ -1; 0]f( x₂) ≥ f(x) [0; 1]f(x₃) ≤ f(x) [1; 2] f(x₁) ≤ f(x) [ -1; 0]f( x₂) ≥ f(x) [0; 1]f(x₃) ≤ f(x) [1; 2]](/uploads/files/580506/170371/183046_images/3.jpg)





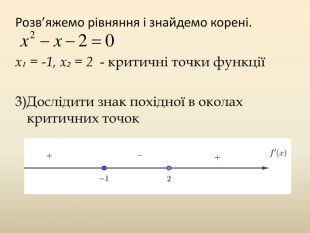
![х³ - 8 = 0;х³ = 8;х = 2.3)4) Проміжки зростання х є ( - ∞;0) і [2;+∞) спадання х є (0;2] х³ - 8 = 0;х³ = 8;х = 2.3)4) Проміжки зростання х є ( - ∞;0) і [2;+∞) спадання х є (0;2]](/uploads/files/580506/170371/183046_images/11.jpg)

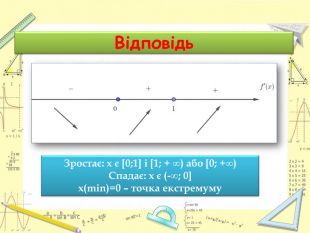
![Відповідь. Зростає: х є [0;1] і [1; + ∞) або [0; +∞)Спадає: х є (-∞; 0]х(min)=0 – точка екстремуму Відповідь. Зростає: х є [0;1] і [1; + ∞) або [0; +∞)Спадає: х є (-∞; 0]х(min)=0 – точка екстремуму](/uploads/files/580506/170371/183046_images/13.jpg)









-

Живора Татьяна
22.09.2023 в 21:27
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
4.0
-

Лебедева Юля
19.04.2023 в 11:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
13.03.2023 в 17:25
Все шикарно!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Харченко Ірина Вікторівна
17.04.2022 в 12:54
ДЯКУЮ!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гмиря Аліна
15.04.2022 в 13:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Семенюк Елена
19.02.2022 в 13:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Яворська Юлія Анатоліївна
30.03.2021 в 20:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кучера Наталія Василівна
09.03.2021 в 09:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Нижборська Наталія
11.06.2020 в 22:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків