Конспект уроку з теми:" Системи нерівностей з двома змінними." 10 клас, профіль
УРОК
Тема. Системи нерівностей з двома змінними . Розв’язування задач.
Мета:
дидактична – розвивати пізнавальну діяльність учнів, вдосконалювати вміння і навички розв’язувати нерівності і системи нерівностей різного рівня складності графічним способом;
методична - ознайомити з поняттям систем нерівностей з двома змінними, закріпити поняття нерівностей з двома змінними, вдосконалювати навички розв’язання задач за допомогою графічного способу розв’язання нерівностей;
виховна - виховувати в учнів позитивну мотивацію навчання, розвивати вміння встановлювати логічний зв'язок між прикладними задачами і їх математичними моделями для успішного розв’язання.
Тип уроку: засвоєння нових знань, умінь, навичок, закріплення основних понять з попередньої теми.
Учні повинні:
- закріпити поняття про нерівності з двома змінними ;
- засвоїти основні способи розв’язування систем нерівностей;
- здійснювати аналіз умови задачі для вибору більш вдалого способу її розв’язання;
- розв’язувати системи нерівностей різного рівня складності графічним способом.
Обладнання та матеріали: інтерактивна дошка, слайди.
І. Організаційний момент уроку (1-3 хв.)
Вступне слово вчителя.
- Сьогодні на уроці ми будемо закріплювати вже вивчені методи розв’язку нерівностей з двома змінними, повторимо графічний спосіб розв’язку нерівностей і будемо розвивати вміння розв’язувати задачі за допомогою нерівностей. Почнемо з перевірки домашнього завдання.
ІІ. Перевірка домашнього завдання ( 5-7хв.)
Фронтальна перевірка проходить у формі ігрового моменту(щоб заощадити час на цьому етапі уроку). Відповіді до завдань(разом з неправильними) представлені на дошці. Вчитель повідомляє учням, що всі відповіді були правильними, але випадково хтось переплутав картки і вивісив їх в довільному порядку. Треба поновити правильний порядок і знайти серед запропонованих карток ті, що відповідають домашнім вправам
Слайд 1
№345
1) 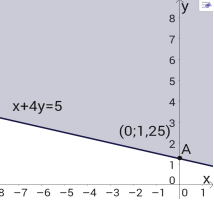 2)
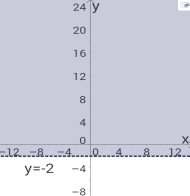
2) 
3)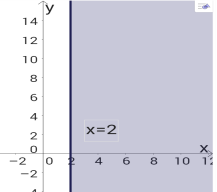 4)
4) 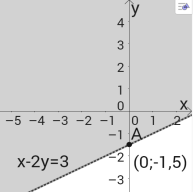
5)  Відповіді: 4) х – 2у > 3;1) х +4у
Відповіді: 4) х – 2у > 3;1) х +4у ![]() 5;2) у > -2;
5;2) у > -2;
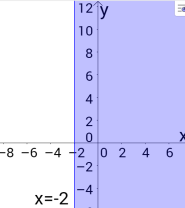
5).х ![]() -2.
-2.
Перевірка за малюнками на дошці. Для перевірки домашнього завдання на дошку проектується слайд 2
Слайд 2
№332(1), 335(1)
Коментар. ![]() =
= ![]() .
.
При у![]() 0 – без змін, при у<0 - симетрія відносно Ох.
0 – без змін, при у<0 - симетрія відносно Ох.
Коментар .х = ![]() ,
, 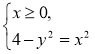
№348(1,3,5)
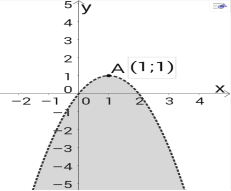
1) у < 2х-х2
Вершина параболи (1,1). Точка А(0;-1) належить графіку нерівності.
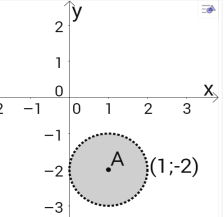
3) Коментар. (х-1)2+(у+2)2 ![]() 1. Рівняння кола з центром (1,-2) і радіусом 1
1. Рівняння кола з центром (1,-2) і радіусом 1
(х-1)2+(у+2)2 = 1.
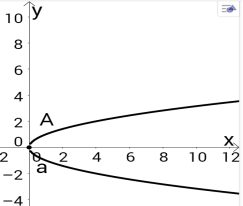
5) Коментар. ху < 2.
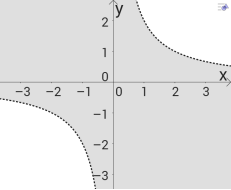 у =
у = ![]() - гіпербола ( І, ІІІ чв.). Перевіримо, чи належить точка А(2,2) графіку нерівності:
- гіпербола ( І, ІІІ чв.). Перевіримо, чи належить точка А(2,2) графіку нерівності:
2![]() 2 < 2- невірно, тому точка А не належить графіку. Точка В(1;-2) належить графіку нерівності, той частині площини, яка є розв’язком.
2 < 2- невірно, тому точка А не належить графіку. Точка В(1;-2) належить графіку нерівності, той частині площини, яка є розв’язком.
В ході перевірки задаються питання:
- Графіки яких функцій були представлені при розв’язку нерівностей?
- На яких малюнках представлені графіки функцій?
- Як за відомим графіком функції у = f(x) побудувати графіки нерівностей
у > f(x), у < f(x)?
4. Що є графіком нерівності х > a, x < a?
5. Що є графіком нерівності х2+ у2 < R2, х2+ у2 > R2?
6. Що називається графіком нерівності з двома змінними?
Далі учитель підводить підсумки.
Графіки нерівностей можна знайти за однією загальною схемою:
- Побудувати графік рівняння F(х, у) = 0, який розбиває координатну площину на декілька областей.
- У кожній області обираємо «пробні точки».
- За допомогою цих точок встановлюємо, які з областей належать шуканому графіку та об’єднуємо їх.
III. Формулювання мети і завдань уроку (5-7 хв.)
3.1 Мотивація навчальної діяльності учнів
Учням пропонується розв’язати задачу.
Задача . Зустрічаються дві команди шашкістів А і В. За умовами змагань кожен учасник однієї команди грає по одній партії з кожним учасником іншої команди. Загальна кількість майбутніх партій у 4 рази більша за кількість усіх гравців в обох командах. Однак через хворобу два гравці не змогли з’явитися на матч, у зв’язку з чим кількість усіх зіграних у матчі партій виявилося на 17 менше за передбачувану. Скільки гравців виступило в матчі за команду А, коли відомо, що в ній було менше гравців, ніж у команді В?
(колективно розв’язується)
Позначимо кількість гравців, що повинні були виступити відповідно за команди А і В, через m і n (n >m)
Очевидно, що планувалося зіграти т n партій. Перша умова задачі приводить до рівняння m n = 4( m + n).
Друге рівняння відразу записати не можна, оскільки невідомо, до яких команд належали захворілі гравці. Можливі три випадки:
1) якщо занедужали гравці команди А, то (m - 2) n = m n – 17;
2) якщо занедужали гравці команди В, то (n - 2) m = m n – 17;
3) якщо занедужало по одному гравцю з команд А і В, то
(m - 1) ( n - 1) = m n – 17.
Перший випадок дає 2n = 17, що неможливо, оскільки п — ціле число. Другий випадок також неможливий з цієї причини: 2m ≠ 17, у третьому випадку дістаємо систему:
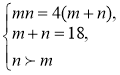 .
.
Звідси легко знаходимо m = 6, n = 12.
Відповідь. За команду А виступило 6 гравців.
Вчитель зазначає, що розв’язок зводить до складання системи рівнянь та нерівності, яку можна розв’язати графічно.
3.2 Актуалізація опорних знань учнів.
Графічне розв’язання системи: позначимо х = n, у = m
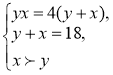 ,
, 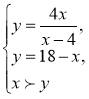
Графік першого рівняння – гіпербола, другого рівняння – пряма; нерівність показує ту частину площини, яка відповідає її розв’язкам. Точка А(12,6) є точкою перетину графіків рівнянь і задовольняє множині розв’язків нерівності ( див. рис.).
Слайд 3
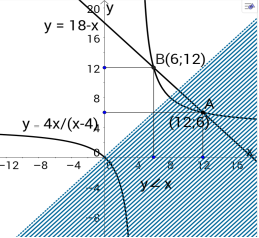 Можна побачити на малюнку, що э ще одна точка перетину графіків
Можна побачити на малюнку, що э ще одна точка перетину графіків
у = 18-х і у = 4х/(х-4), це точка (6,12). Але координати цієї точки не задовольняють нерівність у < х.
Вчитель задає питання:
- Як на вашу думку можна розв’язати графічно систему нерівностей з двома змінними?
- Що буде множиною розв’язків системи нерівностей в координатній площині?
Після обговорення пропонується практична робота в парах на графічне розв’язання систем.
ІV. Вивчення нового матеріалу (10-15хв.)
План вивчення нового матеріалу
1.Уявлення про системи нерівностей з двома змінними.
2. Прикладні задачі, що зводяться до складання систем нерівностей з двома змінними.
3. Розв'язок систем нерівностей з двома змінною графічним способом.
Приклад. Розв’язати нерівність: (х2+у2-4)(х2+у2-16) ![]() 0.
0.
Оскільки добуток дорівнює нулю тоді і тільки тоді, коли хоча б один із множників дорівнює нулю, то рівняння (х2+у2-4)(х2+у2-16)=0 буде задавати дві лінії х2+у2 = 4, х2+у2 = 16. Графіки рівнянь ділять площину на три частини. За допомогою “пробних” точок з’ясовуємо, що шукана нерівність виконується в кільці, яке обмежено двома колами з R=2 і R=4
( див. рис.3). Розв’язок нерівності зводиться до роз візку систем 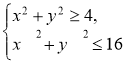 або
або 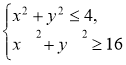
Розв’яжемо, наприклад, першу систему.
Алгоритм практичної роботи, яка пропонується на етапі побудови множини розв’язків системи нерівностей.
Рис. 1
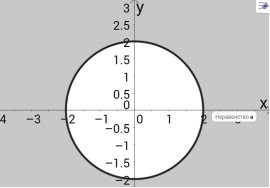 Один з учнів пари будує графік нерівності х2+у2
Один з учнів пари будує графік нерівності х2+у2![]() 4 на чистому папері з відповідним масштабом.
4 на чистому папері з відповідним масштабом.
Після аналізу умови будуємо графік рівняння х2+у2=4, для цього в кожного учня заготовлено папір у клітинку і за допомогою “пробних” точок з’ясовуємо область, яка є розв’язком нерівності х2+у2![]() 4 (заштриховуємо її зеленим кольором, рис. 1)
4 (заштриховуємо її зеленим кольором, рис. 1)
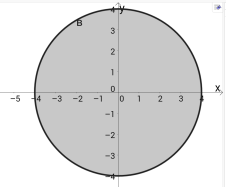
Другий учень будує графік нерівності х2+у2![]() 16 на прозорому папері з таким самим масштабом, що і у першого учня ( заштриховуємо червоним кольором, рис. 2).
16 на прозорому папері з таким самим масштабом, що і у першого учня ( заштриховуємо червоним кольором, рис. 2).
Рис.2
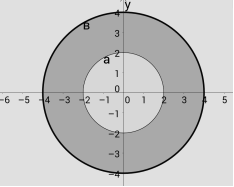
 Далі другому учню вчитель пропонує сумістити накладанням прозорий папір (рис.2) з фігурою (рис.1) першого учня і знайти перетин множин розв’язків двох нерівностей наочно – область перетину різних кольорів (рис.3).
Далі другому учню вчитель пропонує сумістити накладанням прозорий папір (рис.2) з фігурою (рис.1) першого учня і знайти перетин множин розв’язків двох нерівностей наочно – область перетину різних кольорів (рис.3).
Рис.3
 Вчитель робить висновки:
Вчитель робить висновки:
Розв'язати систему нерівностей з двома змінними— значить знайти множину всіх таких точок координатної площини, координати яких задовольняють одночасно всім нерівностям системи.
Отриману фігуру називають графіком системи нерівностей.
Аналогічно можна показати розв'язок систем нерівностей з трьома або більшою кількістю нерівностей.
Приклад. Розв’язати систему нерівностей 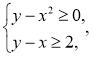
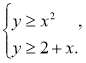
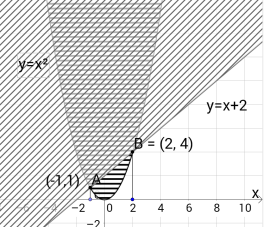
Розв’язки системи можна зображувати на координатній площині. Для цього слід побудувати графіки нерівностей, які складають систему, і знайти їх перетин. Графіком першої нерівності є фігура, показана на рисунку горизонтальною штриховкою. Графіком другої нерівності є півплощина, показана на рисунку штриховкою іншого напряму. Фігура, яка зображує розв’язки системи, позначена подвійною штриховкою.
V. Закріплення нових знань та вмінь учнів (7-10 хв.)
Приклад. Розв’язати систему нерівностей:
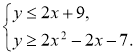
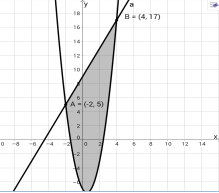
Рис. 4
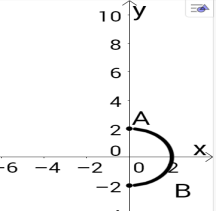
Приклад. Задайте за допомогою нерівностей область, яка зображена на малюнку.
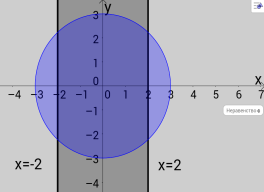
Відповідь. 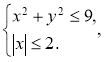
Вчитель підводить підсумок уроку.
VІ. Домашнє завдання (заздалегідь записано на дошці).
Вивчити §17, (підручник. А.Г. Мерзляк, Алгебра 10, проф. рівень,
№ 354(2), №355(5),№356(2), №358(2).
1


про публікацію авторської розробки
Додати розробку
