Конспект уроку з алгебри 9 клас на тему: Сума n перших членів арифметичної прогресії.
Тема: Сума п перших членів арифметичної прогресії.
Мета: вивести формулу Sn для арифметичної прогресії; навчити обчислювати Sn; знаходити раціональні способи розв'язування задач: ознайомити учнів з історією математики; розвивати кмітливість; виховувати елементи логічного мислення.
Тим уроку: комбінований.
Хід уроку.
- Організаційний момент.
- Перевірка домашнього завдання.
- До дошки викликати двох учнів для розв’язування завдань на карточках.
Картка № 1. Знайти ![]() , якщо
, якщо ![]() = 3; d = 5.
= 3; d = 5.
Картка № 2. Знайти а1, якщо ![]() = 18; d = - 2,
= 18; d = - 2,
- З усіма іншими учнями перевіряється правильність виконання домашніх завдань.
- Математичний марафон.
- Які бувають послідовності?
- Як задати послідовність?
- Які є способи задання послідовності?
- Яка послідовність називається арифметичною прогресією?
- Як задати арифметичну прогресію?
- Як позначається різниця арифметичної прогресії?
- Як знайти n - й член арифметичної прогресії?
- Яку властивість має арифметична прогресія?
ІІІ. Мотивація навчальної діяльності.
Епізод із біографії вченого - математика, який певним чином пов’язаний з деякими задачами.
Спробуйте встановити цей зв’язок. Він і буде темою нашого подальшого вивчення.
(Демонструється портрет К. Гаусса).
У 7 років Карл Гаусс пішов до школи. Якось учитель дав учням досить складне завдання: додати всі числа від 1 до 100. Учитель вважав, що учні досить довго шукатимуть відповідь. Але через кілька хвилин Карл написав на своїй грифельній дошці відповідь. Коли вчитель проглянув розв’язання, то побачив, що маленький Гаусс винайшов спосіб скороченого знаходження суми членів арифметичної прогресії.
- Як же ти підрахував? - запитав учитель.
- Дуже просто, - відповів хлопчик.
- Я додав 1 і 100, одержав 101. Потім додав 2 і 99, теж одержав 101 і так 50 доданків по 101 кожний. Помножив 101 на 50. Одержав 5050.
Здивований вчитель зрозумів, що зустрів найобдарованішого учня у своєму житті. Отже, К. Гаусс обчислив суму 100 перших членів арифметичної прогресії. А саме суму потрібно знайти в багатьох історичних задачах.
Причому для знаходження цих сум математики давно не користувалися безпосереднім додаванням для цього вони застосовували формули.
Сьогодні на уроці ми виведемо формулу суми членів арифметичної прогресії та навчимося її застосовувати в різних випадках.
IV. Вивчення нового матеріалу.
Запишемо суму, яку успішно обчислив юний Гаусс.
S = 1 + 2 + 3+ ... +99 + 100,
S = 100 + 99 + 98 + ... + 2 +1
2 S = 101 * 100,
S = 101 * 100/2 = 5050.
З допомогою аналогічних міркувань можна знайти суму перших членів будь - якої арифметичної прогресії. (Це може зробити один із учнів).
Sn = ![]()
Sn = ![]()
2 Sn = ![]()
Sn = ![]()
Що потрібно знати, щоб скористатися цією формулою?
Ця формула може виявитися не зовсім зручною, якщо невідомий член ![]() а тому доведеться спочатку обчислювати його. Спробуйте перетворити цю формулу так, щоб її можа було використовувати, знаючи a1 i d.
а тому доведеться спочатку обчислювати його. Спробуйте перетворити цю формулу так, щоб її можа було використовувати, знаючи a1 i d.
![]() .
.
- Тренувальні вправи.
-
Знайдіть суму 60 перших членів арифметичної прогресії (аn), якщо
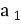 = 3;
= 3; 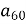 = 57. (1800).
= 57. (1800).
- Знайти Sn
-
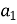 = 3; d = 2; n = 32;
= 3; d = 2; n = 32;
-
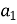 = -5; d = - 7; n = 12;
= -5; d = - 7; n = 12;
-
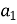 = 8; d = 0; n = 50.
= 8; d = 0; n = 50.
- Знайдіть суму перших сорока членів арифметичної прогресії:
а) 2, 7, 12, 17,...;
б) -3, -6, -9, ....
- Людям, які копають криницю, обіцяють за перший метр заплатити 30 грн, а за кожний наступний на 20 грн, більше, ніж за попередній. Скільки вони одержать за копання 12 - метрової криниці?
- Знайдіть суму 50, ста, n перших членів послідовності (аn), якщо
аn = 4n + 2 .
Перша задача розв’язується біля дошки 2 - ма способами. Який спосіб раціональний у даному випадку?
Учні самостійно закінчують це завдання.
- Підсумок уроку.
- Домашнє завдання.
§ 20. №599, № 603, №611.


про публікацію авторської розробки
Додати розробку
