Рівняння з двома змінними
конспект уроку та презентація уроку "Рівняння з двома змінними"
В даній презентації детально розглядається вигляд графіка лінійного рівняння з двома змінними (зокрема, особливих його видів) та алгоритм побудови його на координатній площині.
Тема уроку: Рівняння з двома змінними.
Мета уроку: Ввести поняття рівняння з двома змінними, його степеня. Домогтися засвоєння учнями змісту означення рівняння з двома змінними Розвивати в учнів аналітичне та алгоритмічне мислення. Виховувати в учнів культуру та інтерес до вивчення математики.
Тип уроку: комбынований
Епіграф уроку:
Не достатньо мати лише добрий розум,
Головне – це раціонально застосовувати його.
Хід уроку:
І. Організаційна частина.
Перевірка готовності учнів до уроку.
ІІ. Аналіз контрольної роботи


№10.17(10-12)
ІІІ. Актуалізація опорних знань.


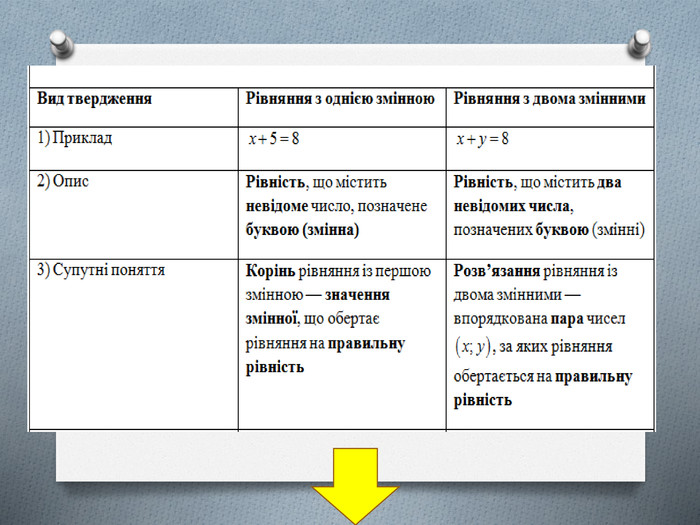
1. Повторити відомості про лінійні рівняння з однією змінною та двома змінними у вигляді порівняльної таблиці 1.
|
Таблиця 1 |
|||
|
Вид твердження |
Рівняння з однією змінною |
Рівняння з двома змінними |
|
|
1) Приклад |
х + 5 = 8 |
х + у = 8 |
|
|
2) Опис |
Рівність, що містить невідоме число, позначене буквою (змінна) |
Рівність, що містить два невідомих числа, позначених буквою (змінні) |
|
|
3) Супутні поняття |
Корінь рівняння із однією змінною − значення змінної, що перетворює рівняння на правильну рівність |
Розв’язок рівняння із двома змін-ними − впорядкована пара чисел (х; у), за яких рівняння перетво-рюється на правильну рівність |
|
|
4) Рівносильні |
рівняння з однією змінною − мають однакові корені або взагалі не мають коренів |
рівняння з двома змінними − мають одні й ті самі розв’язки або обидва не мають розв’язків |
|
|
5) Властивості рівносильних рівнянь |
1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. |
||
|
6) Графік |
? |
Фігура, що складається з точок (х; у), таких, що їх корди-нати − розв’язки рівняння |
|
ІІІ. Мотивація учбової діяльності.
Розв’язування алгебраїчних та геометричних задач часто призводить до необхідності розв’язувати системи рівнянь з двома змінними. Тому сьогодні ми повинні розглянути поняття з двома змінними.
ІV. Засвоєння нових знань.
Прирівняємо розглянуті многочлени до нуля, отримаємо:
а) 2х − 5у + 2 = 0;
б) х2 − 6ху − 4 = 0;
в) ху2 + 7х2 − 4ху2 + 2 = 0;
г) −3ху2 + 7х2 + 2 = 0;
д) 4х2у2 + 3ху2 − х2 + 4 = 0.
В результаті отримали рівняння з двома змінними, які можна представити у вигляді F (x; y) = 0.
Степінь цілого рівняння з двома змінними F (x; y) = 0 визначається як степінь многочлена F (x; y), якщо він зведений до стандартного вигляду.
(Учні визначають степінь кожного рівняння).
а) рівняння першого степеня: ах + bу + с = 0, ( а2 + b2 ≠ 0);
б) рівняння другого степеня: ах2 + bу2 + сху + dх + еу + f = 0, ( а2 + b2 + с2 ≠ 0);
Розв’язком рівняння з двома змінними х і у є впорядкована пара (x; y), яка перетворює рівняння на правильну рівність.
Усно:







Завдання підвищеної складності
№12.1
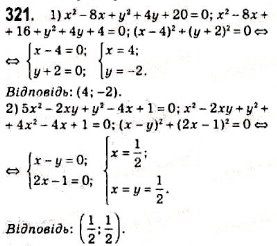
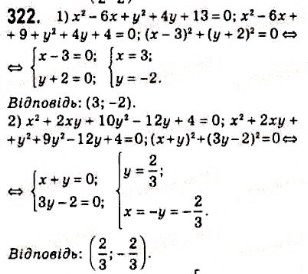
VІ. Підсумок уроку.

VІІ. Домашнє завдання.
П.12
1.Чи є розв'язком рівняння х2 + у = 10 пари чисел:
- (3;1);
- (- 2;6);
- (1; - 3).
2.Виразіть одну змінну через іншу і знайдіть два будь – які розв'язки рівняння:
- х2 – у + 3 = 0;
- х + 3у + ху = 2;
- у = х2 +3;
№12.2*


про публікацію авторської розробки
Додати розробку