Конспект уроку з алгебри для 9 класу на тему: "Узагальнення знань по темі "Арифметична прогресія".

Урок з алгебри для 9 класу

Тема: узагальнення знань по темі «Арифметична прогресія».

Мета: 1. Узагальнити та систематизувати знання про арифметичну прогресію, здобуті на попередніх уроках; продовжувати формувати в учнів уміння та навички застосовувати здобуті знання при розв’язуванні задач і вправ, в тому числі практичного змісту.

2. Розвивати логічне мислення, обчислювальні навички, пізнавальну активність, увагу, навички само- та взаємоконтролю, швидкість реакції.

3. Виховувати культуру математичних записів та мови; інтерес до предмету, наполегливість і старанність у праці, почуття поваги, доброзичливості та товаристкості.

Тип уроку: урок закріплення знань.

Обладнання уроку: епіграфи до уроку; індивідуальні різнорівневі картки для роботи біля дошки та в парі; картки для усного рахунку; картки для групової роботи; «поле чудес» для  розгадування девізу уроку; «ключ» до «поля чудес»; індивідуальні різнорівневі картки для самостійної роботи.

Хід уроку:

Біля дошки висять епіграфи до уроку:

1. Недостатньо лише мати добрий розум, головне – це раціонально застосовувати його.

Р.Декарт

2. Математика безмежно раціональна, як світ, і присутня, міститься в усьому.

М.П.Єругін

1. Організаційна частина (вступне слово вчителя).

Сьогодні у нас заключний урок по темі «Арифметична прогресія». Тому за мету сьогоднішнього уроку поставимо: узагальнити та систематизувати свої знання про арифметичну прогресію в процесі повторення теоретичного матеріалу та розв’язування різних видів вправ.

2. Перевірка домашнього завдання (якщо в учнів є запитання, то вчитель дає відповіді на них; якщо запитань немає, то наголошує, що домашнє завдання буде частково перевірено протягом уроку, а в кінці уроку буде запропонована різнорівнева самостійна робота, до якої будуть включені деякі вправи, подібні до домашніх).

3. Теоретична розминка.

1. Сформулювати означення арифметичної прогресії. Навести приклади.

2. Що називається різницею арифметичної прогресії? Як її знайти?

3. Яка арифметична прогресія називається зростаючою (спадною)?

4. Як може бути задана арифметична прогресія?

5. Задайте арифметичну прогресію рекурентною формулою.

6. Задайте арифметичну прогресію формулою n-того члена.

7. Яка з формул більш раціональна у використанні?

8. Сформулюйте основну властивість арифметичної прогресії.

9. За якою формулою можна знайти суму n перших членів арифметичної прогресії?

10. Яку властивість мають члени скінченної прогресії, однаково віддалені від її кінців?

4. Робота в парі, індивідуально біля дошки і паралельно усний рахунок.

Повторивши коротенько теоретичний матеріал, переходимо до розв’язування вправ. Але в процесі розв’язування вправ нам необхідно розшифрувати народну мудрість, яка буде девізом сьогоднішнього уроку. Ця мудрість зашифрована на «полі чудес». Номери літер будуть відповідати номерам карток, які ми розв’яжемо сьогодні. А «ключ» до розшифрування знаходиться в таблиці; правильна відповідь покаже  на відповідну літеру (див.додаток).

Картки різнорівневі: жовтого кольору – середній рівень, синього – достатній рівень, червоного – високий рівень.

Але отримані картки – це не кінцеві ваші бали. Вони можуть бути підвищені в процесі роботи на уроці.

 а) робота в парі (на місцях);

 Картка №4 – 2 шт. жовтого кольору.

 Задача. Послідовність – арифметична прогресія, задана формулою . Чи буде сума її тридцяти перших членів дорівнювати 1020?

 Відповідь: так. н 

Картка №10 – 2 шт. синього кольору.

Задача. Між числами -5 і 19 вставте 5 таких чисел, щоб вони разом із даними утворили арифметичну прогресію. Який її середній член?

Відповідь: -5; -1; 3; 7; 11; 15; 19.

                    7. к 

Картка №13 – 2 шт. синього кольору.

Задача. В арифметичній прогресії перший член дорівнює 5, різниця  (-0,5). Для яких членів арифметичної прогресії виконується умова: ? Вказати номер першого такого члена.

Відповідь: ; б 

Картка №5 – 2 шт. червоного кольору.

Задача. Чи буде сума всіх двоцифрових чисел, які при діленні на 3 дають в остачі 2, дорівнювати 1648?

Відповідь: так. н 

б) індивідуальна робота біля дошки

Картка 12 – 1 шт. жовтого кольору (задача-жарт).

Задача. Тарас у січні отримав 5 двійок, а кожен наступний місяць на 4 двійки більше, ніж за попередній. Скільки двійок отримав Тарас до кінця навчального року?

Відповідь: 65. р 

Картка №7 – 1 шт. синього кольору.

Задача. Сума другого і четвертого членів арифметичної прогресії 16, а добуток першого і п’ятого 28. Знайти різницю та перший член арифметичної прогресії.

Відповідь: 3; 2 або -3; 14.  ц 

Картка №6 – 1 шт. червоного кольору.

Задача. Розв’язати рівняння: .

Відповідь: 10; -20,5.  я 

в) усний рахунок (із класом).

1. Чи є вказана послідовність арифметичною прогресією:

1. 3; 9; 27; …
2. 7; 3,5; 0; -3,5; …
3. ; ; ; …
4. ; ; ; …

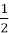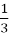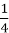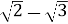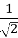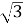2. Дано арифметичну прогресію: 2; 4; 6; … Усі її члени збільшено в 2 рази. Чи  утворюють знайдені числа арифметичну прогресію?

3. Дано арифметичну прогресію: 2; 4; 6; … Усі її члени збільшено на 20%. Чи утворюють знайдені числа арифметичну прогресію?

4. Різниця арифметичної прогресії дорівнює 5. Чому дорівнює різниця арифметичної прогресії, яку записано в зворотному напрямку?

5. Дев’ятий член арифметичної прогресії 18, а одинадцятий – 22. Чому дорівнює її десятий член?

6. Чи може сума скінченного числа членів арифметичної прогресії дорівнювати нулю?

7. Журнал складається із 16 вкладених один в одного подвійних аркушів. На якому подвійному аркуші сума чисел, якими пронумеровані сторінки, буде найбільшою (однакова)?

 5. Колективне розв’язування вправ.

Картка №2 – 1 шт. червоного кольору (задача-жарт).

Задача. Турист, піднімаючись на гору, за першу годину досяг висоти 800 м., а його восьмикілограмовий рюкзак щогодини стає легшим на 1 кг. Чи одночасно відбудуться дві події: спорожніє рюкзак та турист підніметься на висоту 5700 м., якщо за кожну наступну годину він піднімався на 25 м. менше, ніж за попередню?

Відповідь: так.  н 

Картка №9 – 1 шт. червоного кольору.

Задача. Чи утворять числа виду: ; ; , де арифметичну прогресію?

Відповідь: ні.  с 

(Вказівка: розв’язати рівняння: .)

6. Робота групами (група дівчат та хлопців).

Картка №3 – 1 шт. синього кольору (задача-жарт).

Задача. За довгу безсонну ніч Марія Іванівна так наслухалася бою годинника, що вирішила його комусь подарувати. Спочатку 11 ударів, потім 12, …, останні удари, які вона почула перед сном були о 6 год.ранку. Скільки ударів годинника примусили Марію Іванівну прийняти мудре рішення?

Відповідь: 44.  а 

Картка №1 – 1 шт. синього кольору.

Задача. Якась людина має багато коней і всім їм  різна ціна. Найгірший кінь коштує 4 золотих, а найкращий 55 золотих, і ціна піднімається від одного коня до другого весь час на 3 золотих. Скільки ж усього було коней?

Відповідь: 18.  з 

7. Екскурсія в історію.

Оскільки можливості нашого уроку обмежені, тому, щоб відкрити останні дві літери, давайте згадаємо трохи історію. Ці літери – це початкові літери імен вчених, які вам добре відомі, які ми неодноразово згадували, адже ці вчені внесли також свій вклад у розвиток вчення про прогресії. Як звати вчених – видатних математиків?  (Евклід, Архімед).

Отже, девіз уроку «Знання – це скарб». Нехай цей вислів буде девізом не тільки сьогоднішнього уроку або вашої навчальної діяльності, а й всього життя.

8. Різнорівнева самостійна робота з наступною перевіркою.

(Учні на вибір вибирають одне з трьох запропонованих завдань: завдання №1 – середнього рівня, завдання №2 – достатнього рівня, завдання №3 – високого рівня.)

Після виконання самостійної роботи учні обмінюються зошитами, по одному учню коментують розв’язання, решта учнів перевіряють і виставляють один одному оцінки).

І варіант

1. Визначити число членів в арифметичної прогресії, якщо: , , .

Відповідь: 7.

2. (Задача із «Арифметики» Л.П.Магницького). Деякий купець мав 14 срібних чашок, причому кожна з них за масою перевищувала попередню  на 4 г., а остання чашка важила 59 г. Скільки важать всі чашки?

Відповідь: 462 г.

3. У театрі 10 рядів. На першому ряді 100 місць, а в кожному наступному на 20 місць більше, ніж у попередньому. На виставу продано 1683 квитки. Скільки вільних місць залишиться у театрі?

Відповідь: 217.

ІІ варіант

1. Визначити число членів арифметичної прогресії, якщо: , , .

Відповідь: 11.

2. Скільки грошей вторгував продавець за 10 днів, якщо за кожен день він торгував на 12 золотих більше, ніж за попередній, а за десятий день вторгував 148 золотих?

Відповідь: 940.

3. У позику безпроцентно  взято 8500 золотих. Яку суму грошей залишилося віддати, якщо за перший із семи років віддано 500 золотих, а за кожний наступний – на 200 золотих більше, ніж за попередній?

Відповідь: 800 золотих.

9. Підсумок уроку (методом «незакінчене речення»).

На сьогоднішньому уроці ми:

1. повторили…
2. навчилися…
3. я знаю, що…
4. я знаю, як…
5. я знаю чому потрібно…

10. Домашнє завдання (за підручником з алгебри для 9 класу загальноосвітніх навчальних закладів, автори Мерзляк А.Г., Полонський В.Б., Якір М.С.).

Повторити п.16, 17.

Розв’язати: середній рівень - №20.78; 20.80; 20.84(1), достатній рівень - №20.81; 20.83; 20.89, високий рівень - №20.85; 20.91; 20.94.

На 12 балів:

 Задача. Перші три члени зростаючої арифметичної прогресії при деякому значенні n можуть бути задані відповідно виразами: ; ; . На скільки сума 43 перших членів цієї прогресії більша, ніж сума 40 її перших членів?

 

 

 

 

 

 

 

 

Додаток

«Поле чудес»

 

1	2	3	4	5	6		7	8		9	10	11	12	13
З	Н	А	Н	Н	Я	-	Ц	Е		С	К	А	Р	Б

 

«Ключ» до «поля чудес»

А	Б	В	Е	З	К	М	Н
44	11	3; -2; 16; 14	5; -8; 13; 4	18	7	-5; 12	ТАК
О	Я	Р	С	Т	Х	Ц	Ч
37	10; -20,5	65	НІ	13; -6	15	3; 2; -3; 14	81