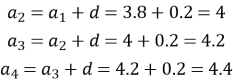Конспект уроку з алгебри на тему: "Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії"
Конспект уроку математики в 9 класі, студентки групи МІЕ17Б Чудної Олени
Тема: Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії.
Мета:
-
Навчальна:
- навчити формувати означення арифметичної прогресії;
- навчити формувати поняття n-го члена арифметичної прогресії;
- навчити формулі n-го члена арифметичної прогресії.
-
Виховна:
- виховувати інтерес до знань;
- виховувати наполегливість.
- Розвиваюча:
- розвивати вміння аналізувати, систематизувати, теоретичні відомості;
- розвивати мислення, пам’ять, увагу.
Тривалість уроку: 45 хвилин.
Тип уроку: урок засвоєння нових знань.
План уроку
- Організаційний момент (3 хвилини)
- Перевірка домашнього завдання (4 хвилин)
- Актуалізація опорних знань та мотивація навчальної діяльності учнів (8 хвилин)
- Пояснення нового матеріалу (25 хвилин)
- Підсумок уроку (3 хвилини)
- Постановка домашнього завдання (2 хвилини)
Хід уроку
І. Організаційний момент.
Привітання вчителя. Перевірка готовності учнів до уроку. Перевірка присутніх на уроці (відмітити в журналі).
ІІ. Перевірка домашнього завдання.
Підручник: Алгебра: підруч. для 9-го кл. загальноосвіт. навч. закл./ О.С. Істер. – Київ: Генеза, 2017. – 264 с.
Вчитель заздалегідь записує дані номери на дошці, а на уроці діти звіряють своє д/з з записами на дошці.
№677 (1-2)
Послідовність задано формулою ![]() Які із чисел є членами цієї послідовності? Для чисел, що є членами послідовності, укажіть їх номери.
Які із чисел є членами цієї послідовності? Для чисел, що є членами послідовності, укажіть їх номери.
- 69
![]()
![]()
![]()
![]()
Оскільки n – натуральне число, то ![]()
- 68
![]()
![]()
![]()
Рівняння не має натуральних коренів, отже число 68 не є членом послідовності.
№687
- Запишіть числову послідовність, що містить десять членів, у якої перший член дорівнює 2, а кожний наступний – на 3 більший за попередній.
2, 5, 8, 11, 14, 17, 20, 23, 26, 29.
- Запишіть формулу n-го члена цієї послідовності.
![]()
№688
Знайдіть закономірність і продовжте ряд чисел, записавши чотири наступних числа ряду:
- 42, 45, 48, 51, 54, 57, 60, 63.
- 6, 1, -4, -9, -14, -19, -24, -29.
- 15, 0, -15, -30, -45, -60, -75, -90.
- -13, -9, -5, -1, 3, 7, 11, 15.
ІІІ. Актуалізація опорних знань та мотивація навчальної діяльності учнів
На попередньому уроці ми з вами з’ясували, що таке послідовність і що вона повсюди нас супроводжує: на нотному стані, на штрих-коді і навіть наші пальці рук утворюють послідовність. Та чи знали ви, що існують й особливі послідовності? (відповіді учнів). Дійсно в математиці є цікаві послідовності, однією з них є – арифметична прогресія, з нею ми сьогодні й познайомимося.
«Прогресія – це рух вперед», так і ми рухаємось вперед у вивченні математичних понять.
Давайте пригадаємо:
- Що таке числова послідовність? (функція, задана на множині всіх натуральних чисел або на множині перших n натуральних чисел).
- А які ж бувають послідовності? (скінченні, нескінченні, зростаючі, спадні). Добре.
-
А якими можуть бути члени послідовності відносно
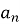 ? (наступний -
? (наступний - 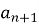 , попередній
, попередній 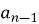 ).
).
ІV. Вивчення нового матеріалу.
Отож, як ви вже зрозуміли тема сьогоднішнього уроку: «Арифметична прогресія та її властивості».
Давайте ми з вами розглянемо дві послідовності чисел і з’ясуємо, що є в них спільного.
- 2; 4; 6; 8; 10; … (кожен член цієї послідовності, починаючи з другого, можна отримати, додавши до попереднього члена число 2);
- 9; 6; 3; 0; -3; …(кожен член цієї послідовності, починаючи з другого, можна отримати, віднявши від попереднього члена число 3 або додавши до попереднього члена число -3);
Ми можемо з вами помітити, що в цих послідовностях кожен член, починаючи з другого можна отримати додаванням до попереднього члена одного й того ж самого числа. Такі послідовності називаються арифметичними прогресіями. Спробуйте сформулювати означення арифметичної прогресії.
Арифметичною прогресією називають послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число.(під запис)
Це стале число для даної послідовності називають різницею арифметичної прогресії і позначають d. (під запис)
Якщо d > 0, то арифметична прогресія зростаюча, якщо ж d < 0, то прогресію називають спадною, при d = 0, прогресія є сталою. (під запис)
Тепер давайте разом з вами запишемо означення прогресії рекурентною формулою: ![]() Звідси можна знайти й d.
Звідси можна знайти й d.
Приклади (Які ці прогресії? зростаюча, спадна, стала).
- Прогресія 10; 15; 20; 25… є зростаючою, тому що d = 5;
- Прогресія 30; 26; 22; 18… є спадною, тому що d = -4;
- Прогресія 5; 5; 5; 5;… є сталою, тому що d = 0.
- Якими є послідовності? ( зростаюча, спадна, стала)
- Від чого це залежить? (від d)
Тепер давайте з вами знайдемо перших 4 члени арифметичної прогресії, якщо нам відомо, що ![]() , а d = 2.
, а d = 2.
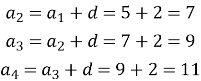
Це було просто, але давайте з вами уявимо, якби завдання вимагало б знайти ![]() чи
чи ![]() , ми б витратили багато часу, тому існує формула для знаходження n-го члена прогресії. Давайте спробуємо її вивести. Ми вже з вами знаємо, що:
, ми б витратили багато часу, тому існує формула для знаходження n-го члена прогресії. Давайте спробуємо її вивести. Ми вже з вами знаємо, що:
![]()
тоді далі,
![]()
![]()
![]()
Отож ми з вами бачимо певну закономірність: відповідний член прогресії отримують додаванням до першого її члена ![]() різниці
різниці![]() , помноженої на число менше на 1 від порядкового номера шуканого члена.
, помноженої на число менше на 1 від порядкового номера шуканого члена.
-
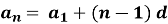 (під запис)
(під запис)
Тепер давайте, використовуючи виведену формулу, розв’яжемо приклади.
Приклад 1.
Вчитель викликає учня до дошки.
Знайти шостий член арифметичної прогресії, якщо відомо, що ![]()
![]() .
.
Розв’язання
![]()
Відповідь: 38
Приклад 2.
Вчитель викликає учня до дошки.
Знайти перший член арифметичної прогресії, якщо нам відомо, що ![]() , а
, а ![]() .
.
Розв’язання
![]()
![]()
Відповідь: 14
Приклад 3.
Вчитель викликає учня до дошки.
Знайдіть три наступні члени арифметичної прогресії 4,2; 3,8; 3,4;…
Розв’язання
![]()
Знайдемо різницю: ![]()
![]()
![]()
![]()
Молодці. Тепер до вас таке питання: як ви гадаєте, чому прогресія, яку ми з вами розглядаємо називається саме арифметичною? (відповіді учнів).
Арифметична прогресія має цікаву властивість: будь-який член арифметичної прогресії дорівнює середньому арифметичному його попереднього й наступного членів. Запишемо це формулою:
![]() (під запис)
(під запис)
Ця властивість називається характеристичною і саме через неї прогресія називається арифметичною.
Приклад 4.
Вчитель викликає 3 учнів до дошки.
За допомогою характеристичної властивості перевірити чи числова послідовність є арифметичною прогресією: 2, 5, 8, 11, 15, 18, 21…
Розв’язання
![]()
![]()
![]()
Отже, дана послідовність не є арифметичною прогресією.
V. Підсумок уроку.
Сподіваюсь ви дізналися багато нового. Давайте тепер підіб’ємо підсумки нашої роботи.
- Що називають арифметичною прогресією? (послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число).
- Від чого залежить, що арифметична прогресія зростає, спадає, є сталою? (Від її різниці).
- При якому d арифметична прогресія зростає?(d>0) Спадає?(d<0) Є сталою?(d=0).
-
Як виглядає формула n-го члена прогресії?
 .
.
- Про що говорить характеристична властивість арифметичної прогресії? (будь-який член арифметичної прогресії дорівнює середньому арифметичному його попереднього й наступного членів).
Виставлення оцінок за урок.
VІ. Постановка домашнього завдання.
Прочитати §16 підручника, вивчити конспект, №693,695, 697 (1,3) (Алгебра: підруч. для 9-го кл. загальноосвіт. навч. закл./ О.С. Істер. – Київ: Генеза, 2017. – 264 с.)
№693
Запишіть чотири перших члени арифметичної прогресії ![]() різниця якої дорівнює d.
різниця якої дорівнює d.
Розв’язання
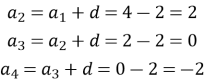
№695
Знайдіть чотири наступних члени арифметичної прогресії 5,7; 6,1; 6,5…
Розв’язання
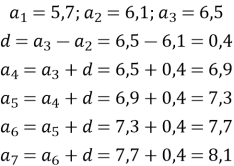
№697 (1,3)
В арифметичній прогресії ![]() Знайдіть:
Знайдіть:
3) ![]()


про публікацію авторської розробки
Додати розробку