Конспект уроку з геометрії для 9 класу на тему: "Додавання та віднімання векторів"

Тема уроку.Додавання та віднімання векторів.

Тип уроку: застосування знань і вмінь

Мета уроку :

Навчальна :удосконалити вміння розв’язувати задачі на дії з векторами, що задані координатами із залученням максимального числа завдань  різного рівня складності.

Розвивальна: Розвиток уваги, підвищення здібності до зосередження, креативних здібностей;

Розвиток  в учнів самостійності в знаходженні правильного вибору.

Розвиток математичного мислення, винахідливості, кмітливості, пам'яті.

Розширення кругозору.

Виховна:

Виховання шанобливого відношення один до одного і уміння колективне працювати.

Формування  в учнів пізнавального інтересу до математики.

 

Хід уроку

І. Організаційна частина.

Учням роздаються картки з побажаннями : високих балів, гарного настою , добрих знань,  успіхів у виконанні завдань ,  легких завдань , гарної оцінки

ІІ. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та від­повісти на запитання, які виникли в учнів під час його вико­нання.

На сьогоднішньому  уроці   я запрошую вас на   «Математичну біржу»

Біржа (нім. Börse, від пізньолат. bursa — гаманець) — організований торговельний майданчик, на якому відбувається гуртова торгівля товарами або цінними паперами у вигляді стандартизованих біржових угод. На біржі укладаються угоди по біржових товарах, в результаті чого утворюється динаміка ціни тільки під впливом ринкового попиту та пропозиції, що дає змогу орієнтуватися учасникам ринку та прогнозувати хід торгів в майбутньому.

Залежно від активів якими торгує біржа, їх поділяють на:

• товарні
• фондові
• валютні
• ф'ючерсні
• універсальні
• Товарна біржа — гуртовий, регулярно чинний ринок, де відбувається торгівля товарами за зразками або стандартами, в яких вказано перелік необхідних ознак (якість, сортність тощо).
• Фо́ндова бі́ржа — організаційно оформлений, постійно діючий ринок, на якому здійснюється торгівля цінними паперами; акціонерне товариство, яке зосереджує попит і пропозицію цінних паперів, сприяє формуванню їх біржового курсу та здійснює свою діяльність відповідно до чинного законодавства, статуту і правил фондової біржі.
• Валютна біржа — установа, в якій на підставі чинного законодавства здійснюється регулярна й упорядкована торгівля іноземною валютою відповідно до попиту і пропозиції.

 Сьогодні ви будете учасниками фондової біржі , та матимете змогу придбати акції вартість 1, 2 та 3 бали , які зможете в кінці уроку поміняти на оцінку за сьогоднішній урок.

ІІІ. Розв’язування вправ

1. Гра «Математичне доміно»

\ учитель готує набір карток двох кольорів. На одних записується початок речення, на інших його закінчення \

Наприклад:

Початок речення	Закінчення речення
Вектори називаються рівними …	Якщо вони співнапрямлені і мають рівні довжини
Два ненульових вектори називаються колінеарними…..	Якщо вони паралельні  або лежать на одній прямій
Щоб задати вектор…	Достатньо вказати його початок і кінець.
Два вектори називають протилежними векторами….	Якщо вони мають рівні модулі, але протилежні напрями.
Співнапрямленими векторами називають колінеарні вектори…	Якщо вони мають однаковий напрямок.
Нуль-вектором називають вектор…	Якщо його початок і кінець співпадають.
Довжиною вектора називають…	Відстань між його початком і кінцем.
Довжина нуль-вектора….	Дорівнює нулю.
Довжина і напрям вектора не залежать від…	Розміщення його початку в системі координат
Вектори рівні…	Коли їх відповідні координати рівні.
Вектори колінеарні…	Коли їх відповідні координати пропорційні

\ Кожній групі учнів роздається доміно, яке необхідно скласти у відповідності:  початок речення – кінець \

За правильне виконання одного завдання учень отримує 1 бал.

2.Інтерактивна вправа « НЕ ХОЧУ ХВАЛИТИСЯ, АЛЕ Я……»

( вправа застосовується під час повторення, узагальнення та систематизації знань )

• Найкраще засвоїв ….
• Добре знаю……
• Добре вмію…..
• Найкраще мені вдається…..
• Вмію розв’язувати….
• Вмію знаходити….
• Дані слова підказки висвітлюються на дошці чи на екрані \

 

• Які вектори називають колінеарними
• Які вектори називають співнапрямленими
• Протилежно напрямленими
• Рівними
• Протилежними
• Що називають довжиною вектора, або модулем
• Як встановити рівність векторів
• Додавати та віднімати вектори
• Знаходити  координати вектора

 

 

 1.Завдання з теми « Додавання та віднімання векторів»

Дано два вектори:(1; 5), (2; -1); 

Знайдіть: координати вектора:  2; -3; + ;   – ; 3 + 4.

           2.  Завдання з теми: «Координати вектора»

Знайти координати векторів : і ,

 якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)

 

           3. Завдання з теми: «Довжина вектора»

Знайдіть |2|, якщо (1; 2).

 

            4. «Колінеарні вектори»

Визначте, чи колінеарні вектори: а) (2; 3) і (-4; 6);         б) (1; 3) і (-3; -9).

 

             5. «Співнапрямлені вектори»

Доведіть, що вектори (1; 2) і (0,5; 1) однаково напрямлені

 

            6. Завдання з теми: «Протилежно напрямлені вектори»

Доведіть, що вектори (-1; 2) і (0,5; -1) протилежно напрямлені

         7. Завдання з теми: «Рівні вектори»

Дано точки: А(3; -2), В(-4; 6), С(-2; -6), D(x; y). Знай­діть х і у, якщо = .

 

         8. «Як встановити рівність векторів»

Чи рівні і , якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)?

 

         9. Завдання з теми «Протилежні вектори»

 Доведіть, що вектори  і протилежні, якщо А(-1;2), В(2;-3), С(6;4), D(3; 9)

 

        3. Самостійне виконання вправ

Робота з картками:

1.Знайти координати векторів (3 бали)

І варіант  

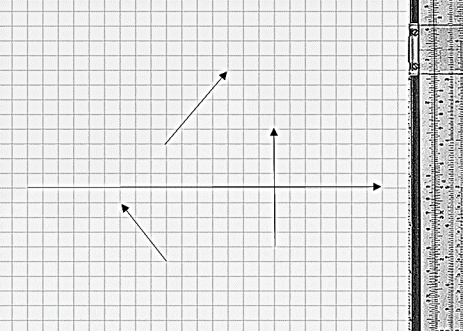
ІІ варіант

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

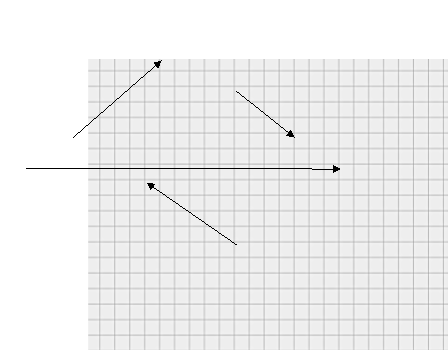
2. Завдання оцінюється 2 балами.

І варіант

При якому значенні m вектори (15; m) і (18; 12) колінеарні?

 

ІІ варіант

При якому значенні n вектори (2; n) і (6;12) колінеарні?

 

4. Робота в парах

1. Побудувати:     а+с;    2а-с;    в+2с-а

  а

 

 в 

                                      

                                                                                                            с

 

2. Побудувати:     а+с;    2а-с;    в-2с+а

  а

 

 в 

                                                  с

3. Побудувати:     а-с;    2а+с;    в-2с+а

  а

 

 в                       с

 

4. Побудувати:     с-а;    2а-с;    в+2с-а

  а

 

 в                             с

                         5.Побудувати:     а-с;    2а+с;    в-2с+а

  а

 

 в                          с

 

              Правильне виконання завдання оцінюється 3 балами ( Завдання фотографується та проектується на дошку для перевірки)

 

 

ІV. Підсумок уроку

Оголошення оцінок за урок

V. Домашнє завдання

 

1.  Побудуйте три вектори  та побудуйте вектор:

а) + – ; б) – + ; в) - + + ; г) – – .