Конспект уроку з геометрії для 9 класу на тему "Розв’язування трикутників"
В запропонованому конспекті уроку пропонуються різні прийоми і методи, які використовуються при вивчення теми «Розв'язування трикутників». При навчанні геометрії потрібно правильно підбирати задачі, які відображають прикладну спрямованість геометричних фактів, а також ілюструвати теоретичний матеріал різними прикладами із практики. Робота розрахована на широке коло творчо працюючих вчителів.
Урок геометрії в 9 класі
Тема. Розв’язування трикутників
Мета. Сформувати вміння знаходити кути і сторони трикутника, якщо відомі дві сторони і кут, протилежний одній із сторін або три сторони . Сприяти розвитку логічного мислення. Виховувати цілеспрямованість, інтерес до вивчення математики.
Тип уроку. Засвоєння нових знань і навичок.
Обладнання та наочність. Презентація, мультимедіа проектор.
Хід уроку
I.Організаційний етап.
II. Перевірка домашнього завдання.
Колективне розв’язування задач, аналогічних до тих, що були задані додому.
Задача 1. На будівництві залізниці потрібно на ділянці АВ прокласти тунель. За даними на малюнку поясніть, як знайти довжину тунелю.
Відповідь: 339 м.
Задача 2. Знайдіть відстань від точки А до недоступної точки, якщо АС = 50 м, ![]() САВ = 80°,
САВ = 80°, ![]() АСВ = 72°.
АСВ = 72°.
Відповідь: 101 м.
Індивідуальні завдання
![]() 1.Необхідно знайти відстань між заводом А і залізничною станцією В по іншу сторону річки, якщо АС = 100 м,
1.Необхідно знайти відстань між заводом А і залізничною станцією В по іншу сторону річки, якщо АС = 100 м, ![]() ВАС = 74°,
ВАС = 74°, ![]() ВСА = 44°.
ВСА = 44°.

![]()
![]()
![]()
![]()
Мал. 5
Відповідь: 79 м.
![]()
 2. Знайдіть відстань між недоступними точками А і В, якщо АС = 3 км, ВС = 5 км,
2. Знайдіть відстань між недоступними точками А і В, якщо АС = 3 км, ВС = 5 км, ![]() АСВ = 120°.
АСВ = 120°.

![]()
![]()
![]() Мал. 6
Мал. 6
Відповідь: 7 км.
III. Вивчення нового матеріалу.
Як ви вважаєте, чи можна виміряти висоту дерева, не підходячи до його основи? Чи можна виміряти відстань від одного берега річки до іншого, не перетинаючи річку? Такі задачі обов’язково будуть вами розв’язуватись у вашому майбутньому. Тому продовжимо розглядати випадки розв’язування трикутників.
Задача 3 (розв’язування трикутника за трьома сторонами)
Дано: а, b, с.
Знайти: ![]() А,
А, ![]() В,
В,![]() С.
С.
Розв’язання
-
За наслідком теореми косинусів соs
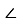 А =
А = 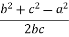 .
.
За допомогою калькулятора або таблиць знаходимо кут А.
-
Аналогічно соs
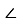 В =
В = 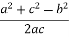 .
.
За допомогою калькулятора або таблиць знаходимо кут А.
-
За теоремою про суму кутів трикутника
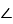 С = 180° - (
С = 180° - (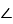 А +
А + 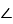 В).
В).
Самостійна робота з подальшою перевіркою.
Задача. Для фасадних робіт використовують конструкцію, схема якої показана на малюнку 7. Розрахувати кут АВС, якщо АВ = ВС = 7,5 м. Основа конструкції знаходиться на висоті 2 м. Висота будинку – 15 м.

Мал. 7
Відповідь: 120°.
Зауважимо, що для знаходження кутів у задачах 2 і 3 можна скористатися також теоремою синусів. Але при цьому слід пам’ятати, що будь-якому значенню синуса кута, меншому за одиницю, відповідатимуть два кути – гострий і тупий.
Задача 4 (розв’язування трикутника за двома сторонами й кутом, протилежним одній із них)
Дано: а, b ,![]() А.
А.
Знайти: с, ![]() В,
В,![]() С.
С.
Розв’язання
Якщо а > b, то кут В – гострий, бо лежить проти меншої сторони.
-
За теоремою синусів
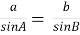 , звідки sin B =
, звідки sin B = 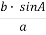 .
.
Знаходимо кут В, враховуючи, що проти більшої сторони трикутника лежить більший кут.
-
За теоремою про суму кутів трикутника
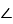 С = 180° - (
С = 180° - (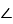 А +
А + 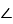 В).
В).
-
За теоремою синусів
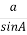 =
= 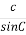 , звідки с =
, звідки с = 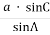 .
.
Якщо а < b. ( Кут А лежить проти меншої сторони, тому він обов’язково гострий і при ![]() А
А![]() 90° задача розв’язків не має).
90° задача розв’язків не має).
-
Знаходимо sin B =
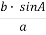 .
.
Якщо ![]() >1, задача розв’язків не має.
>1, задача розв’язків не має.
Якщо ![]() = 1, задача має єдиний розв’язок, оскільки трикутник прямокутний.
= 1, задача має єдиний розв’язок, оскільки трикутник прямокутний.
Якщо ![]() <1, задача має два розв’язки:
<1, задача має два розв’язки: ![]() В1 і
В1 і ![]() В2 (
В2 (![]() В2=180°-
В2=180°- ![]() В1).
В1).
-
Знаходимо
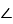 С1 і
С1 і 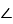 С2 .
С2 .
- Знаходимо с1 і с2.
Самостійна робота з подальшою перевіркою.
1.Дано: а = 17 см, b = 6 см ,![]() А = 156°.
А = 156°.
Знайти: с, ![]() В,
В,![]() С.
С.
Відповідь: ![]() В = 8°,
В = 8°,![]() С = 16° с = 11,5 см.
С = 16° с = 11,5 см.
2.Дано: b = 7 см, с = 8 см,![]() В = 65°
В = 65°
Знайти: а, ![]() А,
А,![]() С.
С.
Відповідь: задача не має розв’язку.
3.Дано: а = 6 см, b = 5 см ,![]() В = 50°.
В = 50°.
Знайти: с, ![]() А,
А,![]() С.
С.
Відповідь: с = 5,8 см, ![]() А = 67°,
А = 67°,![]() С = 63° або
С = 63° або
с = 1,9 см, ![]() А = 113°,
А = 113°,![]() С = 17°.
С = 17°.
IV. Підсумки уроку
Оцінювання роботи учнів.
Дати відповіді на запитання
1. Що я нового узнав на уроці?
2 . Над чим необхідно додатково попрацювати?
3. Які завдання для мене були найскладнішими?
V. Домашнє завдання (за підручником геометрії Єршової А.П.)
![]() 97(а), 100(а,б).
97(а), 100(а,б).


про публікацію авторської розробки
Додати розробку


