Презентація з геометрії 9 класу на тему : " Розв'язування прямокутних трикутників"
Про матеріал
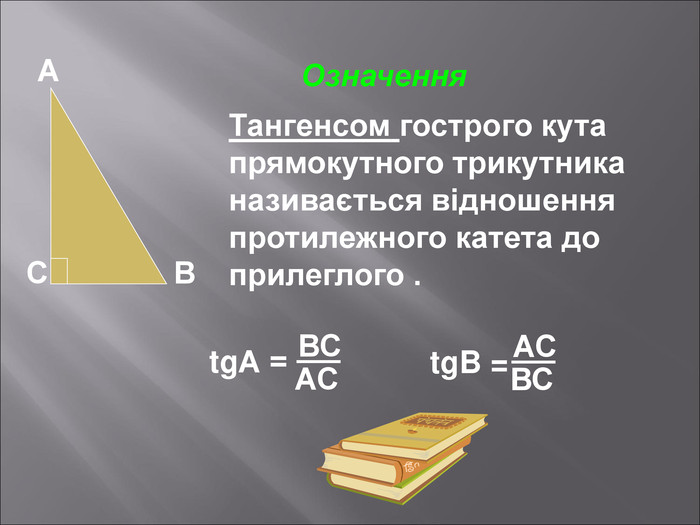
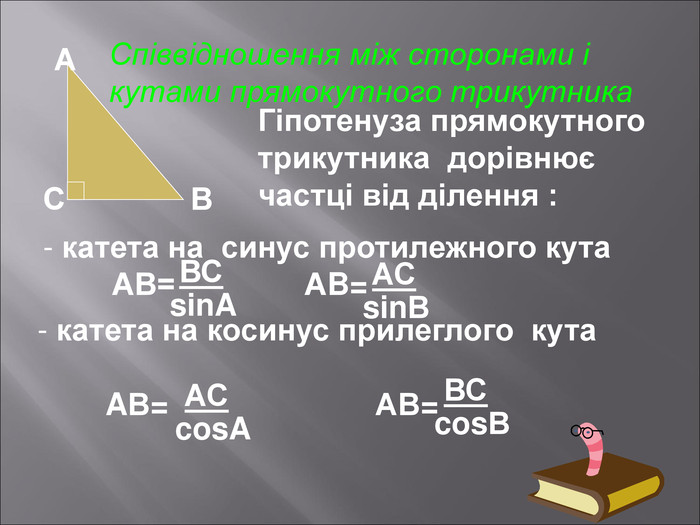
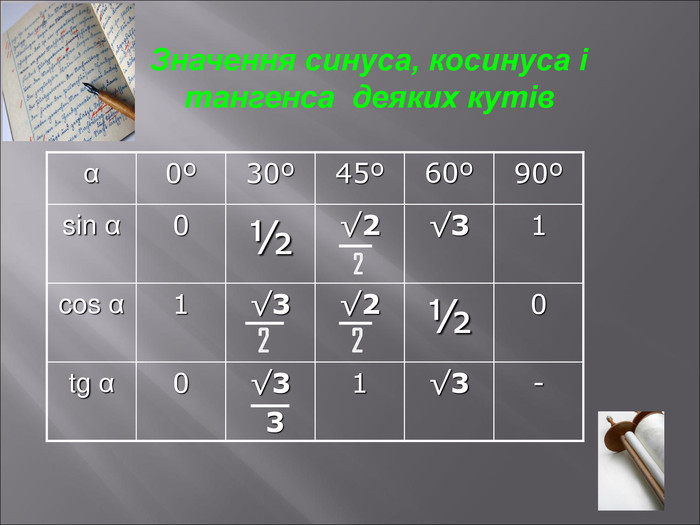
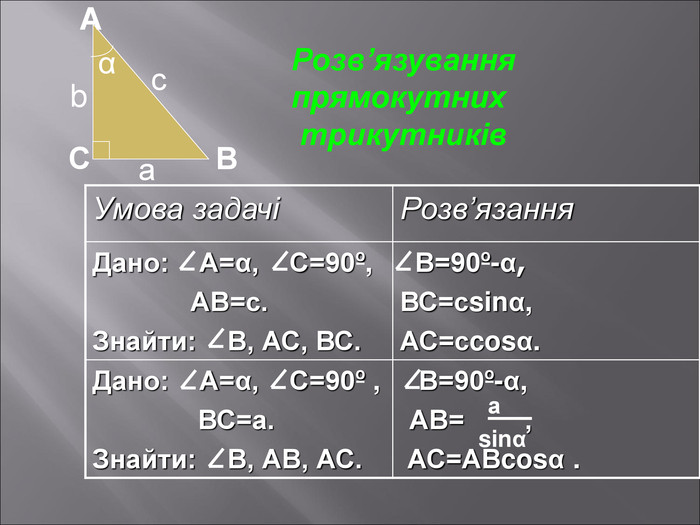
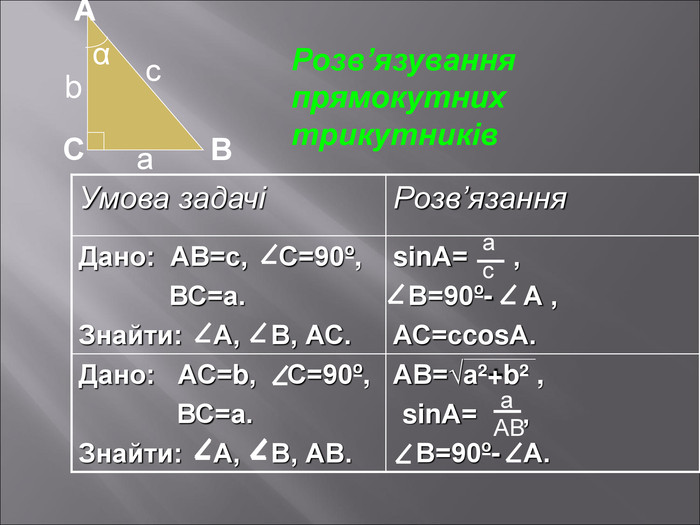
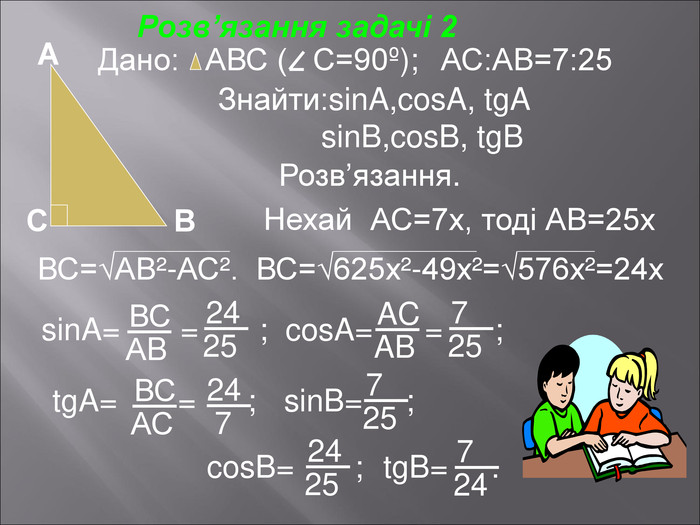
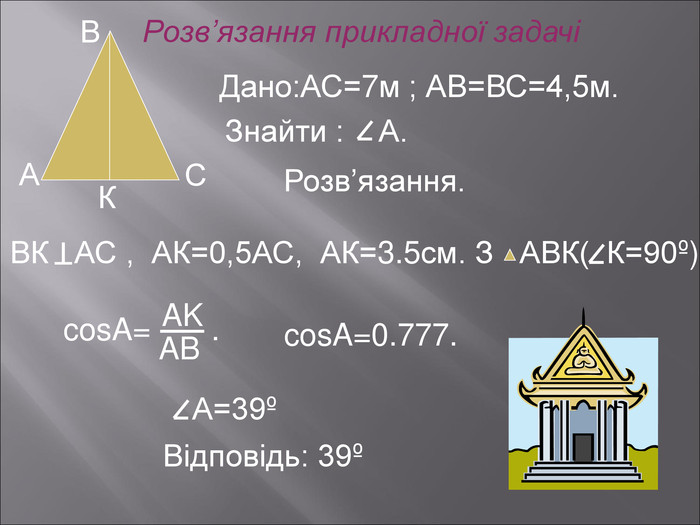
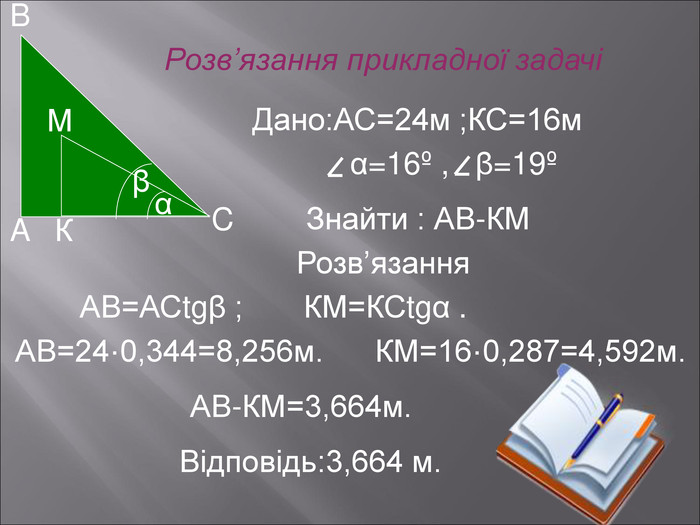
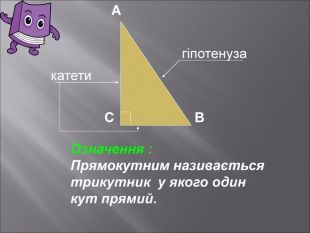
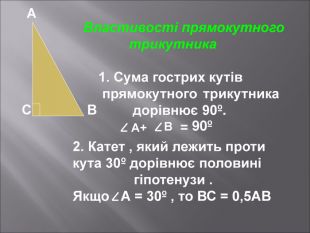
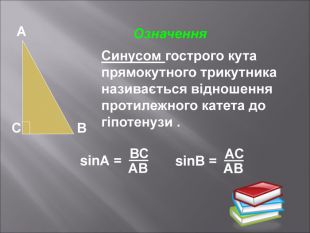
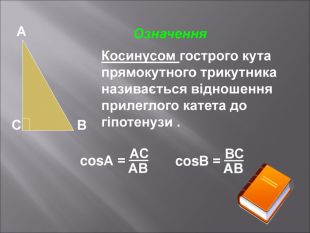
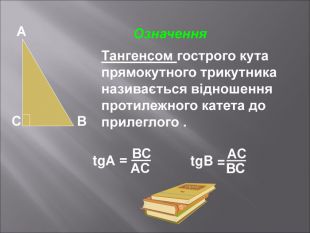
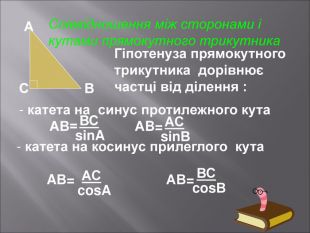
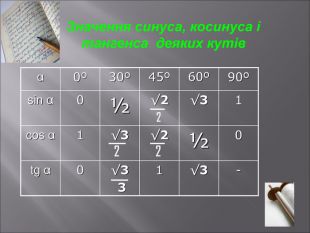
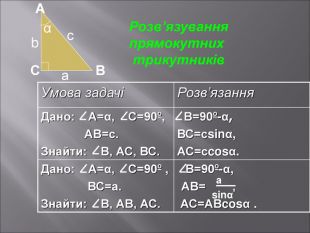
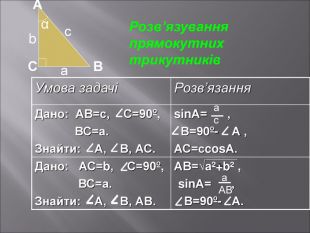
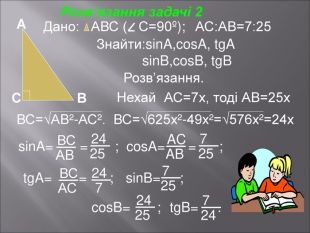
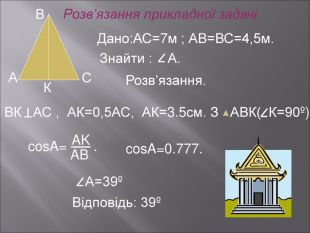
Даний матеріал буде корисним при вивченні теми" Розвязування прямокутних трикутників" ( геометрія 9 клас), Він містить весь потрібний теоретичний матеріал,а також схему розв'язання всіх чотирьох типів задач з даної теми; підібрані також задачі практичного змісту з повним їх розв'язанням.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку