Конспект уроку з геометрії для 9 класу на тему: «Розв’язування трикутників»

Конспект уроку з геометрії 9 клас.

Тема уроку: « Розв’язування трикутників».

Мета уроку:

узагальнити знання учнів з теми: ” Розв’язування трикутників”, застосування здобутих знань у різних умовах; формувати вміння учнів у застосуванні знань розв’язування трикутників до розв’язування прикладних задач.

розвивати вміння аналізувати, систематизувати та порівнювати, мислення, навиків самостійної роботи на різних етапах уроку; розвивати у учнів інтерес до математики шляхом розв’язування прикладних задач, формувати зацікавленість у результатах спільної роботи.

виховувати охайність, увагу, вміння говорити і слухати інших,  критичність і самокритичність.

Обладнання:

Картки з індивідуальними завданнями, картки для самостійної роботи,  картки-інформатори з теми: “ Розв’язування трикутників ”, мультимедійна дошка та проектор

 Тип уроку:

урок повторення, узагальнення і систематизації знань.

Метод:

репродуктивний, частково-пошуковий, пояснювально–ілюстративний.

Серед рівних розумом – за однакових інших умов –

переважає той, хто знає геометрію.

Б. Паскаль

«Математика безмежно різноманітна

як світ і присутня, міститься у всьому.»

М. П. Єругін

План уроку.

I. Організаційний момент. Повідомлення теми, мети, мотивація навчальної діяльності.  (Час: 3 хвилини.)

II. Узагальнення та систематизація теоретичних відомостей з теми. (Час: 7 хвилин.)

III. Перевірка домашньої роботи груп. (Час: 10 хвилин.)

IV. Формування вмінь учнів застосовувати знання з розв’язування трикутників до розв’язування прикладних задач. (Час: 10 хвилин.)

V. Самостійна робота. (Час: 8 хвилин.)

VI. Підбиття підсумків уроку. (Час: 4 хвилин.)

VII. Домашнє завдання. (Час: 3 хвилин.)

Хід уроку.

І. Організаційний момент

Повідомлення теми та мети уроку. Епіграф.

Мотивація навчальної діяльності: Слова вчителя.

Розв’язати трикутник – це означає за кількома відомими його елементами знайти всі інші його елементи. Ще понад два тисячоліття тому було створено окрему науку про розв’язування трикутників – тригонометрію. Трикутники в геометрії відіграють важливу роль. В багатьох відношеннях вони найпростіші з усіх многокутників, тому ними порівняно легко користуватися. Навіть кожний многокутник можна розрізати на кілька трикутників.

Використовують «розв’язування трикутників» для розв’язування прикладних задач. Прикладними задачами в математиці називають задачі, умови яких містять нематематичні поняття. Розв’язуючи такі задачі математичними методами, звичайно створюють їх математичні моделі. В геометрії математичні моделі найчастіше створюють з геометричних фігур, чисел, виразів, рівнянь, функцій тощо. Щоб створити потрібну математичну модель прикладної задачі, треба знати не тільки математику, а й ту галузь науки чи виробництва, якої стосується дана задача. З «розв’язуванням трикутників» найчастіше пов’язані різні просторові об’єкти, споруди, механізми тощо.

Сьогодні на уроці ми розглянемо прикладні задачі, які можна моделювати за допомогою трикутників.

ІІ. Узагальнення та систематизація теоретичних відомостей з теми

(відбувається у вигляді фронтальної бесіди)

Сформулюйте теорему косинусів

Поясніть як із формули знайти

Як можна визначити вид трикутника за кутами, якщо відомі сторони а, в, с.

Сформулюйте теорему косинусів

Сформулюйте наслідок про співвідношення між кутами трикутника і протилежними кутами

Як можна знайти радіус кола описаного навколо трикутника, у якому відомі сторони і протилежні кути?

Які є основні випадки розв’язування довільних трикутників?

Кожному питанню актуалізації присвячено окремий слайд: спочатку на екрані з’являється запитання до класу, а після обговорення – відповідь.

ІІІ. Перевірка домашньої роботи груп

На попередньому уроці вчитель розбив клас на три групи. Кожна група отримала задачу практичного характеру:

Перша група:

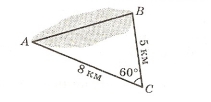
На будівництві залізниці потрібно на ділянці АВ прокласти тунель (мал. 1). За даними на малюнку поясніть, як знайти довжину і напрям тунелю. Обчисліть довжину тунелю.

Мал. 1

Друга група:

Знайдіть відстань від точки А до недоступної точки , якщо АС=50м, кут САВ= , кут АСВ= (мал. 2)

Мал. 2

Третя група:

Футбольний м’яч знаходиться в точці А футбольного поля на відстані 4,5 метрів і 9,4 метрів від основ В і С стійок воріт (мал. 3). Футболіст направляє м’яч у ворота. Знайдіть кут  влучення м’яча у ворота, якщо ширина воріт 7 метрів.

Мал. 3

В задачах учні показують як можна використати на практиці знання теореми косинусів і синусів та їх наслідки.

Кожній умові задачі присвячено слайд. Розв’язування задачі учні показують на дошці. Інші учні цієї групи доповнюють відповідь, та говорять який випадок розв’язування трикутників вони використали.

Підвищення мотивації навчальної діяльності: Ще у Київській Могилянській академії Феофан Прокопович ознайомлював учнів з вимірювальними роботами на місцевості. Починав він цей курс так: « Спеціальна геометрія, яку іноді називають практичною геометрією, а іноді геодезією, є однією з найшляхетніших, найкорисніших і найцікавіших галузей математики. Адже вона займається не лише вимірюванням землі, від чого колись і дістала свою назву, а вимірює все, що підлягає вимірюванню…»

IV. Формування вмінь учнів застосовувати знання з розв’язування трикутників до розв’язування прикладних задач

Розв’язування прикладних задач ґрунтується на розв’язуванні трикутників.

Сьогодні на уроці ми розглянемо таки види задач (слайди):

Задачі на знаходження відстані до недоступного пункту

Задачі на знаходження відстані між двома доступними пунктами, якщо безпосереднє вимірювання неможливе.

Задачі на знаходження висот предмета, основа якого недоступна.

Задачі першого та другого типу учні розібрали вдома, тому по готовим малюнкам цих задач складають план. Один з учнів відповідної групи пише план на дошці.

Задача типу 1

Знайти відстань від пункту А до недоступного пункту В. (мал. 4)

Мал. 4

Задача типу 2

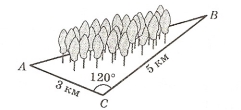
Знайдіть відстань між пунктами В і С, розділеними ставком (мал. 5).

Мал. 5

Тепер розглянемо задачу на знаходження висот предмета, основа якого недоступна.

Задача типу 3

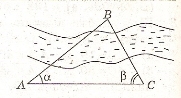
Знайти висоту вежі, яка відокремлена від вас річкою (мал. 6)

Мал. 6

Розв’язання

На горизонтальній прямій, яка проходить через основу вежі, позначимо дві точки  та .

Виміряємо

За теоремою синусів, з трикутника АВС дістанемо:
 

Розглянемо трикутник ABD: BD=АВ*,

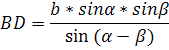
Запишемо ВК:

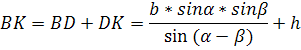
Весь клас розв’язує задачу, якщо вимірювання такі:

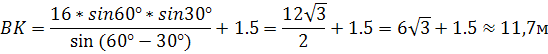
Задача

Дві сили та утворюють кут . Знайти їх рівнодійну, якщо:

Відповідь: 6.7н

V. Самостійна робота

VI. Підбиття підсумків уроку

Запитання до класу

Що означає розв’язати трикутник?

Складіть план розв’язування трикутників, якщо задано:

а) сторону b і два кути ;   б) дві сторони a і b та кут між ними .

Мотивація навчальної діяльності: Дуже багато життєвих та прикладних  задач та завдань ДПА присвячені темі « Розв’язування трикутників». Тому на цю тему необхідно звернути вашу особливу увагу, якщо ви бажаєте добре скласти іспити і отримати гарну освіту.

VII. Домашнє завдання ( вчитель дає з поясненням)

Розділ 1, § 1-5.

1. № 145(1), № 146(2) стор.  35  

2. № 169 стор. 37 ( застосування на практиці)

3*.№171 стор.38 ( застосування на практиці)