Конспект уроку з геометрії "Площа многокутників" з інноваційними технологіями. 8 клас

Конспект уроку «Площа многокутників.

Мета:

• створити умови для закріплення знань, умінь і навичок учнів по темі «Площі многокутників»;
• узагальнити  та систематизувати теоретичні  знання  учнів з даної теми, ознайомити учнів із завданнями по даній темі із ЗНО;
• розвивати навички самоконтролю та взаємоконтролю, вміння лаконічно математично грамотно висловлювати свою думку, критичність, логічність мислення, інтерес до предмета, інтерес до процесу навчання, застосовувати набуті знання до розв’язування вправ у стандартних та нестандартних ситуаціях;
• виховувати самостійність, уміння самоорганізовуватись; відповідальність, стійкість, наполегливість, взаємо повагу один до одного.

Тип уроку: узагальнення та систематизації знань.

Обладнання:картки з задачами;  таблиці з формулами.

І) Виконання усних вправ:

1.        На підлозі розстелені два килими: один площею 6 м², другий — 8 м². Килими частково накладені один на одного — по фігурі, площа якої дорівнює 1 м². Яку площу підлоги закривають килими?
2.        Під час вимірювання площ земельних ділянок використовують різ­ні одиниці вимірювання. Що означає гектар; ар?
3.        Що означає «сотка» городу?
4.        Чи одне й те саме означають ар і сотка?
5.        Чи правильні твердження?

а) Кожний квадрат є прямокутником.

в) Жодний прямокутник не є ромбом.

г) Існує квадрат, який не є ромбом.

6.Периметр квадрата дорівнює 32. Чому дорівнює площа цього квад­рата?

7.При однаковім периметрі який  чотирикутник  буде мати найбільшу площу?

Згадаємо формули для обчислення площ многокутників.

ІІ) Встановити відповідність:

Відповіді: 1Г, 2Б, 3Д, 4А, 5Є, 6Ж, 7В, 8Е

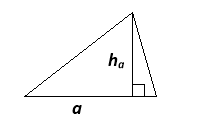
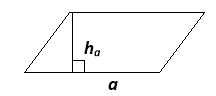
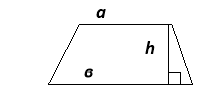
6.          Площу якої фігури  можна  обчислити за такими формулами:

S=

S=a

S = a²

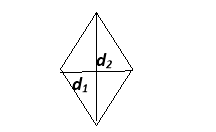
S=d²

ІІІ) Розв’язування задач по темі "Площі многокутників"

Усні вправи (Рисунки зображені на дошці)

Задача 1

           А                 7            В      АВСД- квадрат

                                                          S-?    

          С                                       Д

Задача 2

                                                          S-?

              5                            5

                             8

Задача 3

                                                                                S-?

     10

        6                  8                                             

Задача 4

                                                            S=25 см²

                                                        Знайти Р-?

ІV) Тестові завдання (можна набрати 10 балів)

1.Катети прямокутного трикутника 10 і 15 см. Обчислити площу трикутника.

1бал

2.Знайти площу паралелограма, сторона якого 12, а висота, проведена до неї, 8.

1бал

3.Знайти площу прямокутного трикутника, якщо його висота ділить гіпотенузу на відрізки 8 см і 18 см.

 2бали

4.Бісектриса кута прямокутника ділить його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки варіантів розв’язування має задача?

2бали

5.Знайти площу рівнобічної трапеції основи якої 14 см і 30 см, а бічна сторона дорівнює 17см.

2бали

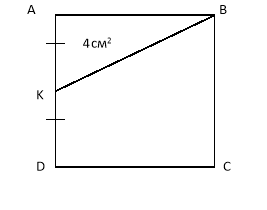
6. Пряма ВК проходить через середину сторони квадрата АВСД. Знайти площу квадрата АВСД, якщо S_ABC = 4см² .

2бали