Конспект уроку з геометрії "Правильна піраміда"

Тема: Правильна піраміда

Мета: навчальна – сформувати поняття правильної піраміди, апофеми правильної піраміди; домогтися засвоєння властивостей правильної піраміди. Сформувати вміння розв'язувати задачі на знаходження елементів правильної піраміди.

розвивальна – розвивати графічну культуру учнів, просторову уяву, розширювати знання математичної термінології.

виховна – виховувати культуру математичної мови, зібраність, охайність, інтерес до математики.

Тип уроку: урок засвоєння нових знань, формування вмінь і навичок.

Обладнання: презентація «Правильна піраміда», моделі правильних пірамід.

Очікувані результати:

після уроку учні зможуть:

• вирізняти правильні піраміди серед інших пірамід;
• будувати правильні піраміди та знаходити їх елементи;
• розв'язувати задачі з використанням властивостей правильної піраміди.

Хід уроку

1). Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

2). Перевірка домашнього завдання.

Проводиться обговорення розв'язку задачі № 798 (Підручник «Геометрія 11 клас » Г.П. Бевз, В. Г. Бевз, Н. Г. Владімірова, В.М. Владіміров ).

Учні коментують розв'язання з використанням готового малюнка.

• Яка точка є основою висоти піраміди, якщо всі бічні ребра піраміди рівні?
• Яке коло називається описаним навколо многокутника?

 

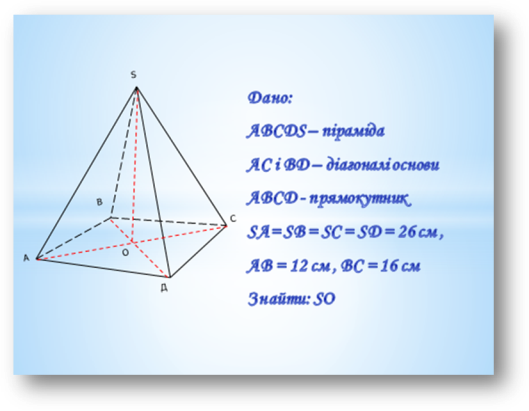
Розв’язання:

Точка О – центр описаного кола (точка перетину діагоналей)

∆ ASO – прямокутний. За теоремою Піфагора: = +

SО = .

∆ AВС – прямокутний. За теоремою Піфагора: = +

АС = = 20 (см).

АО = АС = 10 (см)

SО = = 24 (см)

Відповідь: 24 см .

З метою перевірки засвоєння учнями теоретичного матеріалу з учнями проводиться графічний диктант.

Правильна відповідь

Неправильна відповідь

Чи правильно, що:

• якщо бічні ребра піраміди утворюють рівні кути з висотою піраміди, то основою висоти є центр кола, вписаного в піраміду;
• якщо висоти всіх бічних граней, проведені з вершини піраміди, рівні, то основою висоти є центр кола, вписаного в основу піраміди;
• якщо бічні ребра піраміди рівні і її основою є тупокутний трикутник, то основа висоти лежить поза основою піраміди;
• якщо бічні ребра піраміди рівні і її основою є прямокутний трикутник, то основа висоти лежить усередині трикутника;
• якщо бічні ребра піраміди рівні і її основою є прямокутний трикутник, то основою висоти є середина гіпотенузи трикутника;
• у піраміди може бути дві бічні грані, які перпендикулярні до основи;
• у піраміди може бути три бічні грані, які перпендикулярні до основи;
• якщо одна з бічних граней піраміди перпендикулярна до площини основи, то висота піраміди збігається з висотою цієї грані;
• якщо всі бічні ребра піраміди рівні, то основою висоти піраміди є центр кола, описаного навколо основи піраміди.

Учні обмінюються зошитами та проводять взаємоперевірку. Після цього обговорюємо питання, при відповіді на які, були допущені помилки.

3). Мотивація навчальної діяльності, формування мети й завдань уроку.

Створюємо відповідну мотивацію за допомогою проблемної ситуації. Пропоную учням пригадати означення правильної призми і за аналогією сформулювати означення правильної піраміди.

Учитель повідомляє, що крім того, що основою правильної піраміди є правильний многокутник, піраміда має задовольняти ще одну умову і тільки в  тому випадку вона буде називатися правильною.

Отже, завданням уроку є засвоєння означення та властивостей правильної піраміди, навчитись будувати правильну піраміду, розв'язувати задачі на знаходження елементів правильної піраміди.

4). Актуалізація знань учнів

А). Актуалізація знань з планіметрії.

• Сформулюйте ознаки рівності прямокутних трикутників.
• Доведіть рівність прямокутних трикутників.
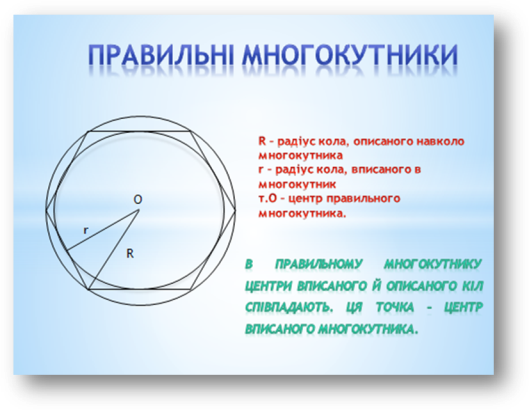
• Дати означення правильного многокутника. Як визначити центр правильного многокутника?

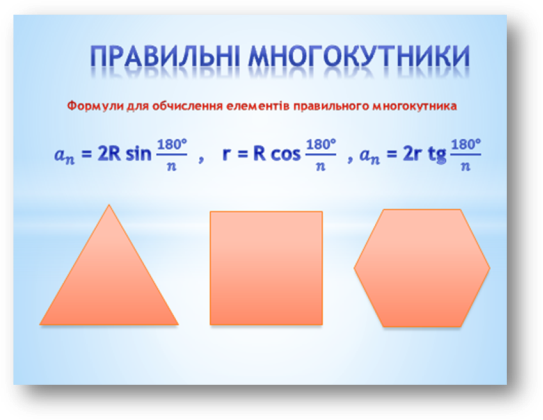
• Повторення формул для обчислення елементів правильного многокутника.

Б). Актуалізація знань із стереометрії.

• Сформулюйте теорему про три перпендикуляри.
• Сформулюйте означення кута між прямою і площиною та кута між площинами.
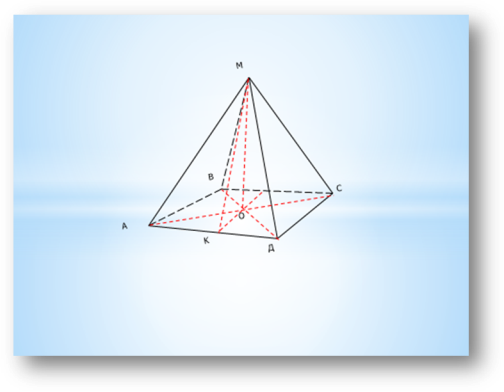
• Скориставшись рисунком, укажіть:

1. кут між бічним ребром АС та площиною основи піраміди;
2. кут між бічною гранню АМД і основою піраміди.

                 

5). Вивчення нового матеріалу.

Означення правильної піраміди. Зображення правильної піраміди.

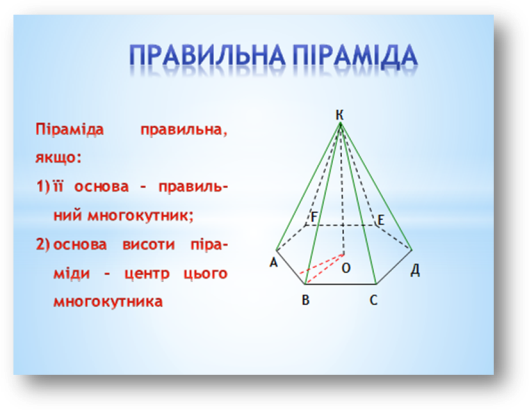
Одним із прикладів правильної піраміди є єгипетські піраміди. Це чотирикутні піраміди.

Увага учнів звертається також на зображення правильної трикутної і шестикутної пірамід.

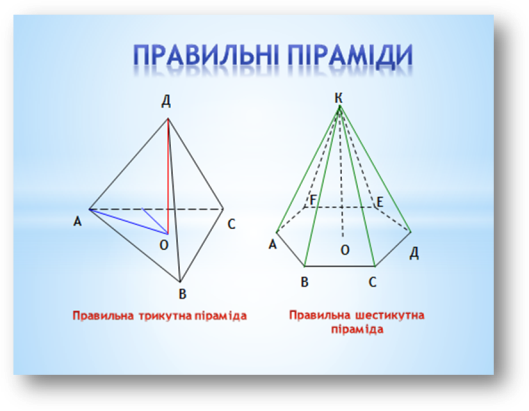
Графічне завдання для учнів: виконати в зошиті зображення правильної шестикутної піраміди.

Властивості правильної піраміди.

Всі бічні ребра правильної піраміди рівні, а бічні грані – рівнобедрені трикутники.

 

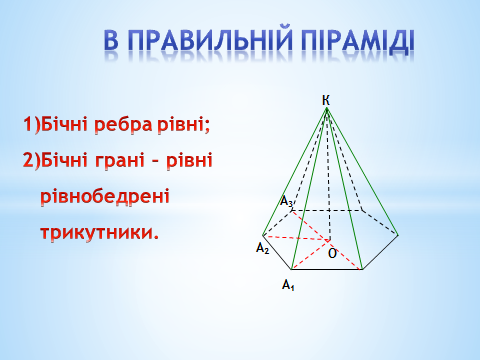
Доведення даних фактів проводиться усно:

 

1. Будь – яке бічне ребро є гіпотенузою прямокутного трикутника, одним з катетів якого є висота піраміди, а другим – радіус кола, описаного навколо основи. Ці прямокутні трикутники рівні (за двома катетами). Отже, їх гіпотенузи також рівні.

 

2. Так як бічні ребра правильної піраміди рівні, то її бічні грані – рівнобедрені трикутники. Так як А₁А₂ … А_n  - правильний многокутник, то основи цих трикутників також рівні між собою. Отже, бічні грані рівні (за трьома сторонами)

Апофема

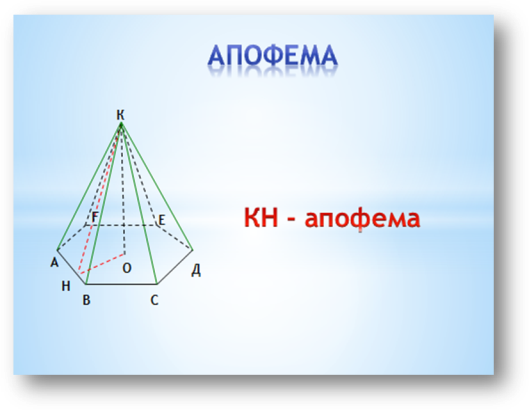
Апофема – висота бічної грані правильної піраміди, проведена з її вершини. Цей термін вживається тільки для правильної піраміди, хоча у неправильної піраміди також можуть бути рівні висоти бічних граней.

Питання до учнів:

• Скільки апофем у правильній піраміді?
• Чи рівні апофеми правильної піраміди? Чому?
• Скільки висот у піраміди?

Графічне завдання: провести апофему правильної шестикутної піраміди.

6). Закріплення вивченого матеріалу.

Розв'язування задачі на побудову

В правильній шестикутній піраміді побудувати:

• кут між бічним ребром і площиною основи;

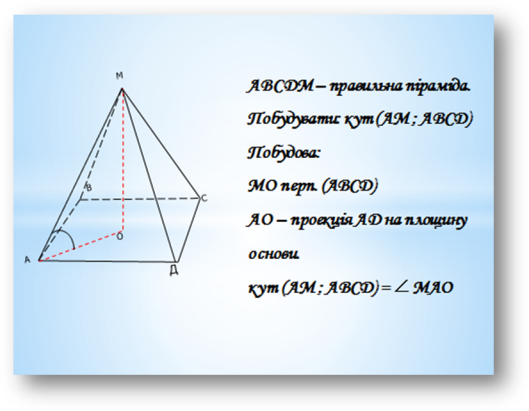
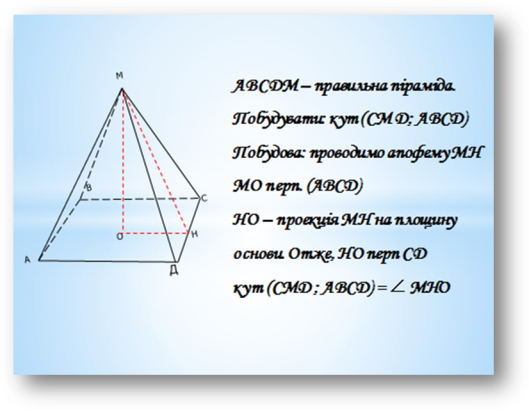
• лінійний кут двогранного кута при основі.

Розв'язати задачу:

Площа бічної грані правильної чотирикутної піраміди дорівнює 48 см² , а периметр основи – 12 см. Обчисліть апофему піраміди.

• Який чотирикутник лежить в основі правильної піраміди?
• Що є бічними гранями правильної піраміди?
• Де лежить основа висоти піраміди?
• Як побудувати апофему піраміди?

Розв'язання задачі:

Р_АВСД = 12 см, отже, АВ = ВС = СД = АД = 12 : 4 = 3 (см)

– рівнобедрений (за властивістю правильної піраміди)

SM – висота

= ДС ∙ SM;

SM =  ;

SM = 32 (см).

7). Підведення підсумків уроку.

• Яка піраміда називається правильною?
• Запишіть співвідношення між бічним ребром b, апофемою l, радіусами r і R вписаного та описаного кіл основи правильної піраміди.
• Чи можна піраміду назвати правильною, якщо:

1. її основою є квадрат, а основою висоти – вершина квадрата;
2. її основою є прямокутник, а основою висоти – точка перетину діагоналей прямокутника;
3. її основою є рівносторонній трикутник, а основою висоти – точка перетину медіан трикутника.

8). Домашнє завдання

Вивчити зміст понять, розглянутих на уроці §22.

Виконати № 796

Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147 м, а площа основи – 5,3 га. Знайдіть міру двогранного кута при ребрі її основи і кут нахилу до площини основи її бічного ребра.

Виконати № 797

Площа діагонального перерізу правильної чотирикутної піраміди вдвічі менша за площу основи. Доведіть, що протилежні бічні ребра піраміди перпендикулярні.

Урок закінчено. Можете бути вільні.