Конспект уроку з математики для 5 класу на тему: Самостійна робота з теми "Звичайні дроби"
Математика
Тема уроку: Самостійна робота
Мета уроку: перевірити знання учнів під час виконання самостійної роботи.
Тип уроку: перевірка знань, умінь, навичок.
Обладнання та наочність: самостійний аркуш, лінійка, олівець, ручка .
Дата проведення: 5-Б – 26.01.2015
Хід уроку
І. ОРГАНІЗАЦІЙНИЙ ЕТАП
- Привітання вчителя і учнів.
- Організація готовності учнів до уроку, налаштування їх на роботу.
ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Математичний диктант.
- Два дроби з однаковими знаменниками рівні, якщо їх чисельники рівні.
- Із двох дробів з однаковими знаменниками більший (менший) той дріб, у якого чисельник більший ( чисельник менший).
-
Дріб – це вираз виду
 , де a – називається чисельником, а b – знаменником дробу, риска дробу « –» – означає дію ділення.
, де a – називається чисельником, а b – знаменником дробу, риска дробу « –» – означає дію ділення.
- Що показує знаменник дробу? Чисельник дробу?
(Відповідь: знаменник показує на скільки частин поділена одиниця(ціле), а чисельник – скільки цілих частин взято.)
- Правильний дріб завжди менший від 1.
- Неправильний – більший за 1 або дорівнює 1.
- Які дроби називають правильними? (у яких a b).Які неправильними?
( у яких аb або a=b).
- Що означає риска дробу? ( дію ділення).
ІІІ. ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ
- Сьогодні на уроці ми з вами проведемо «Самостійну роботу».
- Мета сьогоднішнього уроку: перевірка ваших знань, отриманих протягом попередніх уроків.
IV. САМОСТІЙНА РОБОТА
Варіант 1.
Початковий рівень ( 1 завдання – 0,5 балів)
-
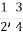 – приклади звичайних…
– приклади звичайних…
-
У запису
 число a – це … дробу, він показує…
число a – це … дробу, він показує…
-
Дріб
 , у якого m<n, називається … дробом.
, у якого m<n, називається … дробом.
- З двох дробів із однаковими знаменниками більший той, у якого…
- Усі неправильні дроби … або дорівнюють …
- Результат ділення m : n можна записати у вигляді дробу…
-
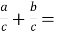 …
…
- Риску дробу можна розглядати як знак…
-
Неправильний дріб
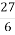 можна записати у вигляді … числа.
можна записати у вигляді … числа.
-
Щоб знайти
 від числа 15, треба _:__.
від числа 15, треба _:__.
Середній рівень ( 1-4 завдання – 0, 5 балів, 5-8 – 1 бал )
-



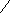

 Визначте, яка частина фігури, зображеної на рисунку, заштрихована.
Визначте, яка частина фігури, зображеної на рисунку, заштрихована.

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]() а) б) в) г)
а) б) в) г)
![]()
-
Знайдіть
 від 36.
від 36.
А 54 Б 24 В 12 Г 72
-
Знайдіть число, якщо
 його становлять 12.
його становлять 12.
А 16 Б 9 В 48 Г 36
- Порівняйте:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Обчисліть значення виразу:
![]() …
…
- Перетворіть неправильний дріб у мішане число:
а) ![]() …; б)
…; б) ![]() …
…
- Перетворіть мішане число у неправильний дріб:
а) ![]() …; б)
…; б) ![]() …
…
- Знайдіть значення виразу:
![]() …
…
Достатній і високий рівні ( 1 завдання – 3 бали )
- Запишіть у вигляді дробів 1, 3, 5, 15, 20 частин числа, яке поділили на 40 рівних частин.
-
Накресліть координатний промінь. Виберіть зручний одиничний відрізок і позначте на промені такі точки A
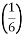 , B
, B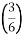 , C
, C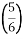 , D
, D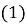 , E
, E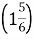 .
.
-
Додайте
 числа 244 до
числа 244 до 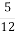 числа 600.
числа 600.
-
У 5 – А класі навчаються 32 учні,
 із них займаються у шкільному математичному гуртку. Знайдіть загальну кількість членів цього гуртка, якщо кількість учнів 5 – А класу становить від неї
із них займаються у шкільному математичному гуртку. Знайдіть загальну кількість членів цього гуртка, якщо кількість учнів 5 – А класу становить від неї  .
.
Варіант 2.
Початковий рівень ( 1 завдання – 0,5 балів)
-
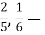 приклади … дробів.
приклади … дробів.
-
У запису
 число b – це … дробу, він показує…
число b – це … дробу, він показує…
-
Дріб
 , у якого m n, називається … дробом.
, у якого m n, називається … дробом.
-
Якщо
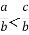 , то a … c.
, то a … c.
- Усі правильні дроби … від одиниці.
-
Дріб
 можна розглядати як результат дії …
можна розглядати як результат дії …
-
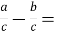 …
…
-
Запис
 можна читати так: « … ».
можна читати так: « … ».
-
Мішане число
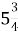 можна записати у вигляді дробу: …
можна записати у вигляді дробу: …
-
Щоб знайти число, від якого взяли
 і отримали 15, треба _:__.
і отримали 15, треба _:__.
Середній рівень ( 1-4 завдання – 0, 5 балів, 5-8 – 1 бал )
-



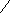








 Визначте, яка частина фігури, зображеної на рисунку, заштрихована.
Визначте, яка частина фігури, зображеної на рисунку, заштрихована.

![]()
![]()

![]()
![]()


![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а) б) в) г)
а) б) в) г)
-
Знайдіть
 від 48.
від 48.
А 72 Б 32 В 16 Г 96
-
Знайдіть число, якщо
 його становлять 24.
його становлять 24.
А 32 Б 18 В 48 Г 72
- Порівняйте:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Обчисліть значення виразу:
![]() …
…
- Перетворіть неправильний дріб у мішане число:
а) ![]() …; б)
…; б) ![]() …
…
- Перетворіть мішане число у неправильний дріб:
а) ![]() …; б)
…; б) ![]() …
…
- Знайдіть значення виразу:
![]() …
…
Достатній і високий рівні ( 1 завдання – 3 бали )
- Запишіть у вигляді дробів 1, 3, 5, 15, 20 частин числа, яке поділили на 60 рівних частин.
-
Накресліть координатний промінь. Виберіть зручний одиничний відрізок і позначте на промені такі точки M
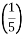 , N
, N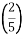 , P
, P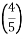 , R
, R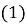 , S
, S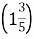 .
.
-
Додайте
 числа 244 до
числа 244 до 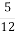 числа 300.
числа 300.
-
У 5 – А класі навчаються 32 учні,
 із них займаються у шкільному математичному гуртку. Знайдіть загальну кількість членів цього гуртка, якщо кількість учнів 5 – А класу становить від неї
із них займаються у шкільному математичному гуртку. Знайдіть загальну кількість членів цього гуртка, якщо кількість учнів 5 – А класу становить від неї  .
.
V. ПІДСУМКИ УРОКУ
- Підсумкова бесіда
- Які завдання давалися найважче? Чому?
2. Відповісти на питання, що виникли у дітей під час виконання Самостійної роботи.
VІ. ДОМАШНЄ ЗАВДАННЯ
- Завдання за підручником: Н.А. Тарасенкова, І.М. Богатирьова, О.П. Бочко, О.М. Коломієць, З.О. Сердюк. Розділ V, § 24, № 923, 934, 944, 948.
- Інструктаж:
- № 923 подібний до № 922.
- № 934 подібний до № 933. Щоб виконати цю вправу вам необхідно повторити правило виділення цілої частини з неправильного дробу, знаючи це правило дану вправу ви виконаєте без проблем.
- № 944. Подібний до № 943. Щоб виконати цю вправу вам також знадобиться правило виділення цілої частини з неправильного дробу.
- № 948 подібний до № 947. Щоб виконати цю вправу без проблем, вам необхідно повторити правило перетворення мішаного числа у неправильний дріб.
- І обов’язково почитайте § 24, і вивчіть всі основні правила.
1


про публікацію авторської розробки
Додати розробку
