Конспект уроку за темою "Квадрат двочлена"
Урок №43.
Мета: домогтися свідомого розуміння учнями змісту формул «квадрат суми» та «квадрат різниці двох виразів»; виробити первинні вміння застосовувати ці формули для перетворення квадрата двочлена у многочлен стандартного вигляду.
Тип уроку: засвоєння знань.
Хід уроку
І. Аналіз тематичної контрольної роботи
Вчитель приділяє на цьому уроці 5–10 хвилин навчального часу на пояснення розв’язання найскладніших задач.
ІІ. Актуалізація опорних знань
1. Подайте у вигляді добутку: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2. Знайдіть добуток: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
3. Прочитайте словами вирази (використовуючи поняття «сума», «різниця», «квадрат», «добуток» і т. д.):
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() та
та ![]() ;
; ![]() та
та ![]() ;
; ![]() та
та ![]() .
.
4. Порівняйте: ![]() та
та ![]() ;
; ![]() та
та ![]() ;
; ![]() та
та ![]() .
.
IV. Засвоєння знань
Запис формул та прикладів у зошити може мати такий вигляд:
|
Конспект 12 Квадрат суми двох виразів |
|||
|
Квадрат суми двох виразів |
= квадрат першого виразу |
+ подвоєний добуток першого та другого |
+ квадрат другого виразу |
|
Формула
|
|
|
|
|
Приклади |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Квадрат різниці двох виразів |
|||
|
Квадрат різниці двох виразів |
= квадрат першого виразу |
– подвоєний добуток першого та другого |
+ квадрат другого виразу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V. Засвоєння вмінь
Виконання усних вправ
1. Прочитайте рівності. Чи є вони тотожностями? Чому?
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
2. Піднесіть до квадрата двочлен:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
2. Подайте вираз у вигляді суми:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) 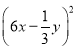 ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) 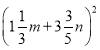 ;
;
11) ![]() ; 12)
; 12) ![]() .
.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
VI. Підсумки уроку
Допишіть замість (*) такі вирази, щоб рівності стали правильними:
![]() ;
; ![]() .
.
VII. Домашнє завдання
№ 1. Використовуючи формули «квадрат двочлена», перетворіть у суму вирази:
6) 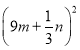 ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ;
;
11) ![]() ; 12)
; 12) ![]() .
.
№ 2. 1) Піднесіть до квадрата вирази: ![]() ;
; ![]() ;
; ![]() .
.
2) Замініть вирази на протилежні. Як це зробити? Запишіть утворені вирази у вигляді суми та піднесіть до квадрата за формулою «квадрат суми двох виразів».
Спростіть утворені многочлени та порівняйте їх із многочленами, здобутими в попередньому пункті.


про публікацію авторської розробки
Додати розробку
