Конспект відкритого уроку на тему "Трикутник"

Тема уроку. Трикутники

Мета уроку.  Узагальнити та систематизувати навчальний матеріал по темі «Трикутники».

                        Вдосконалювати уміння та навички учнів розв’язувати задачі, виконувати тестові

                        завдання.

                        Розвивати уяву, логічне та образне мислення

                        Виховувати інтерес до вивчення математики, гордість за людей, які прославили

                        наш край.

Тип уроку. Урок узагальнюючого повторення

Обладнання. Комп’ютер, інтерактивна дошка, проектор, програмне забезпечення: мультимедійна презентація «Трикутники» у програмі Microsoft Power Point,  тестові завдання у програмі My Test

План та хід уроку

І. Організаційна частина

Символічна назва нашого сьогоднішнього уроку «Сходинками до вершин». Піднімаючись сходинками, ми і  повторимо  навчальний матеріал по темі «Трикутники».

Трикутник – одна з перших геометричних фігур, про властивості якої людство дізналося ще в давнину. Задачі про трикутник були знайдені у давньогрецьких папірусах, старовинних індійських книгах. У папірусі Ахмеса згадується про рівнобедрений  і прямокутний трикутники. А давні вавилоняни 4000 років тому вже знали про властивість кутів при основі рівнобедреного трикутника.

Трикутник – це одна з перших геометричних фігур, про властивості якої ми вивчили в курсі геометрії 7-го класу.

То ж  сьогодні ми і піднімемося такими сходинками:

- пасивне повторення,

- активне повторення,

- бліц-опитування,

- усні вправи,

- задачі за готовим малюнком,

- тестові завдання,

- образно-логічний диктант,

- сторінка цікавої математики,

- серенада математиці.

ІІ. Повторення й узагальнення понять і засвоєння відповідної їм системи знань

1. Перша сходинка - пасивне повторення

 Протягом трьох хвилин звучить музика і учні знайомляться з презентацією «Трикутники». На дошку проектуються слайди з коротким викладом теоретичного матеріалу по темі «Трикутники», вивченого в 7-му класі. Завдання учням: переглянути слайди, пригадати теоретичний навчальний матеріал з даної теми, придумати кілька запитань по темі «Трикутники» до товаришів.

2. Друга сходинка - активне повторення + бліц-опитування

Учні однієї групи задають запитання, учні інших груп відповідають.

Бліц-опитування (запитання вчителя)

• Як називається відрізок, що сполучає вершину трикутника з серединою протилежної сторони?
• Який трикутник називається прямокутним ?
• Чи може в трикутнику бути два прямих кути ? Чому ?
• Що таке зовнішній кут трикутника ?
• Чому дорівнює зовнішній кут трикутника ?
• Як читається теорема про властивість рівнобедреного трикутника ?
• Чому дорівнює сума кутів трикутника ?
• Скільки ви знаєте ознак рівності трикутників ?
• Який трикутник називається  рівностороннім ?
• Що таке перпендикуляр, похила, проекція ?
• Які ви знаєте ознаки рівності прямокутних трикутників ?
• Що таке відстань від точки до прямої ?
• Що більше: гіпотенуза чи катет прямокутного трикутника ?

      Закінчити речення:

• Якщо дві сторони і кут між …
• У рівнобедреному трикутнику …
• Сума гострих кутів прямокутного …
• Якщо сторона і прилеглі до неї …
• Якщо три сторони одного трикутника …
• Катет прямокутного трикутника, що лежить проти …
• Якщо в трикутнику два кути рівні, то …
• Зовнішній кут трикутника дорівнює …
• У прямокутному трикутнику квадрат гіпотенузи …
• У кожному трикутнику проти більшої сторони …
• Кожна сторона трикутника менша …
• Два прямокутні трикутники рівні, якщо катети одного з них ….
• Сума кутів трикутника ….
• Сума зовнішніх кутів трикутника, взятих при кожній вершині по одному …
• У кожному трикутнику гіпотенуза довша …

3. Третя сходинка - усні вправи

1. Кут при вершині рівнобедреного трикутника дорівнює 20⁰. Знайти кут при основі цього трикутника.
2. Кути трикутника пропорційні до чисел 2, 3, 4. Знайти кути цього трикутника.
3. Гострий кут прямокутного трикутника дорівнює 10⁰. Чому дорівнює другий гострий кут цього трикутника ?
4. У рівнобедреному трикутнику основа дорівнює 15 см, а бічна сторона на 5 см менша. Знайти периметр цього трикутника.
5. У рівнобедреному трикутнику одна сторона дорівнює 4 см, друга сторона – 5 см. У скільки разів периметр цього трикутника більший за його основу ? Скільки випадків треба розглянути ?
6. Сторона рівностороннього трикутника дорівнює 10 см. Чому дорівнює периметр цього трикутника ?
7. Периметр рівностороннього трикутника дорівнює 40 дм. Чому дорівнює сторона цього трикутника ?
8. Що більше: периметр квадрата зі стороною 5 см чи периметр трикутника зі сторонами 10см, 5 см і 6 см ?

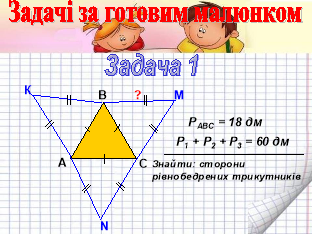
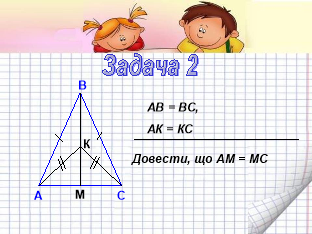
4. Четверта сходинка - задачі за готовим малюнком

На дошку проектується  малюнок та  короткий запис умови задачі. Протягом 30-40 секунд учні в групах обговорюють і знаходять ідею розв’язування задачі (задачу 1 розв’язують учні 1-ої і 2-ої групи, задачу 2 – учні 3-ої і 4-ої групи, задачу 3 розв’язуємо колективно. Групи працюють в режимі «демократії»)

 Відповідають представники кожної групи. При необхідгості учні інших груп доповнюють  або пропонують інший спосіб розв’язування задачі.

ІІІ. Контроль і самоперевірка знань та умінь

5. .  П’ята сходинка - тестові завдання

 1) Колективне розв’язування (на дошку проектуються тестові завдання та пропоновані відповіді. Учитель читає умову задачі, учні протягом 30 секунд думають, можуть обговорювати в групах   і повідомляють одержану відповідь. Якщо відповідь правильна, то перехід до «Правильно ! Молодці!», якщо відповідь неправильна, то перехід до «Подумайте ще…». Тоді знову повертаємося до завдання, яке було розв’язано неправильно)

Завдання:

1. Зовнішній кут при вершині рівнобедреного трикутника дорівнює 140⁰. Знайдіть внутрішній кут при основі цього трикутника.

А) 35⁰;            Б) 110⁰;         В)70⁰;        Г) 50⁰.

2.  У трикутнику АВС кут А дорівнює 25⁰, кут С на 10⁰ більший від кута А. Знайдіть кути В і С.

А) 120⁰; 35⁰;  Б) 110⁰; 35⁰;     В) 130⁰; 35⁰;    Г) 35⁰; 35⁰.

3. Периметр рівнобедреного трикутника дорівнює 50 см, а його бічна сторона – 17 см. Знайдіть основу трикутника.

А) 16,5 см;  Б) 17 см;  В) 16 см;  Г) 8 см.

4. Один із зовнішніх кутів трикутника дорівнює 120⁰, а один із внутрішніх кутів, не суміжних з ним, у 5 разів більший від іншого. Знайдіть градусну міру найменшого внутрішнього кута цього трикутника.

А) 24⁰;              Б) 20⁰;  В) 100⁰;  Г) 15⁰.

5. На якому з наведених малюнків правильно позначено градусні міри кутів ?

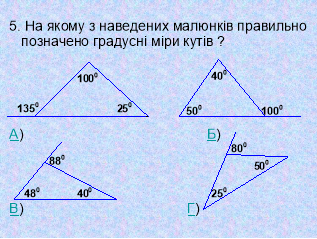
2) Індивідуальне розв’язування (13 учнів за комп’ютером виконують тестові завдання у програмі My Test, 13 учнів виконують тренувальні тестові завдання, заповнюють бланк відповідей)

Завдання:

1.  Кут при основі рівнобедреного трикутника дорівнює 70⁰. Знайти кут при вершині цього трикутника.

1) 50⁰;        2) 40⁰;           3) 140⁰;    4) 70⁰.

2. Периметр рівнобедреного трикутника дорівнює 12 см, бічна сторона 5 см. Чому дорівнює основа цього трикутника ?

1) 5 см;      2) 10 см;  3) 2 см;   4) 2,5 см.

3. Зовнішній кут при вершині рівнобедреного трикутника дорівнює 80⁰. Знайти кут при основі цього трикутника.

1) 40⁰;               2) 60⁰;  3) 100⁰;  4) 80⁰.

4. Внутрішні кути трикутника відносяться, як 1:2:3. Чому дорівнює найбільший кут цього трикутника ?

1) 30⁰;              2) 50⁰;  3) 120⁰;  4) 90⁰.

5. Гострий кут прямокутного трикутника дорівнює 48⁰. Знайти другий гострий кут цього трикутника.

1) 48⁰;        2) 60⁰;              3) 42⁰;  4) 130⁰.

6.  Один із кутів трикутника дорівню 40⁰, другий – на 20⁰ більший. Чому дорівнює третій кут цього трикутника ?

1)100⁰;       2) 80⁰;   3) 60⁰;   4)  120⁰.

7. Кути трикутника пропорційні до чисел 2, 3, 5. Чому дорівнює найменший кут цього трикутника ?

1) 30⁰;        2)54⁰;             3) 28⁰;     4) 36⁰.

8. Знайти периметр рівнобедреного трикутника, якщо його основа дорівнює 12 см, а бічна сторона на 5 см менша.

1) 26 см;          2) 84 см;  3) 38 см;  4) 24 см.

9.  Зовнішній кут при основі рівнобедреного трикутника дорівнює 110⁰. Чому дорівнює кут  при вершині цього трикутника ?

1) 70⁰;             2)110⁰;  3) 40⁰;    4) 100⁰.

IV. Застосування узагальнених знань у нових умовах

6. Шоста сходинка - образно-логічний диктант «Вірю - не вірю»

Учитель ставить до учнів класу  запитання.  Кожне запитання починається словами: «Чи вірите ви, що …»

Якщо учень вважає, що відповідь правильна, то піднімає праву руку, якщо неправильна, то – ліву руку  (бажано виконувати завдання із заплющеними очима, що сприяє відпочинку очей, а також розвиває образну уяву і мислення). Через одну хвилину змінюється завдання: якщо учні вважають відповідь правильною, то – «хлопок ладонями», якщо відповідь неправильна, то – тиша.

Запитання до класу:

Чи вірите ви, що…

1. … у рівнобедреному трикутнику кути при основі рівні ?
2. … у прямокутному трикутнику сума гострих кутів дорівнює 90⁰ ?
3. … кожний кут рівностороннього трикутника дорівнює 60⁰ ?
4. … існує трикутник, кути якого дорівнюють 90⁰, 80⁰, 10⁰ ?
5. … зовнішній кут трикутника завжди тупий ?
6. … висота рівнобедреного трикутника, проведена до основи, ділить трикутник на два рівні трикутники ?
7. … гіпотенуза трикутника довша за будь-який його катет ?
8. … існує трикутник зі сторонами 10 см, 5 см і 5 см ?
9. … існує трикутник,  дві висоти якого знаходяться за межами трикутника ?
10. … прямокутний трикутник може бути одночасно і рівностороннім ?
11.  … у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів ?

7. Сьома сходинка - сторінка цікавої математики

1. На екран проектується малюнок.

 Запитання:

а) Скільки всього трикутників зображено на малюнку ? (Відповідь: 10)

б) Скільки серед них рівнобедрених ? (Відповідь: 2)

в) Скільки на цьому малюнку прямокутних трикутників ? (Відповідь: 4)

2. Учні працюють в групах: «розрізати» рівносторонній трикутник на: а) два рівних трикутники; б) три рівних трикутники; в) чотири рівних трикутники; г) шість рівних трикутників; д) вісім рівних трикутників.

8. Восьма  сходинка - математичний кросворд

На екрані – кросворд. Звучить музика, діти дають відповіді на запитання кросворду.

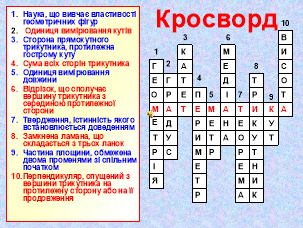
Запитання кросворду:

1. Наука, що вивчає властивості геометричних фігур.
2. Одиниця вимірювання кутів.
3. Сторона прямокутного трикутника, протилежна гострому куту.
4. Сума всіх сторін трикутника.
5.  Одиниця вимірювання довжини.
6. Відрізок, що сполучає вершину трикутника з серединою протилежної сторони.
7. Твердження, істинність якого встановлюється доведенням.
8. Замкнена ламана, що складається з трьох ланок.
9. Частина площини, обмежена двома променями зі спільним початком.
10. Перпендикуляр, опущений з вершини трикутника на протилежну сторону або на її продовження.

Ключове слово кросворду – математика.

І ми переходимо на останню сходинку: «Серенада математиці»

9.  Дев’ята сходинка – «Серенада математиці»

 Цю сторінку готують учні.

Звучить вірш про математику (автор Марія Будзінська, Хмельницька область)

Математика – кібернетика,

Математика – кораблі,

Математика – мова техніки,

Математика – рух Землі,

Математика – філософія,

Математика – зореліт,

Математика – мова Всесвіту,

Математика – це політ.

Математика – літочислення,

Математика – майбуття,

Математика – мова чисельна,

Математика – сприйняття.

Математика – око хімії,

Математика – відкриття,

Математика – мова істини,

Математика – це життя.

Розповідь учнів супроводжується презентацією.

Учень.  Математика – це не тільки формули, закони, графіки, але й люди, їхнє життя, почуття, доля. Кожен період історії математики багатий на видатних учених. Багато визначних математиків стали зразками патріотизму й щирої відданості науці.

Учениця  Олексій Григорович Івахненко…  -  академік Національної академії наук України, Заслужений діяч науки УРСР, двічі лауреат Державної премії України в галузі науки і техніки.

Учень.  Олексій Григорович – визначний учений в галузях автоматичного керування,  кібернетики та інформатики. Результати його досліджень отримали світове визнання. Але це визнання прийшло не автоматично, а завдяки принциповому і наполегливому відстоюванню правильності власної позиції.

Івахненко завжди доводив обгрунтованість своїх поглядів не тільки теоретично, а й реальними результатами – пристроями, діючими системами і розв’язанням конкретних прикладних задач. А такі докази, звичайно, не можна ні заперечити, ні відкинути, ні не визнати.

Учениця.  Народився Олексій Григорович Івахненко 30 березня 1913 року в місті Кобеляки Полтавської губернії.

Учень.  Батьки майбутнього академіка були дуже освіченими людьми. Його батько, Григорій Івахненко, працював учителем Кобеляцької чоловічої гімназії, мати, Марія Оперман – учителькою жіночої гімназії.

Учениця.  В 1922 році сім’я переїхала до Васильківа, що біля Києва. Тут Олексій  Івахненко навчався в семирічній школі, а після її закінчення поїхав навчатися в Київ.

Учень.  У 1932 році він закінчив Київський енерготехнікум, після чого два роки відпрацюва на Уралі. Він працював інженером на будівництві найбільшої Березняківської ТЕЦ.

Потім - навчання в Ленінградському електротехнічному інституті, робота в Москві у Всесоюзному  електротехнічному інституті,  у Києві в інституті будівельної механіки АН УРСР, в Інституті енергетики АН УРСР, в Київському політехнічному інституті, в інституті електротехніки АН УРСР. У 1954 році захистив докторську дисертацію.

Учениця.  О.Г. Івахненко опублікував близько 40 монографій і понад 700 статей. Багато його робіт перевидано англійською, німецькою, польською, болгарською, румунською і китайською мовами.

Протягом  усієї своєї творчої діяльності О. Г. Івахненко займався педагогічною роботою. Він читав лекції для студентів. Під його керівництвом виконано і успішно захищено близько 200 кандидатських дисертацій, до 20 його учнів захистили докторські дисертації та створили свої авторитетні наукові школи.

Учень.  Батьківщина високо оцінила його працю.

1953 рік – медаль «За трудовое отличие»,

1969 рік – медаль «За доблестный труд»,

1972 рік – звання «Заслужений діяч науки УРСР»,

1988 рік – орден «Дружби народів»,

1991 рік – Державна премія України,

1997 рік – Державна премія України

За визначний вклад у примноженні добра на Землі Олексій Івахненко нагороджений вищою відзнакою фонду міжнародних премій – орденом Миколи Чудотворця

Це  його нагороди за високі досягнення  в праці.

Учениця.  Олексій Григорович завжди говорив: «…Наука – це моє життя. Це те, чим я дихаю, заради чого живу на білім світі…»

Він був яскравим зразком ученого із загостреним почуттям нового і видатною науковою інтуїцією. До останніх днів свого життя він продовжував активно працювати, створювати оригінальні наукові ідеї та одержувати результати. Його по праву називають справжнім «невгамовним збурювачем спокою» і невичерпним генератором наукових ідей.

Учень.  Звичайно, наших знань ще дуже недостатньо, щоб зрозуміти його наукові праці, щоб розібратися в його наукових ідеях, щоб осягнути його всесвітньо визнаний метод МГУА – метод групового урахування аргументів.

Але ми гордимося, що людина такого високого злету – це наш земляк. І кожний з нас може багато  чому повчитися у цієї визначної  людини  – Олексія Григоровича Івахненка.

Учитель. Як ви думаєте:  які саме риси, притаманні  Олексію Григоровичу Івахненку,  вже сьогодні може формувати в собі кожний семикласник ? Чого саме ми можемо повчитися у цього видатного вченого ? (учні висловлюють свої думки)

То ж бажаю кожному навчитися  ставити перед собою чітку мету і цілеспрямовано та  наполегливо рухатися до її досягнення,

А «…коли людина постійно рухається до своєї мети, шукаючи при цьому своє місце в житті і роботі, не розгублюючись перед прикрими несподіванками, успіх їй гарантований» (Олексій Григорович Івахненко)

V. Підсумок уроку.

От наш урок і добігає кінця. Ми успішно піднялися сходинками до самої вершини, повторивши при цьому ввесь вивчений навчальний матеріал про трикутники.

- Які сходинки вам вдалися найлегше ?

- На яких сходинках було найцікавіше ?

- А які сходинки викликали затруднення ? (діти висловлюють свої враження, аналізуючи виконані завдання)

VI. Інформація про домашнє завдання.

Методичний прийом «Безпрограшна лотерея» (діти дістають зі скриньки номери задач, які потрібно розв’язати вдома, один учень дістає завдання для свого ряду) Задачі № 746, 767, 770.  Геометрія, 7 – підручник для 7 класу загальноосвітніх навчальних закладів, Г.П. Бевз, В.Г.Бевз, Н.Г. Владімірова