Конспект заняття з дисципліни «Технічна механіка» на тему: «КРУЧЕННЯ»
ВП НУБіП «Немішаївський агротехнічний коледж»
Конспект заняття з дисципліни
«Технічна механіка» на
тему: «КРУЧЕННЯ»
Для студентів спеціальності
208 «Агроінженерія» ІІ курсу денної форми навчання
|
|
|
Викладач: Лоїк О.А.
Немішаєве 2020
Кручення
План заняття
- Крутний момент. Побудова епюр крутних моментів.
- Кручення прямого бруса круглого поперечного перерізу. Напруження в поперечному перерізі бруса.
- Кут закручування. Полярні моменти опору для круга і кільця.
- Розрахунки на міцність і жорсткість при крученні.
- Розрахунок циліндричних гвинтових пружин розтягу і стиску з малим кроком витка.
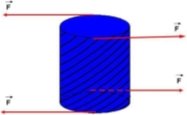
Крученням називають такий вид деформації, за якого в будь-якому поперечному перерізі бруса виникає тільки крутний момент. Деформації кручення виникають, якщо до прямого бруса в площинах, перпендикулярних до осі, прикладено пару сил. Моменти цих пар називають обертальними (якщо брус обертається) і скручувальними (якщо брус не обертається). Згідно зі стандартом, обертальний момент позначають Т.
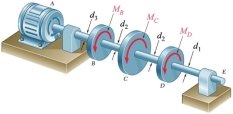
Розповсюдженим стержневим елементом конструкцій машин, що працюють на кручення, є вал. Якщо навантаження на прямолінійний стержень (вал) складається тільки з моментів Mк, площини дії яких перпендикулярні до осі стержня, то із шести зусиль та моментів у довільному перерізі залишається лише один – крутний момент.
Відзначимо, що найчастіше зовнішній крутний момент виникає у валах, що обертаються з кутовою швидкістю n [об./хв.] та передають потужність K [кВт] (розподільні, передавальні вали зубчатих, пасових передач). У цьому випадку на валу в місцях посадки зубчатих коліс, шківів виникає зосереджений крутний момент, [кH м]
![]()
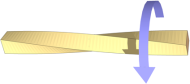
Деформа́ція кру́чення — вид деформації у вигляді повороту поперечних перерізів стрижня навколо його осі на деякий кут під дією у цих же перерізах крутного моменту.
|
|
|
|
|
|
Оскільки на кручення працюють вали, що звичайно мають круглий, або кільцевий переріз, то розглянемо кручення круглого циліндра рис. 1.
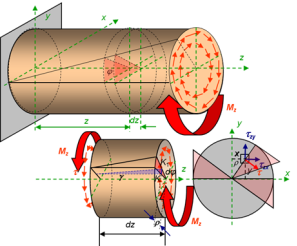
Рис. 1
Під час випробування гумового прямого кругового циліндричного бруса видно, що:
1) вісь циліндра, яку називають віссю кручення, залишиться прямолінійною;
2) діаметри кіл, під час деформації залишаться такими самими і відстань між колами не зміниться;
3) усі твірні циліндра повертаються на той самий кут;
4) кожний поперечний переріз повертається відносно один одного на деякий кут, який називають кутом закручування.
З цього можна зробити висновок, що для кручення круглого циліндра справедлива гіпотеза плоских перерізів, а також припустити, що радіуси кіл залишаються прямими під час деформації.
Кут φ повороту кінцевого перерізу називають повним кутом закручування.
Відносним кутом закручування називають відношення кута закручування до відстані цього перерізу від закріплення ![]() .
.
Під час кручення виникає деформація зсуву, але не за рахунок поступального, а як результат обертального руху одного поперечного перерізу відносно іншого. Отже, під час кручення у поперечних перерізах виникають тільки дотичні внутрішні сили, які утворюють крутний момент. Крутний момент є результуючим моментом відносно осі бруса внутрішніх дотичних сил, які діють у поперечному перерізі.
Для наочного зображення розподілу крутних моментів уздовж осі бруса будують епюри крутних моментів. Крутний момент у перерізах бруса визначають за допомогою методу перерізів. Побудова епюр крутних моментів ґрунтується на тому, що внутрішній крутний момент у даному перерізі чисельно дорівнює алгебраїчній сумі зовнішніх моментів відносно осі стержня усіх сил, розташованих по один бік від перерізу. Якщо вал обертається рівномірно, то алгебраїчна сума всіх моментів дорівнює нулю. Тому при визначенні Mк матимемо один і той самий результат, незалежно від того, чи будемо брати суму моментів, розташованих ліворуч або праворуч від перерізу.
Правило знаків: крутний момент вважається додатним, якщо при спостеріганні з торця вздовж осі частини, що розглядається, він намагається обертати розглянуту область (відсічену частину) проти годинникової стрілки і навпаки.
Сформулюємо правила для побудови і перевірки правильності епюр крутних моментів: 1.При побудові епюр варто перевіряти рівновагу вала, тобто ![]() 2.На ділянці з інтенсивністю розподіленого моменту m = const епюра Mк лінійна, а якщо m = 0 , то епюра Mк по довжині вала є кусочно-постійною по ділянках вала, тобто Mкi = const .
2.На ділянці з інтенсивністю розподіленого моменту m = const епюра Mк лінійна, а якщо m = 0 , то епюра Mк по довжині вала є кусочно-постійною по ділянках вала, тобто Mкi = const .
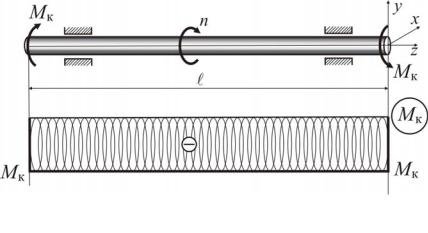
3. У точці прикладення зосередженого моменту на епюрі Mк спостерігається стрибок на величину зовнішнього моменту.
Епюри крутних моментів дають змогу визначити небезпечні перерізи.
Знаючи, що під час кручення відбувається деформація зсуву, природно вважати, що в точках поперечного перерізу бруса виникають тільки дотичні напруги.
На рис. 1 видно, що абсолютний зсув характеризується кутом зсуву γ.
Через незначні деформації ![]()
Оскільки радіуси поперечних перерізів під час деформації залишаються прямими, виразимо довжини дуг ![]()
де: φ – повний кут закручування, рад;
r – радіус циліндра;
ρ – відстань волокна b від осі кручення.
Розділимо![]() звідси
звідси ![]() кут зсуву прямо пропорційний відстані ρ до осі обертання.
кут зсуву прямо пропорційний відстані ρ до осі обертання.
Застосовуємо формулу закону Гука для зсуву
![]() за
за ![]()
дотичні напруги в поперечному перерізі змінюються за довжиною радіуса за лінійним законом.
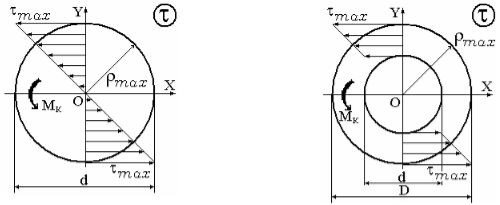
Рис. 2
Отже, дотичні напруги у кожній точці поперечного перерізу вала прямо пропорційні відстані ρ цієї точки від центра перерізу.
Графічно закон зміни дотичних напруг зображують прямою лінією. Епюру дотичних напруг показано на рис. 2. Як бачимо, найбільше значення дотичні напруги мають біля поверхні вала, в центрі вони дорівнюватимуть нулю.
Величину дотичної напруги після того, як знайдено закон розподілу, можна визначити з рівняння, яке виражає умову рівноваги відсіченої частини вала.
Сумарний момент усіх внутрішніх дотичних сил відносно осі вала дорівнює:![]()
де: dA – площа елементарної площадки на відстані ρ від осі кручення;
![]() – полярний момент інерції перерізу.
– полярний момент інерції перерізу.
![]() ;
;
![]() – формула для визначення дотичних напруг під час кручення бруса круглого поперечного перерізу.
– формула для визначення дотичних напруг під час кручення бруса круглого поперечного перерізу.
Коли ρ = r, то напруги матимуть максимальні значення.
![]() – полярний момент опору крученню (відношення полярного моменту інерції до радіуса перерізу).
– полярний момент опору крученню (відношення полярного моменту інерції до радіуса перерізу).
![]() – формула для визначення найбільших дотичних напруг.
– формула для визначення найбільших дотичних напруг.
![]() – формула для визначення відносного кута закручування, рад.
– формула для визначення відносного кута закручування, рад.
![]() – формула для визначення повного кута закручування, рад/м.
– формула для визначення повного кута закручування, рад/м.
![]() – жорсткість перерізу під час кручення.
– жорсткість перерізу під час кручення.
У формулах кут закручування виражено в радіанах. Переведення у градуси виконується за такою формулою: ![]() .
.
Повний кут закручування круглого циліндра прямо пропорційний крутному моменту, довжині циліндра і обернено пропорційний жорсткості перерізу під час кручення.
Оскільки для виведення формули застосовано закон Гука, то вона дійсна в межах, коли навантаження і деформація прямо пропорційні.
Для циліндричного бруса, який має кілька ділянок, які різняться матеріалом, розмірами поперечного перерізу, величиною крутного моменту, повний кут закручування дорівнює алгебраїчній сумі кутів закручування окремих ділянок.
Полярні моменти інерції і моменти опору перерізу вала.
Для суцільного круглого вала:
![]() .
.
![]() де
де ![]()
Умова міцності бруса для кручення полягає у тому, що найбільша дотична напруга, яка виникає у ньому, не має перевищувати допустиму. Розрахункова формула на міцність для кручення має вигляд:
![]() .
.
Крім міцності до валів ставлять вимогу жорсткості, яка полягає у тому, що кут закручування 1м довжини вала не має перевищувати певної величини, щоб не сталося, наприклад, пружинення валів або втрат точності ходових гвинтів токарно-гвинторізних верстатів. Не можна допускати великих кутів закручування в зубчастих передачах за великих кутів закручування вали зубчастих коліс перекосяться. Це призводить до кришення поверхні зубів і поломки передачі.
Допустимий кут закручування 1м довжини вала задають у градусах і позначають ![]() ; розрахункова формула на жорсткість для кручення має вигляд:
; розрахункова формула на жорсткість для кручення має вигляд:
.
![]()
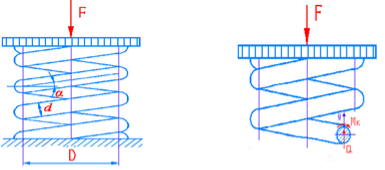
Розглянемо приклад інженерного розрахунку гвинтових циліндричних пружин, які поширені у техніці (ресорах вагонів, клапанах, інших механізмах сучасних транспортних засобів).
Розглянемо пружину, виготовлену зі стального круглого прутка; ![]() – осідання пружини під дією сили F. Розрахункові параметри:
– осідання пружини під дією сили F. Розрахункові параметри:
d – діаметр прутка; D– середній діаметр витків; n – кількість витків.
Згідно з методом перерізів, розглядаючи рівновагу верхньої частини пружини, визначаємо внутрішні силові фактори: поперечну силу Q=F та крутний момент![]() . Звідки випливає, що у поперечному перерізі витка діють тільки дотичні напруження зсуву та кручення.
. Звідки випливає, що у поперечному перерізі витка діють тільки дотичні напруження зсуву та кручення.
Насправді, при цьому ми нехтували малими за величиною подовжньою силою та згинальним моментом. Помилка за такого розрахунку буде більшою, що більше кут піднімання витка α.
Максимальні сумарні напруження діють у крайній точці перерізу витка на внутрішньому радіусі пружини:
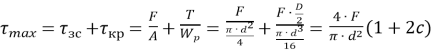
де ![]() – індекс пружини.
– індекс пружини.
Аналіз свідчить, що напруження зсуву ![]() становлять лише 5–10 % від напружень кручення
становлять лише 5–10 % від напружень кручення![]() і можуть за грубих розрахунків не враховуватися.
і можуть за грубих розрахунків не враховуватися.
Більш точний результат дає формула, яка враховує кривизну витків за допомогою спеціального поправкового коефіцієнта![]() ;
;
тоді формулу для розрахунку пружини на міцність можна записати у вигляді:
![]() .
.
Під час визначення осідання f пружини будемо враховувати тільки кручення витого прутка, бо інші види деформування вносять дуже малий вклад. Скористаємось енергетичним підходом, згідно з яким робота зовнішньої сили F на осіданні f переходить у потенційну енергію U деформованої пружини, яка дорівнює роботі крутного моментуTx на куті ![]() закручення прутка .
закручення прутка .
Запишемо потенційну енергію U з урахуванням формули для ![]() , величини крутного моменту
, величини крутного моменту ![]() , довжини прутка
, довжини прутка ![]() та формули для Ip :
та формули для Ip :
![]()
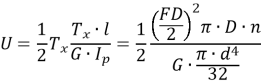
Після підставлення виразів для ![]() і U та деяких скорочень отримаємо остаточну розрахункову формулу для осідання пружини:
і U та деяких скорочень отримаємо остаточну розрахункову формулу для осідання пружини:
.
![]()
Можна підібрати такі параметри пружини, щоб отримати для заданого навантаження бажане осідання пружини.
Література:
1. Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655с.
2. Опір матеріалів. Конспект лекцій. Мильніков О.В.− Тернопіль: Видавництво ТНТУ, 2010. − 257 с.


про публікацію авторської розробки
Додати розробку