Конспект "Застосування інтеграла до розв'язування прикладних задач"

Клас: 11

Предмет: Алгебра і початки аналізу

Тема уроку: Застосування інтеграла до розв'язування прикладних задач

Мета: поглибити і розширити знання учнів про визначений інтеграл, продовжити формування навичок знаходити визначений інтеграл, показати його місце і значення під час розв’язування задач геометричного та фізичного змісту. Сприяти розвитку творчих здібностей учнів, формувати їх пізнавальний досвід, вміння виступати перед аудиторією. Розвивати логічне мислення, інтелектуальні здібності учнів. Виховувати інтерес до науки, вміння раціонально використовувати робочий час.

Тип уроку: засвоєння знань

Хід уроку

І. Організаційний момент

ІІ. Актуалізація опорних знань

Перевірка й повторення базових знань «Розминка».

      А зараз відповідаючи на запитання вікторини «Що? Де? Чому?»,  ми налаштуємось на розгляд більш складних проблем.

Питання:

1. Що таке первісна?
2. Сформулювати основну властивість первісної;
3. Чому дорівнює значення визначеного інтеграла на відрізку [a;b]?
4. Назвіть формулу Ньютона-Лейбніца.
5. Дайте означення криволінійної трапеції.
6. Як знайти площу криволінійної трапеції? Об`єм?

ІІІ. Оголошення теми і мети уроку

    Визначений інтеграл застосовується не тільки для знаходження площ фігур і об’ємів тіл обертання, а також для знаходження відстані, роботи змінної сили, обчислення маси, кількості електрики. Визначений інтеграл застосовується навіть в економіці.

Тому сьогодні ми будемо вчитися розв’язувати задачі прикладного змісту за допомогою визначеного інтеграла.

Тема уроку «Застосування інтеграла до розв'язування прикладних задач»

А де саме визначений інтеграл застосовується у фізиці?

Давайте розглянемо, коли нам може знадобитися визначений інтеграл при розв’язуванні задач з економіки?

Якщо f(t) – продуктивність праці в момент t, то = – обсяг продукції, яка випускається за проміжок часу [0; T].

Приклад. Продуктивність  праці  робітника протягом дня задається функцією z(t) = – 0,00645t² + 0,05t + 0,5 (грош. од./год), де t – час в годинах від початку роботи, 0 ≤ t ≤ 8. Знайти функцію   яка показує обсяг продукції (у вартісному виразі) та його величину за робочий день.

Розв’язання:

ІV. Історична довідка про визначений інтеграл.

Поняття інтеграла пронизую всю сучасну математику. Варто розкрити будь-яку книгу, що відноситься до точних наук, як зустрінеться знак інтеграла. Більш того, останнім часом увійшли до ужитку такі терміни, як, наприклад «інтегральна схема», «економічна інтеграція», які прямого відношення до інтеграла не мають, але смислове навантаження зберігають.

Інтегральне та диференціальне числення – це числення нескінченно великих або нескінченно малих величин, які перебувають в русі. Початки інтегральних методів простежуються в працях Архімеда, Евдокса Кнідського, Зенона Елейського. У книгах по історії математики відповідні розділи так і називаються – «Інтегральні методи Архімеда». Для переходу від методів Архімеда до алгоритму інтегрального числення математика повинна була пройти довгий шлях, на якому була створена буквенна символіка, побудовано вчення про функціональні залежності, розроблений аналітичний апарат для їх виразу.

Вдосконалення методів Архімеда і створення інтегрального числення, його розвиток здійснювалися в роботах Кеплера, Паскаля, Ферма, Ньютона, Лейбніца, Братів Бернуллі, Ейлера, Коші та інших видатних математиків.

Символ інтеграла введений Лейбніцом. Цей знак є змінною латинською буквою S. Слово інтеграл (латинського походження) придумав  Яков Бернуллі. Винайдення інтегрального і диференціального числення – це великий стрибок у розвитку людства, яким захоплювалося не одне покоління математиків.

       А зараз перейдемо до застосування визначеного інтеграла для розв’язування прикладних задач фізичного змісту.

Кожна група одержала завдання підготувати прикладні задачі, розв’язання яких потребує застосування визначеного інтеграла. Прошу учнів І групи.

V. Застосування визначеного інтегралу

Робота біля дошки

№1 Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом v = 2t + 1 (м/с). Знайти шлях, який пройшло тіло за інтервал часу від t₁ = 1 с до t₂ = 3 с.

Розв’язання

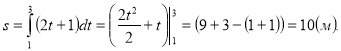
Відповідь: s = 10 м.

№2 Знати масу стержня завдовжки 35 см, якщо його лінійна густина змінюється за законом

Розв’язання

Відповідь: m = 1,3 кг.

№3 Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом

Розв’язання

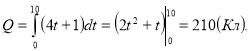
Відповідь: Q = 210 Кл.

VІ. Робота в групах

Математика – потужна зброя в руках фізика, економіста. Адже багато наслідків можна одержати математично, використовуючи перевірені дослідом формули. Зараз ви  покажете, як можна використати цю зброю. Давайте перенесемося в майбутнє, років на 15 вперед. Ви – дорослі, солідні люди, знайшли своє місце в житті: конструктори, інженери, металурги, будівельники, економісти, плановики, вчені. І в процесі своєї роботи ви зустрічаєтеся з різними проблемами, які вам необхідно вирішити.

Розіб’ємо клас на 5 груп, кожна з яких отримує певне завдання і через 5 хвилин звітує про виконану роботу.

Фінансисти  На  полі   пшениці  після   приземлення космічного корабля  залишився  слід,    який   нагадує     фігуру,     обмежену    лініями    у =‌‌‌‌‌ х² – 2х - 8     та     у = 2+ х. Необхідно визначити збитки, завдані агрокомплексу, якщо з 1 м² отримують в середньому 3,8 кг пшениці, яка коштує  1 грн. / кг.

Археологи Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = –  х² + 2х + 3 навколо вісі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м³. Яка масу каменя використали на виготовлення цього жертовника стародавні майстри?

Розв’язання.

Побудуємо фігуру, обмеженою параболою у = –  х² + 2х + 3,  вісями Оу та Ох.

V =  .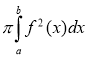

= =

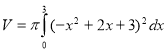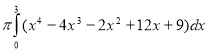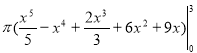= = 3,14(48,6 – 81 – 18 + 54 + 27) =

= 3,1430,6 = 96,084 (м³)

Відповідь. 240210 кг.

Фізики Для кращого обслуговування заїзду гонок серії „Формула-1” майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 2·(t+2)^5/2. Який шлях проїде пілот цієї гонки за 7 с від початку руху? Який шлях він проїде за сьому секунду?

Розв’язання:

= = 1243 (м)

=  = = 422 (м)

Відповідь 1243 м; 422 м.

Біологи  Знайти площу пелюстка ромашки, який розміщено  між дугами парабол у=х² та у=.

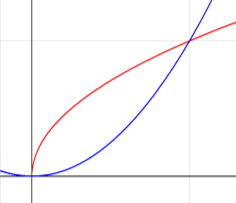
Дана фігура обмежена графіками двох функцій: у=х² та у=. Шукана площа за допомогою інтеграла обчислюється так:

S = 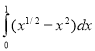= = 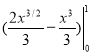– = (кв. од.)

Відповідь. кв. од.

Енергетики Навантаження    на   Слов’янську теплоелектростанцію     задається     функцією    N(x) = 3x² + 4x – 2. Визначити витрати електроенергії протягом доби.

Розв’язання:

А=( кВт·год)

Відповідь: 14343 кВт·год.

VІІ. Підведення підсумків

За посиланням дайте відповіді на запитання кросворду http://surl.li/jsogk

Питання до кросворду

1. Першу букву якого слова  нагадує знак інтеграла? (Сума)
2. Хто з відомих математиків-фізиків дослідив  фізичний зміст інтеграла? (Ньютон)
3. Хто з відомих математиків дослідив геометричний зміст інтеграла? (Лейбніц)
4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? (криволінійна)
5. Як називається функція, яка стоїть під знаком інтеграла? (підінтегральна)
6. Як називається множник dx у підінтегральному виразі? (диференціал)
7. Як називається операція обернена до операції диференціювання? (інтегрування)

VІІІ. Домашнє завдання

Опрацювати: параграф 12 за підручником О. Істер «Математика» http://surl.li/akxqc

 Розв’язати: 4 задачі на вибір із запропонованих.

№1 Знайти масу неоднорідного стержня завдовжки 30 см, якщо його лінійна густина змінюється за законом

№2 Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом

№3 Відомо, що попит на деякий товар задається функцією де q – кількість товару (шт.), р – ціна за одиницю товару (грн.), а рівновага на ринку даного товару досягається при р = q = 1. Визначте величину споживацького надлишку.

№4 Обчислити роботу, яку треба виконати, щоб розтягнути пружину на 0,06 м, якщо сила 12 Н розтягує її на 0,01 м.

В к а з і в к а. За законом Гука, сила F пропорційна розтягуванню або стисканню пружини, тобто F = kx, де  х – величина розтягування або стискання. З умови задачі можна знайти k. Оскільки при х = 0,01 м сила F дорівнює 12 Н, то Отже, F = kx = 1200x.

№5 Тіло рухається прямолінійно зі швидкістю v(t) (м/с). Обчислити шлях, пройдений тілом за інтервал часу від t₁ до t₂, якщо

№6 Обчислити роботу, яку треба виконати, щоб викачати  воду з циліндричної цистерни, радіус якої дорівнює R, а висота – Н.