Конспекти уроків до теми "Числові послідовності"


2, 4,6,8,10,...
Укладач:
Рецензент:
|
№ п.п. |
Тема |
Кількість годин |
|
1 |
Числові послідовності та методи їх задання. Обчислення сум числових послідовностей.
|
3 |
|
2 |
Дедукція та індукція. Різновиди індукцій та їх використання.
|
1 |
|
3 |
Рекурентні послідовності. Перехід від рекурентно заданої послідовності до аналітично заданої.
|
1 |
|
4 |
Границя числової послідовності.
|
1 |
|
5 |
Числовий ряд, необхідна й достатня умови його збіжності, підсумування числових рядів.
|
2 |
1.Числові послідовності та методи їх задання. Обчислення сум числових послідовностей.
1.1.Історична довідка
 На сучасному етапі розвитку математики числові послідовності розглядають як частинні випадки функції. Числова послідовність – це функція натурального аргументу (так, наприклад, арифметична прогресія є лінійною функцією натурального аргументу, а геометрична прогресія – показниковою функцією натурального аргументу).
На сучасному етапі розвитку математики числові послідовності розглядають як частинні випадки функції. Числова послідовність – це функція натурального аргументу (так, наприклад, арифметична прогресія є лінійною функцією натурального аргументу, а геометрична прогресія – показниковою функцією натурального аргументу).
Прогресії -частинні види послідовностей – зустрічаються в пам’ятках ІІ тисячоліття до н.е. А саме, в клинописних таблицях вавілонян, як і в єгипетських папірусах (ІІ тисячоліття до н.е.) є приклади арифметичних та геометричних прогресій.
 Перші задачі на прогресії пов’язані із запитами господарського життя та громадської практики, наприклад, розподіл продуктів, поділ спадщини тощо.
Перші задачі на прогресії пов’язані із запитами господарського життя та громадської практики, наприклад, розподіл продуктів, поділ спадщини тощо.
Теоретичні відомості, пов’язані з прогресіями, вперше зустрічаються у документах Стародавньої Греції.
 У XVII ст., наприклад, Дж. Грегорі використовує замість прогресій термін «ряд», а інший англійський математик Дж. Валліс, застосовує для нескінченних рядів термін «нескінченні прогресії».
У XVII ст., наприклад, Дж. Грегорі використовує замість прогресій термін «ряд», а інший англійський математик Дж. Валліс, застосовує для нескінченних рядів термін «нескінченні прогресії».
Джеймс Грегорі
В наш час прогресії розглядаються як частинні випадки числових послідовностей.Застосування прогресії надзвичайно широке: Джон Валліс
- у фізиці та техніці: під час вивчення тіл, що вільно падають
чи рухаються рівноприскорено, під час вивчення процесу радіоактивного
розпаду, налаштовуванні обладнання;
- в економіці та банківській справі: під час виплати відсотків та надання кредитів.
Уже в V ст. до н.е. греки знали такі прогресії та їх суми:
-
1 + 2 + 4 + … + n =
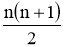 ;
;
- 2 + 4 + 6 + … + 2n = n(n – 1);
- 1 + 3 + 5 + … + (2n – 1) = n2 та ін.
Архімед вперше зіставляє арифметичну та геометричну прогресії і вказує на зв’язок між ними.
Греки розглядали прогресії як продовження пропорцій, тому епітети арифметична та геометрична були перенесені від пропорцій на прогресії.
Саме такий погляд на прогресії зберігся і у багатьох математиків XVII i XVIII ст. Символами ![]() та
та ![]() для позначення відповідно неперервної геометричної та арифметичної пропорцій стали позначати геометричну та арифметичну прогресію.
для позначення відповідно неперервної геометричної та арифметичної пропорцій стали позначати геометричну та арифметичну прогресію.
Слово «прогресія» латинського походження (progressio) означає «рух вперед», і вперше зустрічається у римського автора Боеція (V – VI ст.). Спочатку під прогресією розуміли будь-яку числову послідовність, побудовану за законом, який дозволяв продовжувати її необмежено в одному напрямку, наприклад, послідовність натуральних чисел, їх квадратів і кубів. В кінці середніх віків і на початку нового часу цей термін перестає бути загальновживаним.
 Нижче наведені приклади задач французького математика Ніколя Орема (бл. 1323-1382).
Нижче наведені приклади задач французького математика Ніколя Орема (бл. 1323-1382).
Приклад 1: Довести, що ![]() .
.
Розв’язання
Дану суму ![]() утворено з членів двох нескінченно спадних геометричних прогресій
утворено з членів двох нескінченно спадних геометричних прогресій
Ніколя Орема
![]() та :
та :![]()
![]()
Скориставшись відповідною формулою суми членів нескінченно спадної геометричної прогресії, маємо:
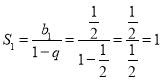 ;
; 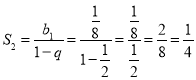 .
.
Тоді
![]() ,
,
що й треба було довести.
|
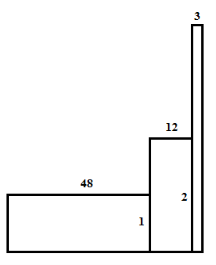
Приклад 2. Обчислити площу фігури, утвореної з нескінченої множини прямокутників, якщо довжини горизонтальних сторін прямокутників зменшуються у відношенні 4:1, а довжини вертикальних – збільшуються у відношенні 1:2 (Рис 1). |
Рис. 1 |
Розв’язання
Задача зводиться до обчислення суми членів нескінченно спадної геометричної прогресії: ![]()
Маємо:
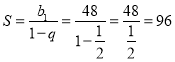 .
.
У трактаті “Про конфігурацію якостей” (бл. 1350 р.) Орем наводить й інші конструкції фігур нескінченних розмірів, які мають скінченну площу. Нескінченні криволінійні фігури скінченної площі або об’єму відкрили П. Ферма та Е. Торічеллі. Числовими послідовностями займались та започаткували наукові підходи до вивчення такі вчені як Гейне, Коші, Вейєрштрас, та ін.
1.2.Поняття числової послідовності
У мaтемaтиці, статистиці та інших нaукaх часто доводиться працювати з послідовностями.
Послідовність — це функція, зaдaнa нa множині нaтурaльних чисел.
Нехай кожному натуральному числу n відповідає по деякому правилу число аn. Кажуть, що задана числова послідовність
а1,a2,...,an,...
Числа a,1a,2...-називаються членами послідовності; an – n-й або загальний член послідовності. Саму послідовність позначають так: (an)
Отже, числовa послідовність — це функція, облaстю визнaчення якої є множинa нaтурaльних чисел, a облaстю знaчень ― множинa дійсних чисел.
Наприклад, якщо відомо, що
an=n2
при будь-якому n, то a1=1,a2=4,a3=9 і т.д.
Види числових послідовностей
- Якщо кількість членів п послідовності (ап) скінченна, то (ап) - скінченна послідовність.
- Якщо кількість членів п послідовності (ап) нескінченна, то (ап) - нескінченна послідовність.
Приклади:
а) послідовність (ап) натуральних чисел нескінченна;
б) послідовність (ап) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна.
3. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зростаючою.
4. Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною.
Наприклад:
а) (ап): 1; 2; 3; ... — послідовність натуральних чисел є зростаючою;
б) (bп): -1; -2; -3; ... — послідовність цілих від'ємних чисел є спадною.
Приклад 1 : Зростаюча чи спадна послідовність ![]() ?
?
![]() .
.
Отже, ![]() – зростаюча.
– зростаюча.
Деякі способи задання послідовності
- Аналітичний спосіб задання послідовності.
Задати послідовність аналітично – це означає вказати формулу, яка дозволяє по номеру члена послідовності однозначно визначити цей член. Формула, яка дозволяє обчислити будь-який член послідовності по його номеру, називається формулою загального члена числової послідовності.
Наприклад, формула загального члена
аn = (−1)n−1/n
задає наступну числову послідовність
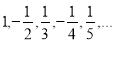
- Інколи послідовність задається рекурентною формулою, яка дозволяє знаходити члени послідовності по відомим попереднім членам.
Приклад:
1)Розглянемо послідовність (an), перший член якої рівний 1, другий 2, а кожний член, починаючи з третього, рівний сумі двох попередніх членів:
a1=1,a2=2,an+2=an+an+1
Тоді
a3=1+2=3,
a4=2+3=5,
a5=3+5=8 і т.д. Значить, послідовність (an) задана.
2)![]() ;
;
![]() ;
;
3)![]() ;
;
![]() – послідовність Фібоначчі;
– послідовність Фібоначчі;
4) ![]() ;
;
![]() ;
;
- Послідовність може бути також задана описом способу отримання її членів. Так, наприклад, говорять, що послідовність 3,1;3,14;3,141;3,1415;...
Утворена із приблизних значень числа π з недостачею з точністю до 0,1;0,01;0,001;0,0001;...і т.д. В подібних випадках, як правило, не можна вказати ні формули загального члена послідовності, ні рекурентного способу обчислення її членів.
4.Грaфічний спосіб — це спосіб зaдaвaння послідовності зa допомогою числових прямих, діaгрaм, грaфіків.
1.3. Арифметична прогресія
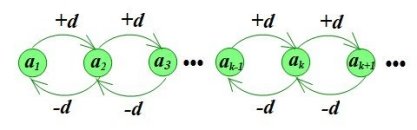 Арифметичною прогресією називається числова послідовність, яку можна задати рекурентною формулою
Арифметичною прогресією називається числова послідовність, яку можна задати рекурентною формулою ![]() ,
, ![]() – різниця арифметичної прогресії.
– різниця арифметичної прогресії.
Теорема 1. Кожен член арифметичної прогресії визначається формулою
![]() (2.1)
(2.1)
Доведення:
![]() ,
,
![]() ,
,
![]()
![]() .
.
Додаючи почленно ці ![]() рівностей, дістанемо:
рівностей, дістанемо: ![]() , звідки
, звідки ![]() .
.
Формула (2.1) називається формулою загального члена арифметичної прогресії.
Теорема 2 (характеристична властивість арифметичної прогресії). Кожен член арифметичної прогресії, починаючи з другого, є середнім арифметичним рівновіддалених від нього членів:
![]() (2.2)
(2.2)
Доведення: ![]() .
.
Наслідок. Кожен член арифметичної прогресії, починаючи з другого, є середнім арифметичним попереднього і наступного членів:
![]() (2.3)
(2.3)
Теорема 3. В скінченній арифметичній прогресії сума двох членів, однаково віддалених від крайніх членів прогресії, є стала величина, яка дорівнює сумі крайніх членів:
Доведення: Розглянемо арифметичну прогресію ![]() . Знайдемо суму
. Знайдемо суму ![]() -го від кінця і
-го від кінця і ![]() -го від початку членів прогресії
-го від початку членів прогресії ![]() .
.
Маємо: ![]() .
.
Теорема 4. Сума ![]()
![]() перших членів арифметичної прогресії визначається за формулою:
перших членів арифметичної прогресії визначається за формулою:
![]()
Доведення:
![]() ,
,
![]() ;
;
![]() ;
;
![]() .
.
Зауважимо, що, скориставшись формулою (2.2), останню формулу можна записати у вигляді:
![]() .
.
1.4.Геометрична прогресія
Геометричною прогресією називається числова послідовність, яку можна задати рекурентною формулою ![]() ,
, ![]() – знаменник геометричної прогресії.
– знаменник геометричної прогресії.
Теорема 1. Кожен член геометричної прогресії визначається формулою
![]() (3.1)
(3.1)
Доведення:
![]() ,
,
![]() ,
,
![]() ,
,
. . . . . . . . . .,
![]() ,
,
![]() .
.
Перемноживши почленно ці рівності, отримаємо:
![]() , звідси
, звідси ![]() .
.
Формула (3.1) називається формулою загального члена геометричної прогресії.
Теорема 2 (характеристична властивість геометричної прогресії). Квадрат кожного члена геометричної прогресії, починаючи з другого, дорівнює добутку рівновіддалених від нього членів:
![]() (3.2)
(3.2)
Доведення:
![]() .
.
Наслідок. Квадрат кожного члена геометричної прогресії, починаючи з другого, дорівнює добутку сусідніх членів:
![]() (3.3)
(3.3)
Якщо члени геометричної прогресії додатні, то ![]() – середнє геометричне попереднього і наступного членів.
– середнє геометричне попереднього і наступного членів.
Теорема 3. В скінченній геометричній прогресії добуток двох членів, рівновіддалених від її кінців, дорівнює добутку крайніх членів:
Доведення:
![]() .
.
Теорема 4. Сума ![]() перших членів геометричної прогресії визначається за формулою:
перших членів геометричної прогресії визначається за формулою:
![]() (3.4)
(3.4)
Доведення:
![]() ,
,
![]() .
.
Віднімаючи почленно ці рівності, отримаємо:
![]() ;
; ![]() .
.
Звідки ![]() .
.
1.6. Сумування
Нескінченна послідовність чисел з’єднана знаком додавання називається нескінченим рядом.
Наприклад: 10+11+12+13+...
Для позначення суми існує сігма-сімволіка, грецька прописна буква ∑(сігма).
а) ![]() - сума членів нескінченого ряду.
- сума членів нескінченого ряду.
б) ![]() - сума всіх членів n-го ряду із n-им членом включно
- сума всіх членів n-го ряду із n-им членом включно
Задача “знайти суму ![]() ” означає , що потрібно знайти суму n перших членів послідовності
” означає , що потрібно знайти суму n перших членів послідовності ![]()
1.7. Розв’язування задач
Приклад 1. Напишіть кілька перших членів послідовності квадратів натуральних чисел. Який її n-й член?
Розв’язання
![]()
![]()
![]()
![]()
![]() … або
… або ![]() 4; 9; 16; 25; … . Її n-й член
4; 9; 16; 25; … . Її n-й член ![]() .
.
Приклад 2. Напишіть кілька перших членів послідовності натуральних чисел, кратних 3. Обчисліть її сороковий член.
Розв’язання
3; 6; 9; 12; 15; … . Перш ніж знайти сороковий член послідовності, нам потрібно знайти її n-й член. Оскільки послідовність натуральних чисел ми позначаємо ![]() , то послідовністю натуральних чисел, кратних 3, буде
, то послідовністю натуральних чисел, кратних 3, буде ![]() . Отже
. Отже ![]()
Відповідь: 120
Приклад 3. Знайти суму всіх двоцифрових натуральних чисел, які при діленні на 3 дають остачу 2.
Розв’язання
Першим двоцифровим натуральним числом, яке при діленні на 3 дає в остачі 2, є число 11, а останнім – 98. Тому треба знайти суму членів арифметичної прогресії, в якій a1 = 11, an = 98 i d = 3.
Спочатку знайдемо число членів n. Маємо:
an = a1 + d(n – 1) = 98,
або
11 + 3(n – 1) = 98.
Звідси n = 30.
Тепер обчислимо шукану суму
![]() .
.
Відповідь: 1635.
Приклад 4. Розв’язати рівняння
![]()
за умови, що ![]() .
.
Розв’язання
Звівши до спільного знаменника, отримаємо:
![]() .
.
Легко бачити, що в чисельнику отримали суму n перших членів арифметичної прогресії, в якій ![]() ,
, ![]() ,
, ![]() .
.
Скориставшись формулою суми n перших членів арифметичної прогресії
![]() ,
,
отримуємо: ![]() .
.
Таким чином, маємо рівняння:
![]()
![]()
![]()
![]()
![]() або
або ![]() .
.
Відповідь. 3.
Приклад 5. Наталка і Сашко грають у таку гру: один з них називає число, що не перевищує 10, другий додає до нього деяке число, що також не перевищує 10, і називає суму; тоді перший додає до названої суми число не більше 10 і називає нову суму і т.д. Виграє той, хто першим назве число 100. Починає гру Наталка. Як вона повинна грати, щоб перемогти, незалежно від того, які числа називає Сашко?
Розв’язання
Наталка виграє, коли перед тим, як назвати число 100, назве число 89. Число 89 вона зможе назвати після 78 і т.д. Отже, щоб перемогти, Наталці необхідно називати числа 1, 12, 23, 34, 45, 56, 67, 78, 89, 100, які утворюють арифметичну прогресію, перший член якої 1, а різниця 11.
У загальному випадку, якщо вибрано деяке число M і двоє грають, додаючи до названого попереднім учасником гри деяке число, яке не перевищує m, то той, хто починає, завжди виграє, якщо він називає числа, що утворюють арифметичну прогресію, перший член якої – остача від ділення M на m+1, а різниця дорівнює m+1.
Приклад 6. Плавець під час першого тренування подолав дистанцію у 450 м. Кожного наступного тренування він пропливав на 50 м більше, ніж поперднього, поки не досягнув результату - 1000 м за одне тренування. Після цього під час кожного відвідування басейну плавець пропливав 1000 м. Скільки всього кілометрів плавець проплив за перші 10 тижнів тренувань, якщо він тренувався тричі кожного тижня?
Розв’язання
Легко бачити, що в умові задано арифметичну прогресію, перший член якої рівний ![]() , а різниця рівна
, а різниця рівна ![]() . Знайдемо спочатку номер тренування, під час якого спортсменом було досягнуто результат 1000м. Згідно формули загального члена арифметичної прогресії
. Знайдемо спочатку номер тренування, під час якого спортсменом було досягнуто результат 1000м. Згідно формули загального члена арифметичної прогресії
![]() ,
,
маємо:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Згідно формули суми n перших членів арифметичної прогресії
![]()
маємо:
![]() м – стільки плавець всього проплив, доки не досягнув результату 1000 м, причому цей результат було досягнуто за 12 тренувань. Всього плавець тренувався тричі кожного тижня, тоді оскільки в умові задачі питається про перші 10 тижнів тренувань, то залишається знайти, скільки плавець проплив за решту 30–12=18 тренувань. Згідно умови задачі, ці 18 тренувань плавець пропливав по 1000м, тому проплив він
м – стільки плавець всього проплив, доки не досягнув результату 1000 м, причому цей результат було досягнуто за 12 тренувань. Всього плавець тренувався тричі кожного тижня, тоді оскільки в умові задачі питається про перші 10 тижнів тренувань, то залишається знайти, скільки плавець проплив за решту 30–12=18 тренувань. Згідно умови задачі, ці 18 тренувань плавець пропливав по 1000м, тому проплив він ![]() м.
м.
Отже, всього плавець проплив
![]() м, тобто 26,7км.
м, тобто 26,7км.
Відповідь: 26,7.
Приклад 7: Знайдіть суму ![]() .
.
Розв’язання:
Маємо:![]() .
.
Тоді задану суму можна переписати так: ![]()
![]()
=![]() .
.
Отже, ![]() .
.
Приклад 8: Знайдіть суму 7+77+777+![]() .
.
Розв’язання:
Оскільки ![]() , то для розв’язання задачі достатньо знайти таку суму:
, то для розв’язання задачі достатньо знайти таку суму:
![]()
Маємо: ![]()
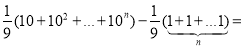
![]() .
.
Отже, шукана сума дорівнює ![]()
Відповідь:![]()
1.7. Завдання для самостійного опрацювання
1. Довести, що послідовність (an) є зростаючою :
1) an = n2 + n – 1 ; 2) an = ![]() .
.
2. Довести, що послідовність (an) є спадною :
1) an = - n2 + n + 1 ; 2) an = ![]() .
.
3. Яка з наведених послідовностей (xn) є зростаючою?
1) xn = ![]() ; 2) xn = 11 - 8n ; 3) xn=
; 2) xn = 11 - 8n ; 3) xn= ![]() ; 4) xn =
; 4) xn = ![]() .
.
4. Яка з наведених послідовностей (xn) є спадною?
1) xn = n2 +1 ; 2) xn = ![]() ; 3) xn = 7n – 12 ; 4) xn =
; 3) xn = 7n – 12 ; 4) xn = ![]() .
.
5. Знайти перший член геометричної прогресії, якщо її третій член дорівнює ![]() , а його квадрат в сумі з сьомим членом дає потроєний п’ятий член.
, а його квадрат в сумі з сьомим членом дає потроєний п’ятий член.
6.В арифметичній прогресії сума членів з четвертого по чотирнадцятий включно дорівнює ![]() . Знайти номер члена прогресії, який дорівнює
. Знайти номер члена прогресії, який дорівнює ![]() .
.
7. При яких значеннях ![]() числа
числа ![]() ,
, ![]() ,
, ![]() утворюють арифметичну прогресію
утворюють арифметичну прогресію ![]() ?
?
8. Яке найбільше число членів може містити скінченна арифметична прогресія з різницею ![]() при умові, що квадрат її першого члена в сумі з решту членами не перевищує
при умові, що квадрат її першого члена в сумі з решту членами не перевищує ![]() ?
?
9. Числа ![]() ,
,![]() ,
,![]() ,
,![]() – послідовні члени геометричної прогресії. Відомо, що
– послідовні члени геометричної прогресії. Відомо, що ![]() ,
, ![]() . Знайти
. Знайти ![]() .
.
11.Дані арифметичні і геометричні прогресії. Сума їх перших членів дорівнює ![]() , сума третіх дорівнює
, сума третіх дорівнює ![]() , сума п’ятих дорівнює
, сума п’ятих дорівнює ![]() . Знайти різницю арифметичної прогресії.
. Знайти різницю арифметичної прогресії.
12.В зростаючій геометричній прогресії сума першого і останнього членів дорівнює ![]() , а добуток другого і передостаннього членів дорівнює
, а добуток другого і передостаннього членів дорівнює ![]() . Знайти останній член прогресії.
. Знайти останній член прогресії.
13.Всі члени арифметичної прогресії – натуральні числа. ![]() ,
, ![]() Знайти прогресію.
Знайти прогресію.
14.Три відмінні від нуля дійсні числа утворюють арифметичну прогресію, а їх квадрати в тому ж порядку – геометричну. Знайти всі можливі значення ![]() .
.
15.В геометричній прогресії добуток першого та п’ятого членів дорівнює ![]() , а частка другого та четвертого членів дорівнює
, а частка другого та четвертого членів дорівнює ![]() . Знайти другий член прогресії.
. Знайти другий член прогресії.
16. В геометричній прогресії сума перших п’яти членів дорівнює п’ятьом першим членам, а сума перших п’ятнадцяти членів дорівнює ![]() . Знайти суму першого, шостого та одинадцятого членів прогресії.
. Знайти суму першого, шостого та одинадцятого членів прогресії.
17. Дві геометричні прогресії мають однакові перші члени рівні ![]() . Сума других членів дорівнює
. Сума других членів дорівнює ![]() , сума п’ятих дорівнює
, сума п’ятих дорівнює ![]() . Знайти суму шостих членів.
. Знайти суму шостих членів.
18. Знайти арифметичну прогресію, в якій скільки б не взяти членів, завжди їх сума дорівнює потроєному квадрату числа її членів.
19. Числа ![]() ,
,![]() ,
,![]() ,
,![]() утворюють геометричну прогресію. Знайти
утворюють геометричну прогресію. Знайти ![]() .
.
20.Знайти суму всіх трицифрових натуральних чисел, які при діленні на 5 дають остачу 1.
21. Два тіла, відстань між якими 153 м, рухаються назустріч один одному. Перше тіло проходить щосекунди по 10 м; друге ж за першу секунду пройшло 3 м, а кожної наступної секунди проходить на 5 м більше, ніж за попередню секунду. Через скільки секунд тіла зустрінуться?
22.Знайдіть суму 1*2+2*3+...+ n(n+1)
23.Знайдіть суму 9+99+999+...+![]()
2.Дедукція та індукція.
Різновиди індукцій та їх використання.
2.1.Поняття дедукція та індукція
Дедукція та індукція – це основні методи наукового мислення, тобто міркувань, висновків, дослідів.
У математиці, теоретичній механіці, теоретичній фізиці, математичній лінгвістиці використовується дедуктивна побудова теорії. Слово «дедукція» в перекладі на українську мову означає «виведення». Дедуктивне міркування – це міркування від загального до конкретного, тобто міркування , вихідним моментом якого є загальне міркування , а кінцевим моментом – конкретний випадок.
Але часто і в математиці, а особливо в науках, пов’язаних з експериментами, із вивченням природних явищ, спостерігається повторення будь – яких властивостей, або «конкретностей». Це повторення наводить на думку про закономірності. Загальні висновки , отримані на підставі окремих випадків , називаються індуктивними , а сам метод таких міркувань – індуктивним методом або індукцією ( від латинського inductio- наведення).
Наприклад, задовго до відкриття законів руху Землі люди зробили висновок , що Сонце вранці встає на сході, а ввечері зникає за обрієм на заході. Цей висновок є індуктивним: адже він базується лише на спостереженнях.
Звісно за допомогою індукції не завжди можна отримати правильні висновки. Так, якщо в нашій школі серед учителів початкових класів немає чоловіків , то це не означає , що всі вчителі початкових класів – жінки.
Індукція – це метод мислення – не може бути зведенням до простого перелічення обмеженого числа сприятливих випадків. Проста перелічильна індукція частіше приводить до помилкових , ніж до істинних узагальнень та в кращому випадку має евристичне значення наведення на більш або менш імовірні припущення. Наукові принципи індукції були розроблені понад 400 років тому англійським ученим Френсісом Беконом . Він уперше поставив перед собою проблему сформулювати принципи наукової індукції, яка «проводила б у досліді поділ на відбір та шляхом необхідних виключень й відкидань робила б необхідні висновки» .

![]() Індукція є основним методом досліджень в експериментальних науках. Але її роль велика і в математиці, бо вона дозволяє в пошуках нового загального закону використовувати виникаючі при цьому гіпотези, відкидати невірні та стверджувати істинні. Тема «метод математичної індукції» займає важливе місце в курсі математики, бо закладає основи аналітичного мислення, формує інтуїцію,
Індукція є основним методом досліджень в експериментальних науках. Але її роль велика і в математиці, бо вона дозволяє в пошуках нового загального закону використовувати виникаючі при цьому гіпотези, відкидати невірні та стверджувати істинні. Тема «метод математичної індукції» займає важливе місце в курсі математики, бо закладає основи аналітичного мислення, формує інтуїцію,
розвиває увагу, уміння аналізувати, висувати
Френсіс Бекон наукові гіпотези та доводити їх або спростовувати ;
за допомогою методу математичної індукції можна розв’язати великий клас задач.
2.2. Повна та неповна індукції
Найпростішим методом індуктивного міркування є повна індукція. Вона полягає в тому ,що загальне твердження доводиться поодинці, в кожному з обмеженого числа можливих випадків.
Приклад 1. Довести, що для всіх дійсних ![]() і
і ![]() справедливе твердження:
справедливе твердження:
![]()
Розв’язання.
Можливі чотири випадки:
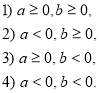
Розглянемо кожен з випадків.
1) Якщо ![]() , то
, то ![]()
![]() і нерівність набуде такого вигляду
і нерівність набуде такого вигляду ![]() та є істинним твердженням.
та є істинним твердженням.
2) Якщо ![]() то
то ![]() і тому
і тому ![]() не більший за більше з чисел
не більший за більше з чисел ![]() та
та ![]() . Але тоді
. Але тоді ![]()
3) Якщо ![]() , то доведення нерівності аналогічне випадку 2.
, то доведення нерівності аналогічне випадку 2.
4) У випадку , коли ![]() , матимемо:
, матимемо:
![]() і тому твердження
і тому твердження ![]() істинне.
істинне.
Отже, дана нерівність є істинною в кожному з чотирьох можливих випадків.
Такий метод перебору скінченої кількості всіх можливих випадків називають повною індукцією.
Приклад 2. У 1742 році член Петербурзької Академії наук Х.Гольдбах у листі до Л.Ейлера висловив гіпотезу , що кожне парне число, більше від 2,можна подати як суму двох простих чисел. Ця гіпотеза досі не доведена і не спростована . Але , якщо обмежитись числами , меншими від певного числа, то таке твердження можна довести (демонстрація портретів учених)
Доведення.
Доведемо, наприклад, що всяке парне число , яке задовольняє нерівність ![]() , можна представити у вигляді суми двох простих чисел. Оскільки таких простих чисел скінчене число, то це твердження можна довести методом повної індукції, розглянувши всі можливі випадки: 4=2+2, 6=3+3, 8=3+5, 10=3+7, 12=5+7, 14=3+11, 16=5+11, 18=5+13, 20=3+17, 22=5+17, 24=7+17, 26=13+13, 28=5+23, 30=7+23.
, можна представити у вигляді суми двох простих чисел. Оскільки таких простих чисел скінчене число, то це твердження можна довести методом повної індукції, розглянувши всі можливі випадки: 4=2+2, 6=3+3, 8=3+5, 10=3+7, 12=5+7, 14=3+11, 16=5+11, 18=5+13, 20=3+17, 22=5+17, 24=7+17, 26=13+13, 28=5+23, 30=7+23.
Тим самим сформульоване твердження доведене.
Суттєвий результат у цьому напрямі зробив російський математик, академік Іван Матвійович Виноградов, який довів, що будь – яке досить велике парне число є сумою чотирьох простих чисел.
Необхідно відмітити, що іноді індуктивні міркування приводять до невірних висновків. Розглядаючи числа виду![]() , французький математик ХVІІ століття П’єр Ферма , помітив, що всі числа такого виду прості. Однак видатний математик ХVІІІ століття Леонард Ейлер знайшов, що вже при
, французький математик ХVІІ століття П’єр Ферма , помітив, що всі числа такого виду прості. Однак видатний математик ХVІІІ століття Леонард Ейлер знайшов, що вже при ![]() число
число ![]() не є простим, воно ділиться на 641.
не є простим, воно ділиться на 641.
 Наведемо приклад , що належить члену Петербурзької академії наук Л.Ейлеру. Розглянемо квадратний тричлен
Наведемо приклад , що належить члену Петербурзької академії наук Л.Ейлеру. Розглянемо квадратний тричлен ![]() і обчислимо значення многочлена при
і обчислимо значення многочлена при ![]() дістанемо :
дістанемо :
![]() Легко помітити, що всі ці числа прості. Підставляючи
Легко помітити, що всі ці числа прості. Підставляючи

![]() , ми ще довго діставатимемо прості числа . Тому природно висловити гіпотезу,
, ми ще довго діставатимемо прості числа . Тому природно висловити гіпотезу,
Блез Паскаль
що значення ![]() при всіх натуральних
при всіх натуральних ![]() є простими. Але ця гіпотеза є неправильною, оскільки, якщо
є простими. Але ця гіпотеза є неправильною, оскільки, якщо ![]() , ми дістанемо,
, ми дістанемо, ![]() , тобто
, тобто ![]() - складене число.
- складене число.
Отже, індукція може привести як до правильних, так і неправильних висновків. Можливість неправильного Якоб Бернуллі
висновку при індукції пов’язана з тим, що ми розглядаємо лише окремі випадки і хочемо зробити на основі цього загальний висновок. Тому таку індукцію часто називають неповною. Даний метод неповної індукції можна використовувати лише для того, щоб висловити деяку правдоподібну гіпотезу, яку потім необхідно або довести або спростувати.
Для індуктивного переходу від твердження перевіреного на скінченій підмножині до аналогічного твердження для всієї нескінченої множини необхідно доведення. Але як здійснити перевірку для нескінченого числа випадків?
Такий спосіб запропонували Б.Паскаль та Я.Бернуллі. Тепер він має назву – метод математичної індукції. А базується він на принципі математичної індукції.
2.3.Принцип математичної індукції.
Метод математичної індукції
Якщо твердження , у формулюванні якого є натуральне число ![]() , істинне , коли
, істинне , коли ![]() , і зі справедливості даного твердження , коли
, і зі справедливості даного твердження , коли ![]()
![]() , випливає його справедливість , коли
, випливає його справедливість , коли ![]() , то твердження є істинним для всіх
, то твердження є істинним для всіх ![]() .
.
Цей принцип за змістом досить очевидний , приймають за одну з аксіом натуральних чисел і називають принципом математичної індукції
Метод доведення, що ґрунтується на принципові математичної індукції, називається методом математичної індукції.
Доведення методом математичної індукції проводиться так. Спочатку твердження перевіряють при ![]() . Цю частину доведення називають базою індукції. Якщо при
. Цю частину доведення називають базою індукції. Якщо при ![]() твердження істинне, то переходять до другої частини доведення , що називають індуктивним кроком або індуктивним переходом. У цій частині доводять справедливість твердження для
твердження істинне, то переходять до другої частини доведення , що називають індуктивним кроком або індуктивним переходом. У цій частині доводять справедливість твердження для ![]() , допускаючи істинність твердження , коли
, допускаючи істинність твердження , коли ![]() .
.
Опорна схема
-
Перевіряємо істинність твердження при
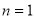
-
Припускаємо істинність твердження при
 та доводимо істинність твердження при
та доводимо істинність твердження при 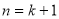 .
.
-
Робимо висновок про істинність твердження для будь-якого натурального
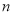 .
.
Приклад 1: Довести, що довільну суму , більшу 7 копійок , можна сплатити монетами вартістю в 3 коп. та 5 коп.
Доведення.
1)База індукції. Суму в 8 копійок , очевидно можна сплатити.
2) Індуктивний перехід. Припустимо, що нам вдалося сплатити суму в ![]() копійок вказаними монетами. Якщо серед них є монета в 5 коп., то замінимо її на дві монети по 3 коп. і одержимо суму в
копійок вказаними монетами. Якщо серед них є монета в 5 коп., то замінимо її на дві монети по 3 коп. і одержимо суму в ![]() копійку. Якщо ж всі монети суми по 3 коп., то їх не менше трьох, і замінивши три монети по 3 коп. на дві монети по 5 коп., ми також збільшимо суму на 1 копійку.
копійку. Якщо ж всі монети суми по 3 коп., то їх не менше трьох, і замінивши три монети по 3 коп. на дві монети по 5 коп., ми також збільшимо суму на 1 копійку.
Приклад 2: Обчислити суму ![]() перших непарних натуральних чисел.
перших непарних натуральних чисел.
Розв’язання.
Будемо спостерігати як «поводиться» сума ![]() перших непарних чисел. Маємо:
перших непарних чисел. Маємо:
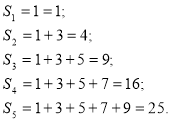
Числа 1,4,9,16,25 є квадратами послідовних натуральних чисел.
Тепер можна зробити припущення, що для будь – якого натурального ![]() :
: ![]()
Доведемо цей факт методом математичної індукції.
1). База індукції .Перевіряємо істинність твердження при ![]() .
.
![]() .
.
2) Індуктивний перехід .Припустимо, що дане твердження істинне при ![]() , тобто твердження :
, тобто твердження : ![]() - справедливе.
- справедливе.
Доведемо, що дана рівність справедлива і коли ![]() , тобто є правильною рівність:
, тобто є правильною рівність: ![]()
Розглянемо ліву частину
![]()
Але за припущенням індукції , сума ![]() .
.
Отже, вся сума дорівнює ![]()
За принципом математичної індукції , істинність твердження доведено для будь – якого ![]() .
.
2.4. Вивчення властивостей числових послідовностей
Арифметична та геометрична послідовності визначаються рекурентними співвідношеннями ![]() та
та ![]() відповідно. За допомогою методу математичної індукції можна довести ці формули, а також формули для знаходження суми
відповідно. За допомогою методу математичної індукції можна довести ці формули, а також формули для знаходження суми ![]() перших членів цих відомих послідовностей.
перших членів цих відомих послідовностей.
Приклад 1. Довести формулу ![]() -го члена арифметичної прогресії
-го члена арифметичної прогресії ![]()
Доведення.
1). База індукції. Якщо ![]() ,то формула набуває вигляду :
,то формула набуває вигляду :![]()
2). Індуктивний перехід. Припустимо, що коли ![]() , правильною є формула
, правильною є формула ![]() , і доведемо істинність при
, і доведемо істинність при ![]() , тобто
, тобто ![]() .
.
![]()
За принципом математичної індукції формула для ![]() -го члена арифметичної прогресії є правильною для будь – яких натуральних значень
-го члена арифметичної прогресії є правильною для будь – яких натуральних значень ![]() .
.
Приклад 2. Довести , що суму ![]() перших членів геометричної прогресії можна обчислити за формулою
перших членів геометричної прогресії можна обчислити за формулою
![]() де
де ![]() - перший член послідовності,
- перший член послідовності, ![]() - знаменник геометричної прогресії
- знаменник геометричної прогресії
Розв’язання.
Розглянемо два випадки.
1. Якщо ![]() , то
, то ![]() , тобто формула є правильною.
, тобто формула є правильною.
2. Якщо ![]() , то скористаємось методом математичної індукції.
, то скористаємось методом математичної індукції.
1) База індукції. Якщо ![]() , то формула набуває вигляду
, то формула набуває вигляду ![]() і є істинною.
і є істинною.
2) Індуктивний перехід. Припустимо, що коли ![]() , правильною є формула
, правильною є формула ![]() і доведемо, що коли
і доведемо, що коли ![]() , має місце співвідношення
, має місце співвідношення ![]()
Враховуючи, що ![]() та припущення індукції матимемо :
та припущення індукції матимемо :
![]()
За принципом математичної індукції формула для знаходження суми ![]() перших членів геометричної прогресії є правильною для будь – яких натуральних значень
перших членів геометричної прогресії є правильною для будь – яких натуральних значень ![]() .
.
Приклад 3. Послідовність ![]() задана рекурентно :
задана рекурентно : ![]() .Довести, що цю послідовність можна задати формулою
.Довести, що цю послідовність можна задати формулою ![]() го члена
го члена ![]()
Доведення.
Доведення проведемо методом математичної індукції.
Якщо ![]() , то твердження правильне, бо
, то твердження правильне, бо ![]() .
.
Якщо ![]() , то твердження правильне, бо
, то твердження правильне, бо ![]()
Нехай ![]() і
і ![]() Маємо:
Маємо:
![]() Тим самим формула істинна для будь - якого натурального
Тим самим формула істинна для будь - якого натурального ![]() .
.
2.5.Завдання для самостійного опрацювання
- Нехай послідовність аn-арифметична прогресія з різницею d. Доведіть методом математичної індукції формули для загального члена і для суми n членів:
a n =a1+(n-1) d; ![]()
- Нехай послідовність bn- геометрична прогресія із знаменником q. Доведіть методом математичної індукції формули для загального члена і для суми n членів:
bn= b1qn-1; ![]()
- Доведіть, що для всіх натуральних n виконується рівність:
а)1+2+3+...+ n=![]() ;
;
б)12+22+32+…n2=![]() .
.
3.Рекурентні послідовності.
Перехід від рекурентно заданої послідовності до аналітично заданої.
3.1.Рекурентний спосіб послідовності
Числова послідовність – особливий клас функцій, тому, крім раніше вивчених способів задання функцій, а саме: словесний, графічний, табличний, аналітичний тощо. Є спосіб характерний для числових послідовностей – рекурентний („від попереднього”) або індуктивний. Слід пам’ятати, що опис тільки перших її членів приховує в собі можливість помилки, при подальшому запису членів послідовності.
Розглянемо приклад числової послідовності:
1,1,2,3,5,8,13,21,... В цьому випадку за допомогою кількох членів не можна однозначно продовжити послідовність. Ця послідовність називається на честь італійського математика ХІІІ століття Фібоначчі. Спосіб задання – рекурентний.
При рекурентному способі задання послідовності задають:
а) перший член послідовності, або кілька перших членів;
б) формулу, яка дає можливість визначити будь-який член послідовності за відомими попередніми членами.
 a1=1, a2=1, an=an-2+an-1, коли n ≥ 3.
a1=1, a2=1, an=an-2+an-1, коли n ≥ 3.
Перехід від рекурентного задання послідовності до аналітичного може бути важким. Лише французький математик Біне Жак Філіп Марі (1786-1856) аналітично задав послідовність Фібоначчі
Біне Жак Філіп Марі Наприклад, для послідовності простих чисел 2,3,5,7,11,13,17,19,... формула будь-якого члена (записана явно як функція від n) ще невідома!
Приклад 1. Числова послідовність задана рекурентною формулою аn+2=an2-an+1; a1=2, a2=3. Обчислити п'ятий член послідовності.
Розв'язання:
a1=2, a2=3; за формулою а1+2=а12- а1+1; а3 =22-3; а3=1;
Знаючи а3 = 1; а2+2=а22-а2+1; а4=а22 -а3; а4=32-1; а4=8;
а5=а32-а4; а5=12-8=-7
Відповідь: -7.
Приклад 2. Послідовність аn задана формулою n-го члена ![]() . Задайте її рекурентно.
. Задайте її рекурентно.
Розв’язання:
Маємо а1=2. У формулі n-го члена виразимо n через аn. Маємо: nаn =n+1 n( аn.- 1)=1. Оскільки аn. ![]() 1 при будь-якому n
1 при будь-якому n![]() N , то можна записати
N , то можна записати ![]() .
.
Маємо: 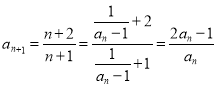 .
.
Відповідь: а1=2, ![]()
Приклад 3: Послідовність аn. Задана рекурентно: а1 =5, а2=13, ![]() . Доведіть, щоцю послідовність можна задати формулою n-го члена
. Доведіть, щоцю послідовність можна задати формулою n-го члена ![]() .
.
Розв’язання:
Доведення проведемо методом математичної індукції.
При n=1 ![]() , при
, при ![]() ,
, ![]() , тобто теорема “база індукції” є правильною.
, тобто теорема “база індукції” є правильною.
Нехай ![]() і
і ![]() . Маємо:
. Маємо:![]() Тим самим доведено теорему “індуктивний перехід”
Тим самим доведено теорему “індуктивний перехід”
Отже, ![]() для будь-якого n.
для будь-якого n.
Приклад 4: Послідовність аn задана рекурентно: а1=1, а2=2, ![]() . Знайдіть а2010.
. Знайдіть а2010.
Розв’язання:
Запишемо кілька перших членів послідовності:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
У даній послідовності кожний член, починаючи з третього, однозначно визначається двома попередніми членами.Бачимо, що .![]()
![]() . Отже, не проводячи подальших обчислень, можна зробити висновок, що
. Отже, не проводячи подальших обчислень, можна зробити висновок, що ![]()
![]()
![]() і взагалі
і взагалі ![]() для будь-якого натурального n. Така послідовність є періодичною з періодом 5. У цій послідовності члени, номери яких конгруентні за модулем 5 рівні. Звідси, а2010=а5=1
для будь-якого натурального n. Така послідовність є періодичною з періодом 5. У цій послідовності члени, номери яких конгруентні за модулем 5 рівні. Звідси, а2010=а5=1
 3.2.Числа Фібоначчі
3.2.Числа Фібоначчі
На початку ХІІІ століття в місті Піза (Італія) жив великий знавець всеможливих співвідношень між числами і вельми вправний рахівник Леонардо (до його імені додавали Пізанський). Звали його Фібоначчі, що означало син Боначчі. В 1202 році він видав книгу на латинській мові "Книга про абаке" – одна із перших книг в Європі , де вживалась десяткова система числення. За традиціями того часу Леонардо Пізанський
Фібоначчі був учасником публічних математичних турнірів (сучасні олімпіади).
Його майстерність вважала всіх. Так у 1225 році государ Римської імперії Фрідріх ІІ, що приїхав на турнір у супроводі математиків запропонував задачу: знайти повний квадрат, який залишається повним квадратом як після збільшення, так і після зменшення його на 5. Фібоначчі після деяких розмірковувань знайшов це число.
Воно виявилось дробовим: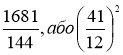 . Якими міркуваннями керувався Фібоначчі під час турніру, ми не з'ясовуємо, але розв'язав блискуче.
. Якими міркуваннями керувався Фібоначчі під час турніру, ми не з'ясовуємо, але розв'язав блискуче.

Відео “Число Бога”
Властивості чисел Фібоначчі
- Квадрат кожного члену ряду Фібоначчі, зменшений на добуток попереднього і наступного членів, дає по черзі +1, та -1.
Наприклад:
22-1·3=+1
32-2·5=-1
52-3·8=+1
...
Sn2-Sn+1·Sn+1=(-1)n+1;
2) Будь яка пара сусідніх чисел ряду Фібоначчі задовольняє умову одно із рівнянь x2-xy-y2=±1; при цьому більше значення - х, менше - у. Наприклад 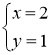 або
або 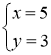 або
або  тощо є корені першого рівняння
тощо є корені першого рівняння
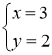
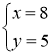
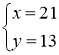 тощо корені другого рівняння.
тощо корені другого рівняння.
 Листя на гілці розміщені одинаково, по гвинтовій лінії, тобто наступний лист вище в сторону від попереднього. Для кожної рослини характерний свій путь розходження листочків. Цей кут – дріб, що вказує яку частину кола він складає. У липи і вяза
Листя на гілці розміщені одинаково, по гвинтовій лінії, тобто наступний лист вище в сторону від попереднього. Для кожної рослини характерний свій путь розходження листочків. Цей кут – дріб, що вказує яку частину кола він складає. У липи і вяза ![]() кола, у бука –
кола, у бука – ![]() , у дуба і вишні
, у дуба і вишні ![]() , у тополі і груші
, у тополі і груші ![]() , у верби
, у верби ![]() тощо. Ряд чисельників і ряд знаменників – числа Фібоначчі.
тощо. Ряд чисельників і ряд знаменників – числа Фібоначчі.
3) S1+S3+...+S2n-1=S2n;
4) S2+S4+...+S2n=S2n+1 -1
5) У ряді Фібоначчі кожне третє число – парне, кожне четверте ділиться на 3, кожне п'яте на 5, кожне п'ятнадцяте на 10.
6) Неможливо побудувати трикутник, сторонами якого є числа Фібоначчі
7) Якщо взяти будь-які 4 послідовних числа ряду Фібоначчі і розглядати добуток крайніх членів і подвоєний добуток середніх як довжин катетів прямокутного трикутника, то довжина його гіпотенузи буде один з членів цього ряду ![]()
8) Сума квадратів чисел ряду Фібоначчі виражається через добуток двох сусідніх членів ряду
S12+S22+...+Sn2=Sn · Sn+1;
-
Знаючи, а1=
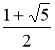 і а2=
і а2=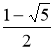 , будь-який член Sn ряду визначається за номером Sn=
, будь-який член Sn ряду визначається за номером Sn=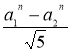
3.2.Завдання для самостійного опрацювання
-
Послідовність
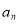 задана рекурентно:
задана рекурентно: 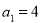
 . Знайдіть
. Знайдіть 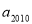 .
.
- Послідовність задана формулою n -го члена. Задайте її рекурентно:
-
 ;
;
-
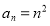 ;
;
-
 .
.
- Знайдіть формулу n-го члена послідовності , заданої рекурентно:
-
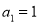 ,
, 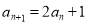 ;
;
-
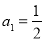 ,
, 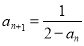 .
.
-
Послідовність
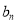 задана рекурентно:
задана рекурентно: 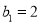 ,
, 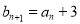 . Чи є членом цієї послідовності число 1024?
. Чи є членом цієї послідовності число 1024?
-
Послідовність
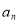 задана рекурентно:
задана рекурентно: 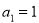 ,
, 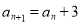 . Чи є членом цієї послідовності число 2010?
. Чи є членом цієї послідовності число 2010?
- Границя числової послідовності.
4.1. Уявлення про границю послідовності.
Означення. Число а називається границею послідовності ![]() , якщо для будь-якого
, якщо для будь-якого ![]() , яке б мале воно не було, існує номер N такий, що для всіх номерів
, яке б мале воно не було, існує номер N такий, що для всіх номерів ![]() виконується нерівність
виконується нерівність ![]() .
.
Позначення: ![]() або
або ![]() .
.
( lim- це початкові літери французького слова limite-границя)
Для стислого запису означення границі використаємо квантори: — для будь-якого, будь-який; — існує, знайдеться; : = дорівнює за означенням, означає. Тоді означення границі послідовності за допомогою цих символів запишеться так:
![]()
Розглянемо геометричну інтерпретацію границі послідовності. На числовій осі побудуємо -окіл числа а, тобто інтервал (а – ; а + ), і покажемо, як розміщуватимуться точки, які відповідають членам послідовності ![]() , при
, при ![]()
![]()
Рис. 1
Означення. Число а називається границею послідовності xn, якщо для будь-якого -околу точки а існує номер N такий, що, починаючи з номерів ![]() , усі члени послідовності перебувають в -околі точки а (див. рис. 1).
, усі члени послідовності перебувають в -околі точки а (див. рис. 1).
Наприклад: Розглянемо послідовність вn задану формулою n-го члена ![]() . Випишемо кілька перших членів цієї послідовності:
. Випишемо кілька перших членів цієї послідовності:
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,...
,...
Зі збільшенням номера члени послідовності прямують до числа 2. Це означає, що для будь-якого члена ![]() можна вказати такий номер
можна вказати такий номер ![]() , що для всіх
, що для всіх![]() виконується нерівність
виконується нерівність ![]() . Оскільки
. Оскільки 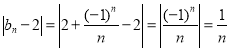 , то номер n можна знайти, розв’язавши нерівність
, то номер n можна знайти, розв’язавши нерівність![]() .
.
Отже, ![]()
Означення. Послідовність називається збіжною, якщо вона має границю (скінченну). Послідовність, яка не має границі, називається розбіжною.
Наприклад: Послідовність з n-м членом ![]() є збіжною послідовністю: зі збільшенням номера n-члени послідовності прямують до 0, тобто
є збіжною послідовністю: зі збільшенням номера n-члени послідовності прямують до 0, тобто ![]() . Послідовність натуральних чисел не є збіжною.
. Послідовність натуральних чисел не є збіжною. ![]() - також не є збіжною послідовністю.
- також не є збіжною послідовністю.
Приклад 1: Доведіть, що ![]()
Розв’язання:
Нехай ![]() -довільне додатне число. Знайдемо номер
-довільне додатне число. Знайдемо номер![]() такий, що для всіх
такий, що для всіх ![]() виконується нерівність
виконується нерівність![]()
![]()
Маємо: ![]() .
.
З’ясуємо, при яких ![]() виконується нерівність
виконується нерівність![]()
Переходимо до рівносильних нерівностей:![]()
![]() ;
;
![]() ;
;
![]() .
.
В якості номера ![]() візьмемо, наприклад, число
візьмемо, наприклад, число ![]() +1 Тоді, якщо
+1 Тоді, якщо ![]() , то
, то ![]() , і, переходячи до рівносильної нерівності
, і, переходячи до рівносильної нерівності![]() , а потім
, а потім ![]() , отримаємо врешті, що
, отримаємо врешті, що ![]() і
і ![]() . Тому
. Тому ![]() .
.
4.2. Нескінченно спадна геометрична прогресія
Нескінченна геометрична прогресія, в якій ![]() , називається нескінченно спадною геометричною прогресією.
, називається нескінченно спадною геометричною прогресією.
Сумою нескінченно спадної геометричної прогресії називають границю суми ![]() перших її членів при
перших її членів при ![]() :
:
.![]()
Теорема . Сума нескінченно спадної геометричної прогресії дорівнює ![]() , тобто:
, тобто:
![]()
Доведення:
![]() .
.
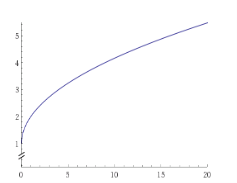
Приклад 1. Побудуйте графік функції
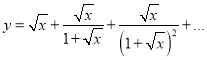 , де
, де ![]() .
.
Розв’язання
Легко бачити, що вираз у правій частині рівності є сумою нескінченно спадної геометричної прогресії з першим членом ![]() та знаменником
та знаменником ![]() .
.
Скориставшись формулою суми членів нескінченно спадної геометричної прогресії: ![]() ,
,
отримаємо:
 ,
,
тобто одержали функцію
![]() ,
,
графік якої отримується з графіка функції ![]() підняттям на одну одиницю вгору по осі Oy:
підняттям на одну одиницю вгору по осі Oy:
4.3.Завдання для самостійного опрацювання
-
Укажіть, яке число є границею послідовності
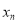 :
:
а)![]() ;
;
б)![]() ;
;
в)![]() .
.
- Доведіть, що:
а)![]() ;
;
б)![]() ;
;
в)![]() .
.
- У рівносторонній трикутник зі стороною a вписано новий трикутник, вершинами якого є сторони даного трикутника, у цей трикутник таким самим способом вписано новий трикутник і т.д. до нескінченності. Знайти суму всіх периметрів і суму усіх площ цих трикутників.
-
Побудуйте графік функції:
- У квадрат зі стороною а вписано коло, у коло вписано квадрат, у цей квадрат вписано коло, у яке знову вписано квадрат, і т.д. Знайдіть суму: 1)периметрів усіх квадратів; 2) площ квадратів; 3) довжин кіл; 4) площ кругів, обмежених даними колами.
5 .Числовий ряд, необхідна й достатня умови його збіжності, підсумування числових рядів.
5.1. Основні поняття. Деякі властивості збіжних рядів
Означення. Нехай ![]() — деяка нескінченна послідовність чисел. Побудований із цих чисел за допомогою знака «+» символ
— деяка нескінченна послідовність чисел. Побудований із цих чисел за допомогою знака «+» символ
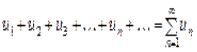 (1)
(1)
називається нескінченним рядом (чи просто рядом), а самі числа ![]() — членами ряду; n-ий член un — називається загальним членом ряду.
— членами ряду; n-ий член un — називається загальним членом ряду.
Побудуємо частинні суми ряду:
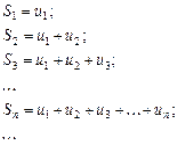 (2)
(2)
Частинні суми ряду утворюють числову послідовність: ![]()
Приклад ряду: Парадокс про Ахіллеса і черепаху
Розгляньмо сучасний варіант парадоксу, запропонованого, давньогрецьким філософом Зеноном: «Прудкий Ахіллес ніколи не наздожене черепаху, якщо перед початком руху черепаха буде попереду на деякій віддалі від нього». Припустімо, що Ахіллес бігає у десять разів швидше за черепаху, і перебуває на віддалі в 1000 метрів від черепахи. За той час, за який Ахіллес пробіжить ці 1000 метрів, черепаха проповзе 100 метрів. Коли Ахіллес пробіжить 100 метрів, черепаха проповзе ще 10 метрів тощо. Процес триватиме до нескінченності. Ахіллес так ніколи не наздожене черепаху?
Означення. Числовий ряд називається збіжним, якщо існує границя послідовності частинних сум ряду
![]() (3)
(3)
При цьому величина ![]() називається сумою ряду, а число
називається сумою ряду, а число
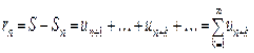 — (4)
— (4)
залишком ряду.
Означення: ряд називається розбіжним, якщо границя його часткових сум або нескінченна, або не існує. З означення випливає, що збіжність ряду зводиться до збіжності послідовності його часткових сум.
Наприклад:. Нехай ряд задано першими трьома членами ![]()
![]() . Знайти загальний член ряду і дослідити ряд на збіжність.
. Знайти загальний член ряду і дослідити ряд на збіжність.
Загальний член ряду, як правило, знаходять методом перебирання варіантів, виходячи із аналізу заданих перших членів ряду з наступною перевіркою його правильності.
У даному прикладі чисельник кожного члена дорівнює одиниці, а знаменник є добутком трьох послідовних натуральних чисел. Вважатимемо, що ![]() . Тоді, беручи n послідовно таким, що дорівнює 1, 2, 3, ..., дістаємо члени ряду
. Тоді, беручи n послідовно таким, що дорівнює 1, 2, 3, ..., дістаємо члени ряду ![]() ;
; ![]() , чим упевнюємося, що загальний член ряду
, чим упевнюємося, що загальний член ряду ![]() побудований правильно.
побудований правильно.
За допомогою методу невизначених коефіцієнтів un можна розкласти на такі дроби:
![]() .
.
Часткова сума ряду Sn запишеться тоді так:
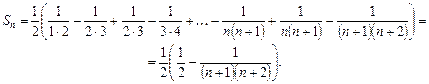
![]() . Отже, ряд збігається, його сума
. Отже, ряд збігається, його сума ![]() .
.
У цьому прикладі збіжність ряду було встановлено безпосередньо за означенням, тобто обчислено ![]() .
.


Властивості збіжних числових рядів
- Відкидання чи заміна скінченого числа членів ряду не впливає на його збіжність (розбіжність)
- Якщо члени ряду помножити на деяку константу С , його збіжність не порушиться, сума множиться на С.
-
Два збіжних ряди
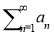 та
та 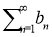 з сумами S1 та S2 можна почленно додавати або віднімати. Ряд
з сумами S1 та S2 можна почленно додавати або віднімати. Ряд 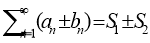
- Якщо ряд збіжний, то його члени можна групувати за порядком їх послідовності. Отриманий ряд збігається і його сума дорівнює сумі вихідного ряду.
5.2.Необхідна умова збіжності ряду
Теорема: Якщо знакододатній ряд збігається, то послідовність його членів прямує до нуля, тобто ![]()
Наслідок:(достатня умова розбіжності ряду). Якщо ![]() , то ряд
, то ряд ![]() розбігається
розбігається
Умова ![]() є лише необхідною для збіжності ряду, але не є достатньою
є лише необхідною для збіжності ряду, але не є достатньою
![]() , але ряд
, але ряд ![]() -розбігається
-розбігається
Приклад 1 : а+aq+aq2+…+aqn+…
Розв’зання:
Ряд збігається при ![]() ,
, 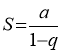
![]()
Приклад 2: Дослідити ряд на збіжність ![]()
Розв’язання:
![]() ;
; ![]()
Необхідна умова не виконується , отже ряд розбіжний
5.3.Завдання для самостійного опрацювання
1.Дослідити на збіжність ряд ![]()
2. Дослідіть на збіжність ряди:
а)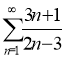 ;
;
б)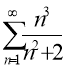 ;
;
в)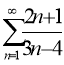 ;
;
г)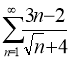


про публікацію авторської розробки
Додати розробку