Контрольна робота "Перпендикулярність прямих і площин у просторі"

Контрольна робота №3

Перпендикулярність прямих у просторі. Перпендикулярність прямої та площини

Варіант 1

У завданнях 1-2 виберіть одну правильну відповідь

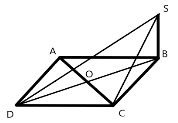1. (1 бал) До площини квадрата АВСD проведено перпендикуляр SB. Укажіть пряму, яка перпендикулярна до прямої SD

       А) BD         Б) AC        В) SA       Г) AD         Д)  AB    

2. (1 бал) Похила ВС, проведена до площини α, утворює з перпендикуляром до цієї площини кут 60°. Знайдіть проекцію похилої ВС на площину α, якщо довжина похилої дорівнює а.

А)                  Б)                В)                Г)                  Д)     

3.  (2 бали) Установити відповідність між відрізками (1-4) , побудованими на гранях і ребрах куба, та величинами кутів між ними (А-Д)

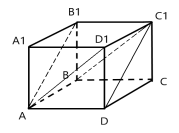
У завданнях 4-5 розв’яжіть задачу та запишіть відповідь.

4. (1 бал) Знайдіть кут між похилою АВ та площиною α, якщо довжина АВ дорівнює 30см, а точка А віддалена від площини α на 15см.

5. (2 бали) Відрізок АВ не перетинає площину α. Знайдіть відстань від середини даного відрізка до площини α, якщо його кінці віддалені від неї на 14см і 18см.

Розв’язування задач 6-7 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення.

6. (2 бали) З точки А до площини α проведено перпендикулярні похилі АВ і АС. Знайдіть відстань між точками В і С, якщо відстань від точки А до площини α дорівнює 3см, а похилі АВ і АС утворюють з площиною α кути по 60°.

7. (3 бали) У рівнобедреному трикутнику АВС АВ=ВС=17см, АС=16см. Точка Р знаходиться на відстані 8 см від усіх сторін трикутника АВС. Знайдіть відстань від точки Р до площини трикутника.

Контрольна робота №3

Перпендикулярність прямих у просторі. Перпендикулярність прямої та площини

Варіант 2

У завданнях 1-2 виберіть одну правильну відповідь

1. (1 бал) До площини квадрата АВСD проведено перпендикуляр SB. Укажіть пряму, яка перпендикулярна до прямої SС

       А) BD         Б) AC        В) SA       Г) AD         Д)  AB    

2. (1 бал) Похила ВС, проведена до площини α, утворює з перпендикуляром до цієї площини кут 60°. Знайдіть довжину похилої ВС, якщо її проекція на площину  α дорівнює а.

А)                  Б)                В)                Г)                  Д)     

3.  (2 бали) Установити відповідність між відрізками (1-4) , побудованими на гранях і ребрах куба, та величинами кутів між ними (А-Д)

У завданнях 4-5 розв’яжіть задачу та запишіть відповідь.

4. (1 бал) Знайдіть кут між похилою АВ та площиною α, якщо довжина АВ дорівнює 36см, а її проекція на площину α – 18 см.

5. (2 бали) Відрізок АВ не перетинає площину α. Знайдіть відстань від середини даного відрізка до площини α, якщо його кінці віддалені від неї на 8см і 24см.

Розв’язування задач 6-7 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення.

6. (2 бали) З точки А до площини α проведено перпендикулярні похилі АВ і АС. Знайдіть відстань від точки А до площини α, якщо довжина відрізка ВС дорівнює 10см, а похилі АВ і АС утворюють із площиною α кути по 30°.

7. (3 бали) Точка М віддалена від кожної із сторін трикутника АВС на 10см, а від його площини – на 6см. Знайдіть периметр трикутника АВС, якщо його площа дорівнює 96см².

Контрольна робота №3

Перпендикулярність прямих у просторі. Перпендикулярність прямої та площини Варіант 3

У завданнях 1-2 виберіть одну правильну відповідь

1. (1 бал) До площини квадрата АВСD проведено перпендикуляр SC. Укажіть пряму, яка перпендикулярна до прямої SD

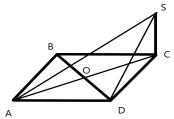       А) BD         Б) AC        В) SA       Г) AD         Д)  AB    

2. (1 бал) Похила ВС, проведена до площини α, утворює з перпендикуляром до цієї площини кут 30°. Знайдіть проекцію похилої ВС на площину α, якщо довжина похилої дорівнює а.

А)                  Б)                В)                Г)                  Д)     

3.  (2 бали) Установити відповідність між відрізками (1-4) , побудованими на гранях і ребрах куба, та величинами кутів між ними (А-Д)

У завданнях 4-5 розв’яжіть задачу та запишіть відповідь.

4. (1 бал) Знайдіть кут між похилою АВ та площиною α, якщо довжина АВ дорівнює 18см, а точка А віддалена від площини α на 9см.

5. (2 бали) Відрізок АВ не перетинає площину α. Знайдіть відстань від середини даного відрізка до площини α, якщо його кінці віддалені від неї на 11см і 19см.

Розв’язування задач 6-7 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення.

6. (2 бали) З точки А до площини α проведено перпендикулярні похилі АВ і АС. Знайдіть відстань між точками В і С, якщо відстань від точки А до площини α дорівнює 4см, а похилі АВ і АС утворюють з площиною α кути по 45°.

7. (3 бали) Точка К віддалена на 5см від кожної із сторін трикутника АВС. Знайдіть відстань від точки К до площини трикутника, якщо АВ=13см, ВС=14см, АС=15см.

Контрольна робота №3

Перпендикулярність прямих у просторі. Перпендикулярність прямої та площини Варіант 4

У завданнях 1-2 виберіть одну правильну відповідь

1. (1 бал) До площини квадрата АВСD проведено перпендикуляр SC. Укажіть пряму, яка перпендикулярна до прямої SА

       А) BD         Б) AC        В) SA       Г) AD         Д)  AB    

2. (1 бал) Похила ВС, проведена до площини α, утворює з перпендикуляром до цієї площини кут 30°. Знайдіть довжину похилої ВС, якщо її проекція на площину α дорівнює а.

А)                  Б)                В)                Г)                  Д)     

3.  (2 бали) Установити відповідність між відрізками (1-4) , побудованими на гранях і ребрах куба, та величинами кутів між ними (А-Д)

У завданнях 4-5 розв’яжіть задачу та запишіть відповідь.

4. (1 бал) Знайдіть кут між похилою АВ та площиною α, якщо довжина АВ дорівнює 32см, а її проекція на площину α – 16 см.

5. (2 бали) Відрізок АВ не перетинає площину α. Знайдіть відстань від середини даного відрізка до площини α, якщо його кінці віддалені від неї на 15см і 27см.

Розв’язування задач 6-7 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення.

6. (2 бали) З точки А до площини α проведено перпендикулярні похилі АВ і АС. Знайдіть відстань від точки А до площини α, якщо довжина відрізка ВС дорівнює 10см, а похилі АВ і АС утворюють із площиною α кути по 45°.

7. (3 бали) Точка М віддалена від кожної із сторін трикутника АВС на 13см, а від його площини – на 5см. Знайдіть периметр трикутника АВС, якщо його площа дорівнює 96см².