Річна контрольна робота з геометрії 10 клас
Річна контрольна робота з геометрії для 10 класу містить два варіанта. Завдання річної контрольної роботи складено на основі вивчених тем з геометрії відповідно до нової програми.
Річна контрольна робота 10 клас І варіант
1.(0.5 б)Дано площину 
та прямокутник АВСD. Серед даних тверджень укажіть неправильне:
А площині 
може належати тільки одна вершина прямокутника;
Б площині можуть належати дві вершини прямокутника;
В площині можуть належати лише три вершина прямокутника;
Г площині може не належати жодна з вершин прямокутника.
2. (0.5 б) Яка з точок є серединою відрізка АВ , якщо А(6;-2;8), В(-2;6;-2)?
|
А |
Б |
В |
Г |
Д |
|
(8;-8;10) |
(1;-1;0) |
(4;4;6) |
(2;2;3) |
(2;0;1) |
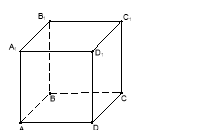3.(1б) Користуючись зображенням куба АВСDА1В1С1D1 укажіть градусну міру кута між площиною АВС1і площиною АВВ1
|
А |
Б |
В |
Г |
Д |
|
0 |
30 |
|
60 |
90 |
4. (0.5 б) Знайдіть координати вектора 
, якщо А(1;-3;5), В(5;-1;3).
|
А |
Б |
В |
Г |
Д |
|
(-4;-2;2) |
(-4;-4;-2) |
(4;2;-2) |
(6;-4;8) |
(-5;2;1) |
5.(1 б) По одну сторону від площини дано дві точки А і В на відстані 4 см і 24 см від неї.
Знайти відстань від середини відрізка АВ до даної площини.
|
А |
Б |
В |
Г |
Д |
|
7 см |
12 см |
14 см |
10 см |
4.5 см |
6 .(0.5 б) Яка з наведених точок належить площині Оуz?
|
А |
Б |
В |
Г |
Д |
|
М(0;6;2) |
К(9;З;-9) |
Р(3;0;0) |
С(5;0;9) |
В(4;-5;0) |
7.(3 б) Користуючись зображенням куба АВСDА1В1С1D1 установіть відповідність між заданими кутами (1-4) та їхніми градусними мірами (А-Д)
|
1 Кут між прямими АА1 і DС1 |
А 0 |
|
2 Кут між прямими ВD і DС1 |
Б 30 |
|
3 Кут між прямими АВ1 і А1D |
В |
|
4 Кут між прямими ВВ1 і D1D |
Г 60 |
|
|
Д 90 |
8. (1.5 б) Із точки, віддаленої від площини на 6 см, проведено дві похили під кутом 45
до площини. Знайдіть відстань між основами похилих, якщо кут між їх проекціями дорівнює 120
.
9. (1.5 б) Знайдіть кут між векторами 
і 
, якщо (0;1;-1), (-1;1;0).
10 .(2б) Побудуйте зображення правильної трикутної призми, у якої бічне ребро має довжину 3 см, а ребро основи – 4 см. Знайдіть периметр і площу перерізу, що проходить через сторону нижньої основи і протилежну вершину верхньої основи.
Річна контрольна робота 10 клас ІІ варіант
1.(0.5 б)Дано площину та коло. Серед даних тверджень укажіть неправильне:
А площині може належати тільки одна точка кола;
Б площині можуть належати дві точки кола;
В площині можуть належати лише три точки кола;
Г площині може не належати жодна з точок кола.
2.(0.5 б) Яка з точок є серединою відрізка АВ , якщо А(1;-1;1), В(1;-1;1)?
|
А |
Б |
В |
Г |
Д |
|
(2;-2;0) |
(1;-1;1) |
(-1;1;1) |
(0;1;-1) |
(2;0;1) |
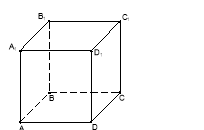3.(1 б) Користуючись зображенням куба АВСDА1В1С1D1 укажіть градусну міру кута між площиною АВС1і площиноюDСС1.
|
А |
Б |
В |
Г |
Д |
|
0 |
30 |
|
60 |
90 |
4.(0.5 б)Знайдіть координати вектора , якщо А(3,-5;0), В(-2;7;1).
|
А |
Б |
В |
Г |
Д |
|
(1;-12;-1) |
(-5;12;1) |
(-5;-12;-1) |
(1;2;1) |
(-5;2;1) |
5.(1 б) По одну сторону від площини дано дві точки А і В на відстані 6 см і 14 см від неї.
Знайти відстань від середини відрізка АВ до даної площини.
|
А |
Б |
В |
Г |
Д |
|
7 см |
10 см |
4 см |
10.5 см |
5.5 см |
6. (0.5 б) Яка з наведених точок належить площині Оху?
|
А |
Б |
В |
Г |
Д |
|
М(-1;6;2) |
К(0;З;-9) |
Р(0;0;-2) |
С(5;0;9) |
В(4;-5;0) |
7.(3 б) Користуючись зображенням куба АВСDА1В1С1D1
установіть відповідність між заданими кутами (1-4) та їхніми градусними мірами (А-Д)
|
1 Кут між прямими АВ і СС1 |
А 0 |
|
2 Кут між прямими ВD і D1С1 |
Б 30 |
|
3 Кут між прямими АD1 і В1D1 |
В |
|
4 Кут між прямими ВВ1 і АА1 |
Г 60 |
|
|
Д 90 |
8. (1.5 б) Із деякої точки до площини проведено дві похили, довжина кожної дорівнює 4 см. Вони утворюють з площиною кути по 60
Знайдіть відстань між основами похилих, якщо кут між їх проекціями дорівнює 120 .
9.(1.5 б) Знайдіть кут між векторами і , якщо (-2;-2;2), (2;2;1).
10. (2б)Побудуйте зображення правильної трикутної призми, у якої бічне ребро має довжину 5 см, а ребро основи – 12 см. Знайдіть периметр і площу перерізу, що проходить через сторону нижньої основи і протилежну вершину верхньої основи.
-
Варіант 1 завдання 7 (на відповідність ) №2 і №3 мають однакову відповідь: 60.
про публікацію авторської розробки
Додати розробку