Контрольна робота з геометрії у 10 класі - «Вступ до стереометрії»
Контрольна робота 2 «Вступ до стереометрії» 10 кл. (профільний рівень)
Мета: перевірка навчальних досягнень учнів з теми «Вступ до стереометрії»
Контрольна робота №1 «Вступ до стереометрії» 10кл.
Варіант – 1
1.Установіть відповідність між геометричними фігурами ( 1 – 4) та кількістю площин (А – Д), які вони визначають.
|
1. пряма і точка, яка лежить на прямій 2. три точки, які не лежать на одній прямій 3. дві точки кола і його центр 4. чотири точки
|
А) жодної площини Б) тільки одна площина В) жодної або одна площина Г) безліч або одна площина Д) безліч площин
|
|
2. На площині 
позначити точки А і В, а точку М – поза площиною 
. Установіть відповідність між умовою (1 – 4) та відповіддю (А – Д).
|
1. як розміщена пряма АВ відносно площини
2. як розміщена пряма ВМ відносно площини 3. якій площині належать пряма АМ і точка В? 4. скільки площин проходить через точки А, В, М? |
А)перетинає площину Б) АВМ В)належить площині Г) тільки одна Д) безліч площин
|
|
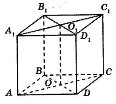3. Дано зображення куба АВСDА1В1С1D1. Установіть відповідність між площинами (1 – 4) та прямими їхнього перетину (А – Д).
|
1. АВВ1 і АDD1 2. АА1С1 і АВС 3. АА1С1 і ВВ1D1 4. А1С1D і АА1D1
|
А) ОО1 Б) АА1 В) А1D Г) DD1 Д) АС |
|
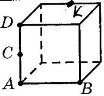4. Скільки граней куба проходить через указані точки? Установіть відповідність між умовою (1 – 4) та відповіддю (А – Д).
|
1. точку D 2. точки А і В 3. точки А, В і С 4. точки А, В і К |
А) дві Б) чотири В) жодної Г) три Д) одна |
|
Розв’язання завдань 5-7 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань рисунками.
5. Скільки площин можна провести через точки А, В, С, якщо АВ=5 см, ВС=12 см, АС=17 см?
6. Точки А, В, С і D не лежать в одній площині. Доведіть, що прямі АВ і СD не перетинаються.
7. Побудуйте переріз правильного тетраедра площиною, що проходить через бісектрису грані і протилежну цій грані вершину. Обчисліть площу утвореного перерізу, якщо ребро тетраедра дорівнює 5 см.
Варіант – 2
1. Установіть відповідність між геометричними фігурами ( 1 – 4) та кількістю площин (А – Д), які вони визначають.
|
1. пряма і точка, яка лежить на прямій 2. три точки, які не лежать на одній прямій 3. дві точки кола і його центр 4. чотири точки
|
А) жодної площини Б) тільки одна площина В)жодної або одна площина Г) безліч або одна площина Д) безліч площин |
|
2.Встановіть відповідність між многогранниками (1-4) і їхніми діагональними перерізами (А-Д).
|
1. Чотирикутна піраміда. 2. Тетраедр. 3. Куб. 4.Похилий паралелепіпед.
|
А) Паралелограм. Б) Трикутник. В) Квадрат. Г) Прямокутник. Д) Не існує.
|
|
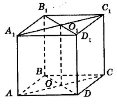
3. Дано зображення прямокутного паралелепіпеда АВСDА1В1С1D1. Установіть відповідність між площинами (1 – 4) та прямими їхнього перетину (А – Д).
|
1. ВВ1 D1 і АВС 2. ВВ1 D1 і АА1С1 3. А1DС і D1С1С 4. В1D1С і АВ1D1
|
А) ОО1 Б) В1D1 В) ВD Г) DС Д) ВD1 |
|
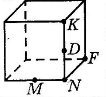4. Скільки граней куба проходить через указані точки? Установіть відповідність між умовою (1 – 4) та відповіддю (А – Д).
|
1. точку F 2. точки K і M 3. точки М, K і F 4. точку М |
А) три Б) жодної В) дві Г) одна Д) чотири |
|
Розв’язання завдань 5-7 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань рисунками.
5. Скільки площин можна провести через точки А, В, С, якщо АВ=5 см, ВС=12 см, АС=13 см?
6. Доведіть, що якщо дві прямі АВ і СD не лежать в одній площині, то прямі АС і ВD також не лежать в одній площині.
7. Дано куб АВСDA1B1C1D1. Побудуйте лінію перетину площин (АD1С) і (A1C1D). Знайдіть довжину відрізка цієї прямої, що знаходиться в середні куба, якщо ребро куба дорівнює 4 см.
-
А можно пожалуйста ответы к контрольной работе? -
про публікацію авторської розробки
Додати розробку