Контрольна робота з алгебри за темою "“ Узагальнення і систематизація навчального матеріалу”

Алгебра, 7 КЛАС

Урок  №  ______                                                                    Дата  ____________

Тема. Контрольна  робота  № 6  за  темою  “Узагальнення  і  систематизація  навчального  матеріалу” 

Мета. Перевірити знання, уміння і навички учнів з курсу алгебри 7 класу; розвивати конкретне мислення, пам´ять; виховувати самостійність, акуратність.

Тип уроку: узагальнення знань та умінь.

Метод: проблемний.

ХІД УРОКУ

І. Оргмомент

ІІ. Контрольна робота  (2 варіанти)

Варіант 1

1. Спростіть вираз:               −3(x + y) − 2(x − y).

2. Обчисліть:   .

3. Розв’яжіть рівняння:          2х + 7 = 17.

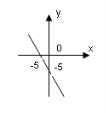4. На якому з малюнків зображено графік рівняння ?

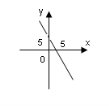
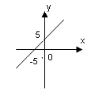
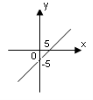А)   Б)   В)   Г)

5. Знайдіть значення функції в точці = −16, =  .

6. Перетворіть вираз у многочлен:  .

7. Розв’яжіть рівняння:       x(4x + 11) − 7(x² − 5x) = 55х.

8. За 3 години  руху за течією і 2 години проти течії теплохід проходить 203 км, а за 2 години за течією і 3 години проти течії – 197 км. Знайдіть швидкість теплохода у стоячій воді.

9*. Якщо довжину прямокутника зменшити на 4 см, а ширину збільшити на 0,5 дм, то одержимо квадрат, площа якого на 40 см² більша ніж площа прямокутника. Знайдіть площу прямокутника.

10*. Один сплав містить 10% цинку, а другий – 30% цинку. Скільки кілограмів кожного сплаву треба взяти, щоб отримати 400 т сплаву, який містить 25% цинку?

Варіант 2

1. Спростіть вираз:    −5(a − 1) + 3(a + 1).

2. Обчисліть:    .

3. Розв’яжіть рівняння:     3х – 5 = 16.

4. На якому з малюнків зображено графік рівняння .

А)   Б)   В)   Г)

5. Знайдіть значення функції в точці = −14, = .

6. Перетворіть вираз у многочлен:  .

7. Розв’яжіть рівняння:    x(2x + 3) − 5(x² − 3x) = − 3x(2x + 2).

8. Із двох міст, відстань між якими 450 км, одночасно  назустріч один одному вирушили два автомобілі і зустрілися через 3 години. Скільки  кілометрів проїхав кожний з них до зустрічі,якщо швидкість одного з них на 10 км/год  більша ніж у другого?

9*. Якщо ширину прямокутника збільшити на 2 дм, а довжину зменшити на 0,5 м, то одержимо квадрат площа якого на 50 дм² менша, ніж площа прямокутника. Знайдіть площу прямокутника.

10*. З двох розчинів солі − 10% і 15% − потрібно отримати 40 г 12% розчину. Скільки для цього потрібно взяти кожного розчину?

Варіант 3*

1. Знайдіть значення виразу:    24,5 − 4m; якщо m = 6.

2. Знайдіть площу поверхні стіни, довжина якої а ширина .

3. Розв’яжіть рівняння:   .

4. Розв’яжіть систему рівнянь: .

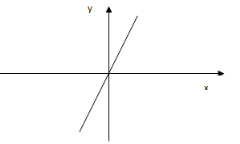
5. Графік якої функції зображено на малюнку?

А) у = х + 3;            Б) у = −2 х;

В) у = х;              Г) у = −3 х.

6. Обчисліть:      .

7. Запишіть у вигляді многочлена:  .

8. За 5 годин руху за течією і дві години проти течії пароплав проходить 181 км, а за дві години за течією і 3 години проти течії – проходить 123 км. Знайдіть власну швидкість пароплава та швидкість течії.

9*. Якщо довжину прямокутника зменшити на 4 см, а ширину збільшити на 0,5 дм, то одержимо квадрат, площа якого на 40 см² більша ніж площа прямокутника. Знайдіть площу прямокутника.

10*. Один сплав містить 30% міді, а другий – 70% міді. Скільки кілограмів кожного сплаву треба взяти, щоб отримати 100 кг сплаву, який містить 40% міді?