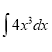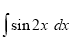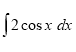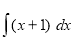Контрольна робота з математики за 11 клас.

Варіант 1

Завдання 1- 20 мають по п’ять варіантів відповіді, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей

1 Обчисліть значення виразу .

А)-2; Б) 125; В) 1/2; Г)-1/2. Д)3

2 Розв’яжіть нерівність 3^2x+4 > 9.

А) (—1; +∞); Б) (—∞; —1); В)(-1/2;+∞); Г)(-∞;-1/2). Д)3

3 Знайдіть значення виразу х² - 4х + 4 при х= 2 + .

А) 3; Б) ; В) 6; Г) 2 . Д)3

4 Скоротіть дріб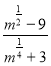

А) ; Б); В) ; Г) . Д)3

5 Укажіть точку перетину графіка функції f(x)= lg(x - 2) з віссю абсцис. А) А (2; 0); Б) В (0; 2); В)С(3;0); Г)D(0;3). Д)3

6 Спростіть вираз cos(π/2 - а) + sin (л + а).

A)sinа + cosа; Б) 2cosа; В) 2sinа; Г) 0. Д)3

7 Яке число треба додати до числа 10, щоб отримана сума відносилася до числа 12, як число 28 відноситься до числа 24?

А)2; Б) 3; В) 4; Г)8 Д)3

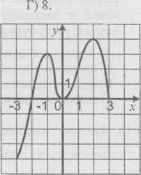
8 Функція v = f(х) , графік якої зображено на

рисунку, визначена на проміжку [-3; 3]. Укажіть множину значень аргументу функції, при яких f'(х) > 0.

А) (-2; 0)U(0; 3);    В) [-2; 3];

Б) [—3; — 1]U[0; 2];    Г) (-1; 0)U(2; 3]. Д)3

9 Укажіть загальний вигляд первісних функції f(x) = 10x⁴ – 6x.

А) 2х⁵ -Зх² + С;

Б) 2х⁵ -4х² + С ; Г)40x³-6 + С. Д)3

10 Графік якої функції симетричний графіку функції у = відносно осі ординат?

А )у = Б )у = - В) = - ; Г)у = . Д)3

11 Яке число є періодом функції у = sin2х ?

А)-π/2  Б) π/4  В)π ; Г) π/2 Д)3

12 Поспіль двічі підкидають гральний кубик. Яка ймовірність того, що обидва рази випаде 6 очок?

А)1/6  Б) 1/12  В)1/72; Г) 1/36 Д)3

13 Яка функція є спадною?

А) у = 8x; Б) у = -8/x; В) у = -8x; Г) у = 8^х. Д) у = 3

14 Відомо, що 5^x : 5^у = 125 . Чому дорівнює значення виразу х-у ?

А) 0; Б) 1; В) 2; Г) 3. Д)3

15 Знайдіть значення виразу .

А) 54; Б) 36; В) 18; Г) 72. Д)3

16 Розв’яжіть нерівність log₂(x - 3) < 3 .

А) (-∞; 11); Б) (-∞; 5); В) (3; 11); Г) (3; 12). Д)3

17 У трикутнику АВС відомо, що <C=90°, AС=3 см, BС=18 см. Знайдіть tgА.

А)1/6  Б) 6; В) 9; Г)1/9 Д)3

18 Площа прямокутника АВСD, зображеного на рисунку, дорівнює 12 см². Чому дорівнює площа трикутника АОВ

А)2cm²   В) 3 см²;

Б) 4cm²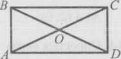  Г) знайти неможливо . Д)3

19 Сторона АС трикутника АВС, зображеного на рисунку, належить площині а, точки M і K — середини сторін АВ і ВС трикутника відповідно, точка В знаходиться поза площиною а. Яке взаємне розташування прямої МК і площини а?

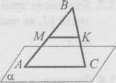A) пряма і площина перетинаються;

Б) пряма і площина паралельні;

B) пряма належить площині;

Г) встановити неможливо. Д) пряма не належить площині;

20 При яких значеннях т і п вектори а (10; т; 5) і b (2; 3; п) колінеарні?

 А) т = 3, п = 5 ; Б) т = 10, п = 2 ; В) т - 12, п = 3 ; Г) т = 15, п = 1. Д) т = 17, п = 1.

 

У завданнях 21 -24 до кожного з чотирьох рядків інформації, позначених цифрами, доберіть один правильний, на Вашу думку, варіант, позначений буквою

 

21. Установити відповідність між виразами (1-4) та тотожно рівними їм виразами (А-Д).

1	x2-(x-1)(x + 3)	А	2х + 3
2	x2-(x+1)(x+3)	Б	4x-3
3	х2-(х- 1)(х - 3)	В	-4x-3
4	x2-(x+1)(x-3)	Г	-4x + 3
		Д	-2х + 3

22.Установити відповідність між інтегралами (1-4) та їхніми значеннями (А-Д).

1		А	-1/2cosx+c
2		Б	2sinx+c
3		В	x2/2+x+c
4		Г	x4/4+c
		Д	2x+c

 

23.Установити відповідність між елементами (1-4) рівностороннього трикутника зі стороною а та їхніми величинами (А-Д).

1	Висота	А
2	Радіус вписаного кола	Б
3	Кут між медіанами	В	300
4	Радіус описаного кола	Г	600
		Д

24. Установити відповідність між геометричними тілами (1-4) та формулами для відшукання їх об’ємів (А-Д).

1	Циліндр	А	πr2H
2	Куля	Б	πrl
3	Конус	В	πr2H/3
4	Піраміда	Г	4πr3/3
		Д	SоснH/3

 

Розв’яжіть завдання 25 – 28. Одержані числові відповіді запишіть у екзаменаційну роботу.

25.Знайдіть значення похідної функції f(x) = ln³ х у точці х₀ =e.

26. Обчисліть інтеграл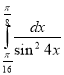

27. Бічна сторона рівнобедреного трикутника відноситься до його основи як 5:6, а висота трикутника, опущена на основу, дорівнює  12 см. Обчисліть периметр трикутника.

28. Основа прямої призми — прямокутний трикутник із катетом 6 см і гострим кутом 45°. Об'єм призми дорівнює 108 см³. Знайдіть площу бічної поверхні призми.

 

Розв’яжіть завдання 29 –30. Запишіть послідовні логічні дії та пояснення всіх етапів розв’язання завдань, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань рисунками, графіками тощо.

 

29. Розв’яжіть рівняння:1оg₅(5^x -4) = 1-х.

30.Через сторону квадрата проведено площину, яка утворює з площиною квадрата кут 45°. Знайдіть кут між діагоналлю квадрата і цією площиною.