Контрольна робота з теми "Лінійні рівняння з однією змінною. Розв’язування задач за допомогою рівнянь"

Контрольна робота № 1

Лінійні рівняння  з однією змінною. Розв’язування задач за допомогою рівнянь.

І Варіант

1. Яке з рівнянь лінійне

2. Яке з рівнянь є рівносильним даному 2х – 8 = 5 + 4х:

3.     Коренем якого лінійного рівняння число 13?

4.    Коренем лінійного рівняння 2х – 10 = х число:

5.   Скільки коренів має рівняння 17х = 17

6.   Яке рівняння відповідає умові задачі:

 Сума двох натуральних чисел дорівнює 53. Одне число більше від другого на  13. Знайти менше число.

7.    Установіть відповідність між рівняннями (1 – 4) й числами, які є коренями цих        рівнянь (А-Д).

     1)  -х + 2 = -3                     А      -1        

     2)  3х + 4 = - х                   Б      - 5

     3)  2х = 15+5х                   В      - 4

     4)  -3 (2 + х) = 2 – х          Г       5

                                               Д      4

8.  Розв’язати рівняння:   5(х – 2) + 3 х = 2х – (10 – 6х).   

9.  Розв’язати задачу: У двох контейнерах було порівну яблук. Коли з першого контейнера взяли 13 кг яблук, а з другого – 31 кг, то в другому контейнері залишилось у 3 рази менше яблук, ніж у першому. Скільки яблук було в кожному контейнері спочатку?

10. Розв’язати рівняння: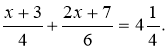       

11. Розв’язати задачу: Човен плив 2,8 год за течією річки та 3,4 год проти течії. За течією човен пройшов на 4,4 км менше, ніж проти течії. Знайти швидкість човна в стоячій воді, якщо швидкість течії річки дорівнює 2 км/год?

ІІ Варіант

1. Яке з рівнянь лінійне:

2. Яке з рівнянь є рівносильним даному 5х + 7 = 17 – 9х:

3. Коренем  якого лінійного рівняння число 11?

4. Чи є коренем лінійного рівняння 3х – 18 = х число:

5. Скільки коренів має рівняння 0 ∙ х = 0?

6. Яке рівняння відповідає умові задачі:

Сума двох натуральних чисел дорівнює 50. Одне число більше від іншого на 18. Знайти менше число.

7.  Установіть відповідність між рівняннями (1 – 4) й числами, які є коренями  цих рівнянь (А-Д).

      1)  3х + 4 = -5                     А     3        

      2)  – х – 1 = 2 х                   Б     2

      3)  – 5 х = -2 - 4х                 В     - 3

      4)  2 (1 – х) = х – 7              Г    - 2

                                                   Д     -

8. Розв’язати рівняння:    2(х – 6) + 4 х = 5х – (8 – х).

9. Розв’язати задачу:  На двох полицях стояло порівну книжок. Коли з першої полиці взяли 3 книжки, а з другої – 14, то на першій полиці залишилось у 2 рази більше книжок, ніж на другій. Скільки книжок було на кожній полиці спочатку?

10.  Розв’язати рівняння:       

11.  Розв’язати задачу: Човен плив 2,4 год за течією річки та 0,8 год проти течії. За течією човен пройшов на 19,2 км більше, ніж проти течії. Знайти швидкість човна в стоячій воді, якщо швидкість течії річки дорівнює 3 км/год?