Контрольна робота "Застосування інтеграла"

Про матеріал

Контрольна робота "Застосування інтеграла" в двох варіантах, складається з двох частин: 1 частина - тестові завдання, вибрані із збірників для ЗНО, 2 частина - диференційовані завдання: для учнів 1 - 2 рівнів (мах 7 балів) та для для учнів 3 - 4 рівнів (мах 12б.)

Перегляд файлу

Контрольна робота №

Тема «Застосування інтеграла»

В – 1

1 частина

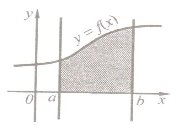
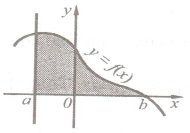
1. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\КР1\КР1 005.jpg$
Б) S = – dx
В) S = – dx
Г) S = dx
Д) S = dx

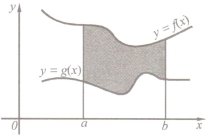
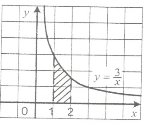
2. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\КР1\КР1 006.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

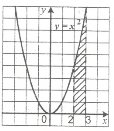
3. Обчислити площу заштрихованої фігури:

А) S =19	$C:\Users\Lenovo\Desktop\КР1\КР1 003.jpg$
Б) S = 10
В) S = 1
Г) S = 6
Д) S = 6

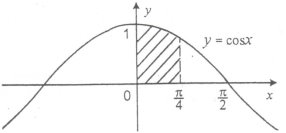
4. Обчислити площу заштрихованої фігури:

А) S =1	$C:\Users\Lenovo\Desktop\КР1\КР1 001.jpg$
Б) S =
В) S =
Г) S =
Д) S =

5. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом V= (2t – 1)м/с. Знайдіть шлях (у метрах), який проходить тіло за інтервал часу від t₁ = 1с до t₂= 3с.

А) 5м; Б) 4м; В) 8м; Г) 6м; Д) 7м.

2 частина

1 – 2 рівні	3 – 4 рівні
6. Знайти площу фігури, обмеженої графіками:
а) у = – х + 3, х = 2, х = – 1, у = 0. б) у = , х = 0, х =	а) у = – 2х + 1, х = – 1, х = 3. б) у = 2х², у = 6х – х².
7. Обчислити об’єм тіла, що обертається навколо осі ОХ та обмежене:
а) у = , х = 1, х = 4. б) у = х + 2, х = 0, х = 3.	а) у = х² – 1, х = – 1, х = 1. б) у = , х = 0, х = .

Контрольна робота №

Тема «Застосування інтеграла»

В – 2

1 частина

1. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\КР1\КР1 005 — копия.jpg$
Б) S = – dx
В) S = – dx
Г) S = dx
Д) S = dx

2. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\КР1\КР1 006.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = ) dx

3. Обчислити площу заштрихованої фігури:

А) S = 3	$C:\Users\Lenovo\Desktop\КР1\КР1 004.jpg$
Б) S = 3
В) S =
Г) S = – 3
Д) S = – 3

4. Обчислити площу заштрихованої фігури:

А) S =1	$C:\Users\Lenovo\Desktop\КР1\КР1 001.jpg$
Б) S =
В) S =
Г) S =
Д) S =

5. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом V= (4t – 1)м/с. Знайдіть шлях (у метрах), який проходить тіло за інтервал часу від t₁ = 1с до t₂= 3с.

А) 10м; Б) 14м; В) 16м; Г) 13м; Д) 8м.

2 частина

1 – 2 рівні	3 – 4 рівні
6. Знайти площу фігури, обмеженої графіками:
а) у = – х + 3, х = 2, х = – 1, у = 0. б) у = , х = 0, х =	а) у = – 2х + 1, х = – 1, х = 3. б) у = 2х², у = 6х – х².
7. Обчислити об’єм тіла, що обертається навколо осі ОХ та обмежене:
а) у = , х = 1, х = 4. б) у = х + 2, х = 0, х = 3.	а) у = х² – 1, х = – 1, х = 1. б) у = , х = 0, х = .

docx

Завантажити

Зберегти на потім

Додав(-ла)

Юрійчук Ярослава Миколаївна

Пов’язані теми

Алгебра, 11 клас, Контрольні роботи

До підручника

Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)

До уроку

25.2. Обчислення площ і об’ємів за допомогою визначених інтегралів

Додано

11 березня 2019

Переглядів

2496

Оцінка розробки

Відгуки відсутні